Propiedades de los radicales: qué son y ejemplos

¿Qué son las propiedades de los radicales?

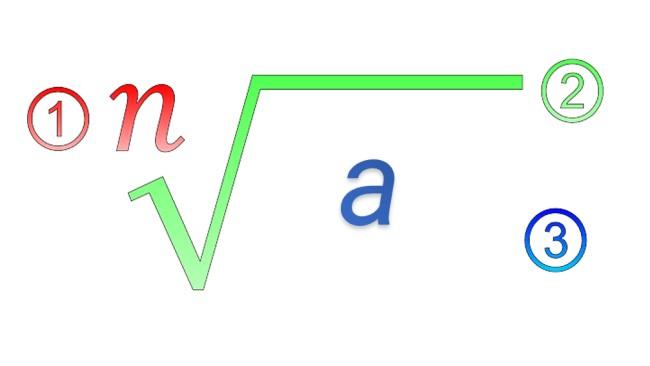
Las propiedades de los radicales son operaciones que permiten solucionar problemas complejos de radicales y potencias. El radical es la forma de simbolizar matemáticamente a la raíz n-ésima de una cantidad “a”. Dicha raíz es otra cantidad, llamada “b”, tal que su potencia n-ésima es precisamente “a”, de modo que es válido escribir lo siguiente:

El valor de “n” es un número natural, el cual se conoce como el índice de la raíz, “a” es el radicando o  cantidad subradical, y “b” es la raíz n-ésima de “a”. Tanto “a” como “b” pertenecen al conjunto de los números reales.

Si en un radical no se escribe el índice, se entiende de inmediato que su valor es igual a 2 y se lee “raíz cuadrada de a”.

Dado que “n” pertenece al conjunto de los números naturales, puede tratarse de un número par o impar. Entonces, se distinguen los siguientes casos:

Para “n” par

• Si a > 0 o igual a 0, la raíz n-ésima de “a” es positiva o 0, y recibe el nombre de raíz principal.
• Cuando a 0, no existe raíz n-ésima en el conjunto de los números reales, pero sí en los números complejos.

Para “n” impar

• Si a > 0, la raíz n-ésima de “a” es positiva.
• Cuando a 0, la raíz n-ésima de “a” es negativa.

Algunos ejemplos son los siguientes:

Propiedades de la radicación

Es posible escribir la raíz n-ésima de una cantidad como una potencia con exponente fraccionario, es decir, un número racional.

En este caso, el índice de la raíz pasa a ser el denominador, mientras que el exponente de la cantidad subradical se convierte en el numerador:

Expresión que es válida siempre y cuando n ≠ 0, ya que no se admiten fracciones con denominador nulo.

De esta forma, las mismas propiedades que se aplican a las potencias, pueden utilizarse en el caso de los radicales.

Para valores pertenecientes al conjunto de los números reales, dichas propiedades son las siguientes:

1. Producto de radicales de igual índice

En el producto de dos (o más) radicales del mismo índice, se multiplican las cantidades subradicales, manteniendo el índice:

2. Cociente de radicales de igual índice

El cociente entre la raíz n-ésima de “a” y la raíz n-ésima de “b”, siendo b ≠ 0, es igual a la raíz n-ésima del cociente entre “a” y “b”:

3. Raíz de raíz

Para hallar la raíz n-ésima de la raíz m-ésima de la cantidad “a”, se escribe la cantidad subradical bajo una raíz cuyo índice es el producto entre “n” y “m”:

El procedimiento se extiende fácilmente a sucesivas raíces anidadas. El índice de la raíz resultante, es el producto de todos los índices, así:

4. Potencia de una raíz

Una raíz n-ésima, elevada a la potencia m, se expresa elevando la cantidad subradical a dicha potencia:

Casos particulares:

1) Si n = m, el signo de raíz desparece, quedando la base elevada a la potencia 1:

Lo cual es válido para a ≥ 0. En general, si el índice de la raíz es un número par, se tiene:

(Ver ejemplos más adelante)

2) Si m > n, la fracción m/n es impropia y la raíz se puede simplificar, por ejemplo, buscando la fracción equivalente a m/n tal que el numerador y el denominador sean primos entre sí, o reescribiendo la cantidad subradical y aplicando alguna de las propiedades descritas acá.

(Ver ejemplos más adelante)

5. Amplificación de radicales

Un radical puede amplificarse por un factor q, si tanto el índice de la raíz, como la potencia de la cantidad subradical se multiplican por dicho factor, y esta operación no conlleva la modificación del resultado. Por lo tanto:

Siempre que a ≥ 0 cuando q sea par.

6. Introducción de un factor dentro de un radical

Si un factor positivo “b” se encuentra multiplicando a un radical, puede pasar dentro de este, si se eleva al mismo índice de la raíz. En tal caso:

7. Suma y resta de radicales

Los radicales pueden sumarse y restarse, siempre y cuando sean del mismo índice y tengan la misma cantidad subradical.

Cuando dos o más radicales son de igual índice y cantidad subradical, se dice que son radicales semejantes.

Por ejemplo, los siguientes radicales son semejantes:

En cambio, estos radicales no son semejantes, porque no tienen la misma cantidad subradical:

Tampoco son semejantes estos dos:

Ya que el índice del radical no es el mismo.

Los radicales semejantes pueden reducirse a uno solo, sumando o restando los coeficientes que los acompañan.

Ejemplos de propiedades de radicales

Ejemplo 1

¿Cuál es el valor de las siguientes raíces?

La raíz cuadrada de 32 se puede encontrar directamente con la ayuda de la calculadora. Su valor es:

Los puntos suspensivos indican que existen infinitos decimales, además se trata de un número irracional, pues no se puede escribir en forma de fracción.

Si se prefiere no trabajar con números decimales, la raíz cuadrada de 32 también puede calcularse descomponiendo 32 en sus factores primos:

32 = 2⁵

De esta forma, al sustituir, se obtiene:

Escrito como exponente fraccionario:

La fracción 5/2 es impropia, por lo que el radical se puede simplificar, haciendo uso de las propiedades de las potencias:

Aplicando ahora la propiedad 1 anteriormente descrita:

Por lo tanto:

Por su parte:

Ya que (−2)³ = −8.

De acuerdo a la propiedad 4:

Y, por último, la raíz cuadrada de −8 no existe en el conjunto de los números reales, aunque sí en el de los números complejos.

Ejemplo 2

Dada la siguiente operación:

¿Es posible reducir el resultado?

Siempre que los radicales sean semejantes, es posible reducirlos, pero para ello deben tener el mismo índice e igual cantidad subradical. En el ejemplo anterior se vio que:

Un procedimiento análogo se puede emplear para escribir el primer sumando, de tal forma que la cantidad subradical sea igual a 2:

Este radical es semejante al anterior. En cuanto a la raíz cuadrada de 81, esta es 9, por lo tanto:

Ejemplo 3

¿Qué propiedades es necesario aplicar para efectuar esta operación?

Hay que aplicar las propiedades 3 y 5, que son, respectivamente, raíz de una raíz e introducción de un valor en un radical. En primer lugar, se aplica la propiedad 5, para introducir la “x” que está fuera de la raíz más interna:

Y ahora la expresión está lista para aplicar la propiedad 3, y multiplicar los respectivos índices de cada radical:

Referencias

1. Gonzáles, D. 2011. Álgebra Básica: Teoría y Práctica. 2da. Edición.
2. Haeussler, E. 2012. Precálculo. 1ra. Edición. Pearson.
3. Khan Acadaemy. Exponents and Radicals. Recuperado de: khanacademy.org.
4. Larson, R. 2012. Precálculo. 8va. Edición. Cengage Learning.
5. Stewart, J. 2007. Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.