Prueba U de Mann - Whitney: qué es y cuándo se aplica, ejecución, ejemplo
La prueba U de Mann – Whitney se aplica para la comparación de dos muestras independientes cuando las mismas tienen pocos datos o no siguen una distribución normal. De esta manera, se considera que es una prueba no paramétrica, a diferencia de su homóloga la prueba t de Student, que se usa cuando la muestra es suficientemente grande y sigue la distribución normal.
Frank Wilcoxon la propone por primera vez en 1945, para muestras de tamaños idénticos, pero dos años después fue extendida para el caso de muestras de distinto tamaño por Henry Mann y D. R. Whitney.
Con frecuencia la prueba se aplica para comprobar si existe relación entre una variable cualitativa y otra cuantitativa.
Un ejemplo ilustrativo es tomar un conjunto de personas hipertensas y extraer dos grupos, a quienes se le registran los datos de tensión arterial diaria durante un mes.
A un grupo se le aplica el tratamiento A y a otro el tratamiento B. Aquí la tensión arterial es la variable cuantitativa y el tipo de tratamiento es la cualitativa.
Se quiere saber si la mediana, y no la media, de los valores medidos es estadísticamente igual o diferente, para establecer si hay diferencia entre ambos tratamientos. Para obtener la respuesta se aplica el estadístico de Wilcoxon o prueba U de Mann – Whitney.
Índice del artículo
- 1 Planteamiento del problema en la prueba U de Mann – Whitney
- 2 Características de la prueba U de Mann Whitney
- 3 Ejemplo práctico de aplicación
- 4 Calculadoras en línea para la prueba U de Mann – Whitney
- 5 Referencias
Otro ejemplo en el cual se puede aplicar la prueba es el siguiente:
Supongamos que se quiere saber si el consumo de bebidas gaseosas difiere en forma significativa en dos regiones del país.
A una de ellas se le llama región A y a la otra región B. Se lleva un registro de los litros consumidos semanalmente en dos muestras: una de 10 personas para la región A y otra de 5 personas para la región B.
Los datos son los siguientes:
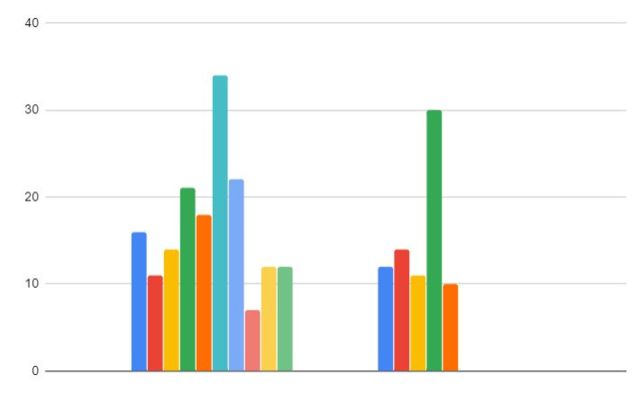
-Región A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12
-Región B: 12,14, 11, 30, 10
Se plantea la siguiente interrogante:
¿El consumo de bebidas gaseosas (Y) depende de la región (X)?
-Variable cualitativa X: Región
-Variable cuantitativa Y: Consumo de gaseosas
Si la cantidad de litros consumidos es igual en ambas regiones, la conclusión será que no hay dependencia entre las dos variables. La manera de saberlo es comparar la tendencia media o mediana para las dos regiones.
Caso normal
Si los datos siguieran una distribución normal se plantean dos hipótesis: la nula H0 y la alternativa H1 a través de la comparación entre las medias:
–H0: no hay diferencia entre la media de las dos regiones.
–H1: las medias de ambas regiones son distintas.
Caso con tendencia no – normal
Por el contrario, si los datos no siguen una distribución normal o simplemente la muestra es muy pequeña para poder saberlo, en vez de comparar la media se compararía la mediana de las dos regiones.
–H0: no hay diferencia entre la mediana de las dos regiones.
–H1: las medianas de ambas regiones son distintas.
Si las medianas coinciden, entonces se cumple la hipótesis nula: no hay relación entre consumo de gaseosas y la región.
Y si sucede lo contrario, es cierta la hipótesis alternativa: sí hay relación entre consumo y región.
Es para estos casos donde es indicada la prueba U de Mann – Whitney.
Muestras apareadas o no apareadas
La siguiente cuestión importante para decidir si se aplica la prueba U de Mann Whitney, es si el número de datos en ambas muestras es idéntico, lo que equivale a decir que están a la par.
Si las dos muestras están apareadas se aplicaría la versión original de Wilcoxon. Pero si no, como es el caso del ejemplo, entonces se aplica la prueba de Wilcoxon modificada, que es precisamente la prueba U de Mann Whitney.
La prueba U de Mann – Whitney un test no-paramétrico, aplicable a muestras que no siguen la distribución normal o con pocos datos. Tiene las siguientes características:
1.- Compara las medianas
2.- Funciona sobre rangos ordenados
3.- Es menos potente, entendiéndose por potencia la probabilidad de rechazar la hipótesis nula cuando en realidad es falsa.
Tomando en cuenta estas características, la prueba U de Mann – Whitney se aplica cuando:
-Los datos son independientes
-No siguen la distribución normal
-La hipótesis nula H0 se acepta si las medianas de las dos muestras coinciden: Ma = Mb
-Se acepta la hipótesis alternativa H1 si las medianas de las dos muestras difieren: Ma ≠ Mb
La variable U es el estadígrafo de contraste usado en la prueba de Mann – Whitney y se define así:
U = min(Ua, Ub)
Esto significa que U es el menor de los valores entre Ua y Ub, aplicada a cada grupo. En nuestro ejemplo sería a cada región: A o B.
Las variables Ua y Ub se definen y se calculan de acuerdo a la siguiente fórmula:
Ua = Na Nb + Na(Na +1)/2 – Ra
Ub = Na Nb + Nb(Nb +1)/2 – Rb
Aquí los valores Na y Nb son los tamaños de las muestras correspondientes a las regiones A y B respectivamente y por su parte, Ra y Rb son las sumas de rango que definiremos más abajo.
1.- Ordenar los valores de las dos muestras.
2.- Asignar un rango de orden a cada valor.
3.- Corregir las ligaduras existentes en los datos (valores repetidos).
4.- Calcular Ra = Sumatoria de los rangos de la muestra A.
5.- Hallar Rb = Sumatoria de los rangos de la muestra B.
6.- Determinar el valor Ua y Ub, de acuerdo a las fórmulas dadas en el apartado anterior.
7.- Comparar Ua y Ub, y se asigna el menor de los dos al estadístico U experimental (es decir de los datos) que se compara con el estadístico U teórico o normal.
Ahora aplicamos lo antes dicho al problema de las gaseosas planteado previamente:
Región A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12
Región B: 12,14, 11, 30, 10
Dependiendo que las medias de ambas muestras sean estadísticamente iguales o diferentes se procede a aceptar o rechazar la hipótesis nula: no hay relación entre las variable Y y X, es decir el consumo de gaseosas no depende de la región:
H0: Ma = Mb
H1: Ma ≠ Mb
Procedemos a ordenar los datos en forma conjunta para las dos muestras, ordenando los valores de menor a mayor:

Observe que el valor 11 aparece 2 veces (una vez en cada muestra). Originalmente tiene posiciones o rangos 3 y 4, pero para no sobrestimar o subestimar uno o el otro se elige como rango el valor medio, es decir 3,5.
En forma semejante se procede con el valor 12, que se repite tres veces con rangos 5, 6 y 7.
Pues al valor 12 se le asigna el rango promedio de 6 = (5+6+7)/3. Y lo mismo para el valor 14, que tiene ligadura (aparece en ambas muestras) en las posiciones 8 y 9, se le asigna el rango promedio 8.5 = (8+9)/2.
A continuación se separan nuevamente los datos para la Región A y B pero ahora se les asigna en otra fila sus rangos correspondientes:
Región A

Región B

Los rangos Ra y Rb se obtienen de las sumas de los elementos de la segunda fila para cada caso o región.
Se calculan los respectivos valores Ua y Ub:
Ua = 10×5 + 10(10+1)/2 – 86 = 19
Ub = 10×5 + 5(5+1)/2 -34 = 31
Valor experimental U = min(19, 31) = 19
Se supone que el U teórico sigue una distribución normal N con parámetros dados exclusivamente por el tamaño de las muestras:
N( (na⋅nb)/2 , √[ na nb (na + nb +1) /12 ] )
Para poder comparar la variable U obtenida experimentalmente, con la U teórica es necesario hacer un cambio de variable. Se pasa de la variable U experimental a la su valor tipificado, el cual se llamará Z, con la finalidad de poder hacer la comparación con el de una distribución normal tipificada.
El cambio de variable es el siguiente:
Z= (U – na.nb / 2) / √[na. nb (na + nb + 1) / 12]
Debe notarse que para el cambio de variable se usaron los parámetros de la distribución teórica para U. Entonces la nueva variable Z, que es un híbrido entre la U teórica y la U experimental, se contrasta con una distribución normal tipificada N(0,1).
Criterio de comparación
Si Z ≤ Zα ⇒ se acepta la hipótesis nula H0
Si Z > Zα ⇒ se rechaza la hipótesis nula H0
Los valores críticos Zα tipificados dependen del nivel de confianza requerido, por ejemplo para un nivel de confianza α=0,95 = 95% que es lo más usual se tiene el valor crítico Zα = 1,96.
Para los datos mostrados acá:
Z= (U – na nb / 2) / √[na nb (na + nb + 1) / 12] = -0,73
El cual está por debajo del valor crítico 1,96.
Entonces la conclusión final es que se acepta la hipótesis nula H0:
No hay diferencia en el consumo de gaseosas entre las regiones A y B.
Existen programas específicos para cálculos estadísticos, entre ellos destacan SPSS y MINITAB, pero estos programas son de pago y su uso no siempre es sencillo. Ello se debe a que dan tantas opciones, que prácticamente su uso queda reservado a los expertos en Estadística.
Afortunadamente, existen varios programas en línea muy precisos, gratuitos y de uso sencillo que permiten ejecutar entre otras la prueba U de Mann – Whitney.
Estos programas son:
-Social Science Statistics (socscistatistics.com), el cual posee tanto la prueba U de Mann- Whitney como la de Wilcoxon para el caso de muestras balanceadas o apareadas.
-AI Therapy Statistics (ai-therapy.com), que posee varias de las pruebas usuales de la estadística descriptiva.
-Statistic to Use (physics.csbsju.edu/stats), una de las más antiguas, por lo que su interfaz puede lucir anticuada, aunque sin embargo es un programa gratuito muy eficiente.
- Dietrichson. Métodos cuantitativos: prueba de los rangos. Recuperado de: bookdown.org
- Marín J P. Guía SPSS: Análisis y procedimientos en pruebas no paramétricas. Recuperado de: halweb.uc3m.es
- USAL MOOC. Test no paramétricos: U de Mann – Whitney. Recuperado de: youtube.com
- Wikipedia. Prueba U de Mann – Whitney. Recuperado de: es.wikipedia.com
- XLSTAT. Centro de ayuda. Tutorial de prueba de Mann – Whitney en Excel. Recuperado de: help.xlsat.com
