Estimación por intervalos: qué es, ejemplos y ejercicios resueltos
¿Qué es la estimación por intervalos?
La estimación por intervalos es la forma de determinar el rango de valores en los que puede estar comprendida la media poblacional, a partir de la información de una muestra de tamaño finito, extraída aleatoriamente de la población total.
El intervalo de estimación es menor en la medida que la muestra es de mayor tamaño, pero se hace más amplio si aumenta el nivel o porcentaje de confiabilidad del mismo.
Si se quisiera conocer la media poblacional de cierta variable en forma exacta, entonces habría que considerar la población total, algo que no siempre es factible, ya que si se trata de una población muy grande, resulta costoso conseguir los datos de toda la población. Por este motivo se recurre a la toma de una o varias muestras aleatorias de la población total.
Se parte de la hipótesis de que, al extraer una muestra aleatoria, no sesgada y tomando en consideración de forma proporcional todos los estratos, entonces el valor medio de la muestra tiene que ser muy cercano al de la media poblacional.
La lógica indica que cuanto mayor es el número de datos de la muestra, la diferencia entre el valor medio muestral y el valor medio poblacional es menor.
Intervalo de estimación
En la práctica, a menos que se conozca la población completa, solo es posible encontrar, con cierta probabilidad, el intervalo donde puede hallarse la media poblacional, partiendo de una muestra de tamaño finito.
En el caso de una población que siga una distribución normal, con desviación estándar σ , la diferencia estándar entre el promedio poblacional μ y el promedio
|μ –
Aquí, la palabra “estándar” indica que el 68% de las muestras de tamaño n, tienen valor medio
Estimación estándar
Una interpretación alternativa de lo anterior, sería decir que la media poblacional obtenida a partir de una muestra de tamaño n y valor medio
En la mayoría de los casos reales, no es posible conocer la desviación estándar poblacional, por lo que σ se aproxima mediante la desviación estándar de la muestra s, que se calcula de la siguiente manera:
s = √(∑(xi –
De allí se obtiene el intervalo que podría contener a la media poblacional con un nivel de confianza del 68% (nivel de confianza estándar), dado por:
A ese intervalo de estimación de la medida poblacional se le conoce como intervalo de estimación estándar y fue obtenido únicamente con los datos de la muestra disponible de tamaño n.
De la fórmula anterior se deduce que, si se quisiera estrechar el intervalo de estimación a la mitad, es necesario cuadruplicar el tamaño de la muestra.
Estimación por intervalos de confianza
En determinados estudios, un nivel de confianza estándar del 68% puede ser insuficiente, entonces se requiere determinar los intervalos con un nivel de confianza arbitrario γ.
Si denotamos por ε el error estándar s/√n, entonces el error de estimación para un nivel de confianza γ estará dado por:
E = Zγ⋅ε.
Donde Zγ es un número por el que se multiplica el error estándar, y obtener así el margen de error con un nivel de confianza arbitrario γ.
Para obtener el factor Zγ, se procede de la siguiente manera:
Paso 1
Se encuentra el llamado nivel de significancia α correspondiente al nivel de confianza γ mediante la siguiente fórmula:
α = 1 – γ
Paso 2
Se determina el valor:
Paso 3
Se despeja Zγ la ecuación:
N(Zγ) = 1 – α/2
Como se trata de una ecuación integral, este despeje se obtiene a partir de las tablas de la distribución normal, usando el método de interpolación lineal.
Paso 4
Alternativamente al uso de tablas, pueden usarse las funciones estadísticas incorporadas en las hojas de cálculo como Excel, o Google Sheet. Estos programas incorporan la función normal inversa N-1, de modo que el factor de corrección Zγ se obtiene directamente evaluando sobre dicha función inversa:
Zγ = N-1(1 – α/2).
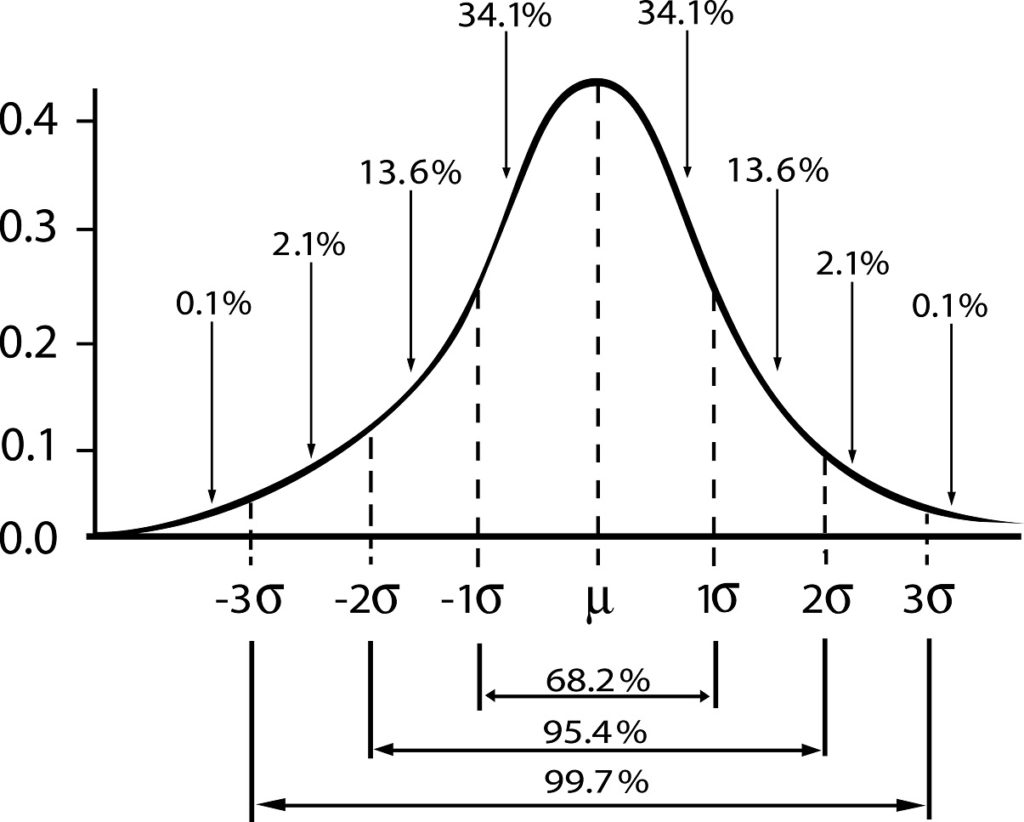
Intervalos de confianza típicos
Los niveles de confianza más frecuentemente usados son:
- Zγ = 1; nivel estándar de confianza γ = 0,68.
- Zγ = 2; nivel de confianza γ = 0,95 (o nivel de significancia 5%).
- Zγ = 3; nivel de confianza γ = 0,997 (o nivel de significancia 0,3%)
Ejemplos
Ejemplo 1
Determinar el intervalo del peso promedio de los recién nacidos durante el mes de agosto en una gran ciudad partiendo de una muestra aleatoria de 100 bebés, en las que se obtuvo un peso promedio de 3100 gramos con una desviación estándar muestral s = 1500 gramos.
Solución
En primer lugar, se determina el error estándar de la muestra:
ε = s/√n = (1500 g)/√100 = 150 g.
Por lo tanto, partiendo de esta muestra se puede inferir que el peso promedio de los bebés nacidos en el mes de agosto en esa ciudad, está comprendido entre 2950 g y 3250 g, con 68% de probabilidad.
Ejemplo 2
Supongamos que se duplica el tamaño de la muestra de bebés nacidos en el mismo mes de agosto y en la misma ciudad del ejemplo 1. El peso promedio de la muestra es 3100 g con una dispersión estándar de 1500 g.
Se pide estimar el intervalo de peso promedio de los recién nacidos de esa ciudad, a partir de esta nueva muestra.
Solución
Ahora el error estándar disminuye en el factor 1/√2, por lo que el nuevo error estándar del peso promedio será 106 g.
Entonces se puede estimar, a partir de esta nueva muestra que, el peso promedio de los recién nacidos está comprendido en el rango que va de los 2994 g a 3206 g, con una probabilidad del 68%.
Ejercicios
Ejercicio 1
Determinar el rango de peso promedio de los recién nacidos en agosto, partiendo de la muestra especificada en el ejemplo 1, con una probabilidad del 95%.
Solución
Un nivel de confiabilidad de 95% duplica el rango del peso promedio, respecto a un nivel de confiabilidad del 68%.
Por tanto, el peso promedio de los recién nacidos está comprendido en el rango de 2800 gramos a 3400 gramos con un 95% de certeza.
Ejercicio 2
Estimar con un nivel de confianza del 99,7% el intervalo en el que se encontrará el peso promedio de los recién nacidos de una gran ciudad, si se dispone de una muestra con el peso promedio de 100 bebés igual a 3100 g, y con una desviación estándar muestral s= 1500 g.
Solución
El margen de error del peso promedio, con un 99,7% de certeza, será el triple del error del promedio, es decir:
3*1500/√100.
Entonces se infiere, a partir de esta muestra, que el peso promedio los recién nacidos estará comprendido en el intervalo: 2650 gramos a 3550 gramos, con un nivel de certeza del 99,7%.
De este resultado se observa como con un nivel de certeza mayor aumenta la incertidumbre del peso promedio a un intervalo mucho más amplio.
