Variables estadísticas: definición, tipos y ejemplos
¿Qué son las variables estadísticas?
Las variables estadísticas son características que poseen las personas, cosas o lugares y que pueden ser medidas. Ejemplos de variables de uso frecuente son la edad, el peso, la estatura, el sexo, el estado civil, el nivel académico, la temperatura, el número de horas que dura un bombillo incandescente y muchas otras.
Uno de los objetivos de la ciencia es saber cómo se comportan las variables de un sistema para poder hacer predicciones sobre su futuro comportamiento. De acuerdo a su naturaleza, cada variable requiere un tratamiento específico para obtener de ella la máxima información.
La cantidad de variables a estudiar es enorme, pero examinando con atención el grupo antes mencionado, notamos de inmediato que algunas pueden ser expresadas en forma numérica, mientras que otras no.
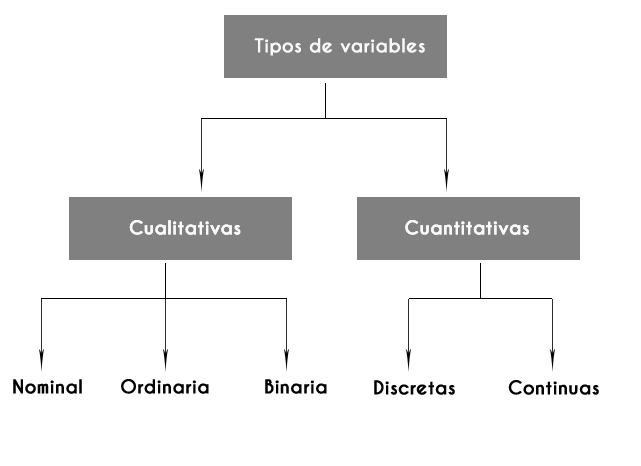
Esto nos da pie para una clasificación inicial de las variables estadísticas en dos tipos fundamentales: cualitativas y numéricas.
Tipos de variables estadísticas
– Variables cualitativas
Como su nombre lo indica, las variables cualitativas se utilizan para designar categorías o cualidades.
Un conocido ejemplo de este tipo de variables es el estado civil: soltero, casado, divorciado o viudo. Ninguna de estas categorías es mayor que la otra, solamente designa una situación diferente.
Más variables de este tipo son:
-Nivel académico
-Mes de año
-Marca de auto que se conduce
-Profesión
-Nacionalidad
-Países, ciudades, distritos, condados y otras divisiones territoriales.
Una categoría también puede designarse mediante un número, por ejemplo el número de teléfono, el número de casa, de calle o el código postal, sin que esto represente una valoración numérica, sino más bien una etiqueta.

Variables nominales, ordinales y binarias
Las variables cualitativas pueden ser a su vez:
–Nominales, que asignan un nombre a la cualidad, como puede ser el color por ejemplo.
–Ordinales, que representan orden, como el caso de una escala de estratos socioeconómicos (alto, medio, bajo) o de opiniones acerca de alguna clase de propuesta (a favor, indiferente, en contra). *
–Binarias, también llamadas dicotómica, solamente hay dos valores posibles, como el sexo. A esta variable se le puede asignar una etiqueta numérica, como 1 y 2, sin que represente valoración numérica o alguna clase de orden.
*Algunos autores incluyen a las variables ordinales en el grupo de las variables cuantitativas, que se describen seguidamente. Se debe a que expresan orden o jerarquía.
– Variables numéricas o cuantitativas
A estas variables sí se les asigna un número, ya que representan cantidades, como por ejemplo el salario, la edad, las distancias y las calificaciones obtenidas en un examen.
Son ampliamente utilizadas para contrastar preferencias y estimar tendencias. Se pueden asociar con las variables cualitativas y construir gráficos de barras e histogramas que facilitan el análisis visual.
Algunas variables numéricas pueden ser transformadas en variables cualitativas, pero lo contrario no es posible. Por ejemplo la variable numérica “edad”, puede dividirse en intervalos con etiquetas asignadas, como bebés, niños, adolescentes, adultos y ancianos.
Sin embargo, se debe destacar que hay operaciones que se pueden hacer con las variables numéricas, que evidentemente no se pueden llevar a cabo con las cualitativas, por ejemplo calcular promedios y otros estimadores estadísticos.
Si lo que se quiere es hacer cálculos, hay que mantener la variable “edad” como variable numérica. Pero otras aplicaciones puede que no requiera detalle numérico, para estas bastaría con dejar las etiquetas nombradas.
Las variables numéricas se dividen a su vez en dos grandes categorías: variables discretas y variables continuas.
Variables discretas
Las variables discretas únicamente toman ciertos valores y se caracterizan por ser contables, por ejemplo el número de hijos de una familia, la cantidad de mascotas, el número de clientes que visitan a diario una tienda y los suscriptores de una compañía de cable, por mencionar algunos ejemplos.
Definiendo por ejemplo la variable “número de mascotas”, esta toma sus valores del conjunto de los números naturales. Una persona puede tener 0, 1, 2, 3 o más mascotas, pero nunca 2.5 mascotas, por ejemplo.
Sin embargo, una variable discreta necesariamente tiene valores naturales o enteros. Los números decimales también sirven, ya que el criterio para determinar si una variable es discreta es que esta sea contable o numerable.
Por ejemplo supongamos que se define como variable la fracción de bombillos defectuosos en una fábrica, tomados de una muestra de 50, 100 o N bombillos al azar.
Si ningún bombillo es defectuoso, la variable toma el valor 0. Pero si 1 de N bombillos está defectuoso, la variable vale 1 /N, si hay dos defectuosos es 2/N y así sucesivamente hasta llegar al evento de que los N bombillos estaban defectuosos y en tal caso la fracción sería 1.
Variables continuas
A diferencia de las variables discretas, las variables continuas pueden tomar cualquier valor. Por ejemplo, el peso de los estudiantes que cursan determinada asignatura, la estatura, la temperatura, el tiempo, la longitud y muchas otras más.
Como la variable continua toma infinitos valores, se pueden hacer con ella cálculos de todo tipo con la precisión deseada, con solo ajustar el número de decimales.
En la práctica hay variables continuas que pueden expresarse como variables discretas, por ejemplo la edad de una persona.
La edad exacta de una persona puede contarse en años, meses, semanas, días y más, dependiendo de la precisión que se desee, pero usualmente se redondea en años y de esta manera pasa a ser discreta.
Los ingresos de una persona también son una variable continua, pero suele trabajarse mejor si se establecen intervalos.
– Variables dependientes e independientes
Las variables dependientes son las que se miden durante un experimento, para estudiar la relación que tienen con otras, que serían consideradas las variables independientes.
Ejemplo 1
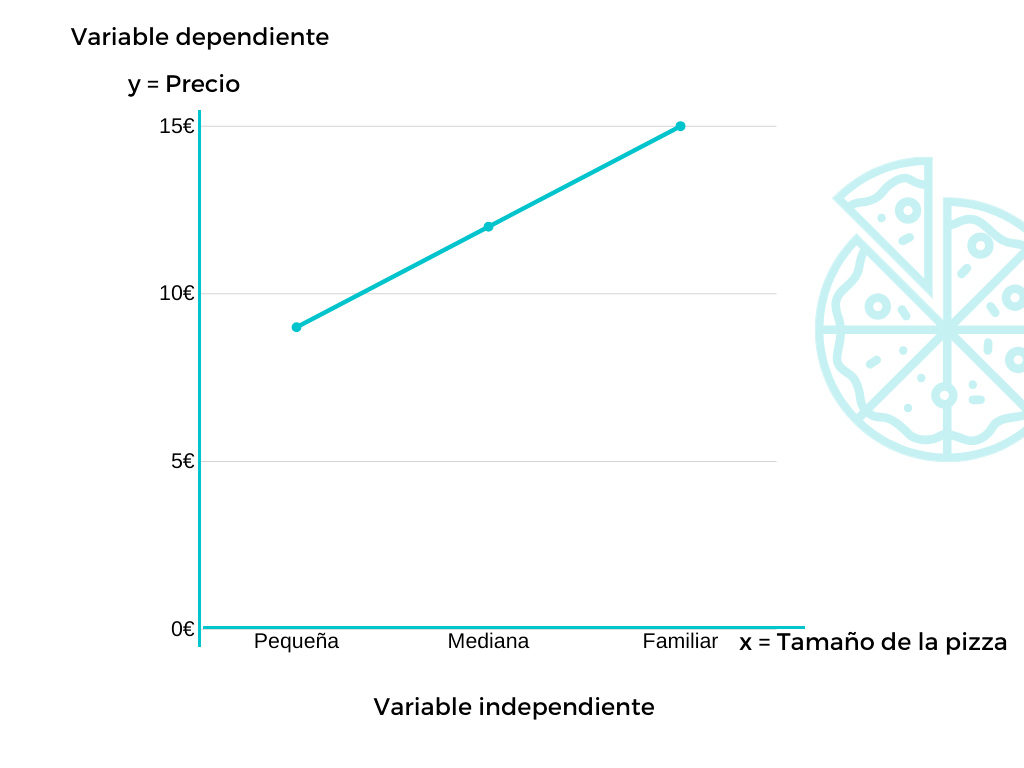
En este ejemplo vamos a ver la evolución de precios que sufren las pizzas de un local de comida en función a su tamaño.
La variable dependiente (y) sería el precio, mientras la variable independiente (x) sería el tamaño. En este caso, la pizza pequeña vale 9€, la mediana 12€ y la familiar 15€.
Es decir, a medida que aumenta el tamaño de la pizza, esta cuesta más. Por lo tanto, el precio sería dependiente del tamaño.
Esta función sería y = f(x)
Ejemplo 2
Un ejemplo simple: se quiere examinar el efecto que producen los cambios de la corriente I a través de un alambre de metal, para lo cual se mide el voltaje V entre los extremos de este.
La variable independiente (la causa) es la corriente, mientras que la variable dependiente (el efecto) es el voltaje, cuyo valor depende de la corriente que transita por el alambre.
En el experimento lo que se busca es saber cómo es la ley para V cuando I se hace variar. Si la dependencia del voltaje con la corriente resulta ser lineal, esto es: V ∝ I, el conductor es óhmico y la constante de proporcionalidad es la resistencia del alambre.
Pero el hecho de que una variable sea independiente en un experimento, no significa que lo sea en otro. Eso dependerá del fenómeno bajo estudio y del tipo de investigación que se quiera realizar.
Por ejemplo, la corriente I que transita un conductor cerrado girando en un campo magnético constante, pasa a ser la variable dependiente con respecto al tiempo t, el cual pasaría a ser la variable independiente.
Referencias
- Berenson, M. 1985. Estadística para administración y economía. Interamericana S.A.
- Canavos, G. 1988. Probabilidad y Estadística: Aplicaciones y métodos. McGraw Hill.
- Devore, J. 2012. Probability and Statistics for Engineering and Science. 8th. Edition. Cengage.
- Enciclopedia Económica. Variables continuas. Recuperado de: enciclopediaeconomica.com.
- Levin, R. 1988. Estadística para Administradores. 2da. Edición. Prentice Hall.
- Walpole, R. 2007. Probabilidad y Estadística para Ingeniería y Ciencias. Pearson.
