Función logarítmica: propiedades, ejemplos, ejercicios

La función logarítmica es una relación matemática que asocia a cada número real positivo x con su logaritmo y en una base a. Esta relación cumple con los requisitos para ser una función: cada elemento x perteneciente al dominio tiene una imagen única.

Por lo tanto:

f(x) = y = log_a x , con a > 0 y distinto de 1.

Las principales propiedades de la función logarítmica son:

-Su dominio son todos los reales mayores que 0, sin incluir al 0. En otras palabras, no existe el logaritmo de 0 ni de números negativos en ninguna base. En forma de intervalo:

Dom _f = (0, ∞+)

-El logaritmo de un número sí puede ser negativo, positivo o 0, de manera que su rango o recorrido es:

Rgo _f = (-∞, ∞+)

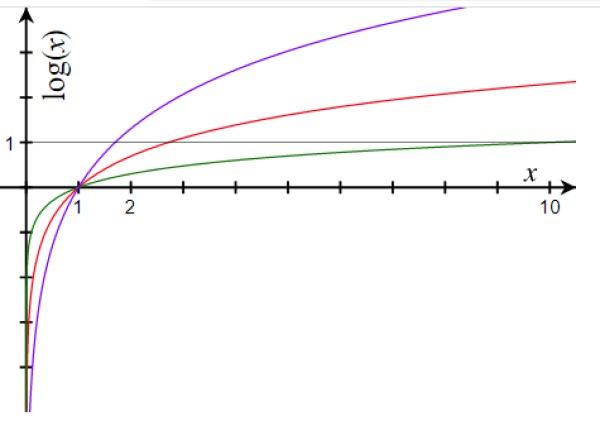
-La función logarítmica es siempre creciente para a >1 y decreciente para a1.

-El inverso de f(x) = log_a x es la función exponencial.

En efecto, la función logaritmo en base a, es la función inversa de la función potencial:

f^-1(x) = a^y

Ya que el logaritmo en base a de un número x, es el número y al cual debe elevarse la base a para obtener x.

-El logaritmo de la base siempre es 1. Así, la gráfica de f(x) = log_a x siempre intersecta al eje x en el punto (1,0)

-La función logarítmica es trascendente y no puede ser expresada como polinomio o como cociente de estos. Además del logaritmo, este grupo incluye a las funciones trigonométricas y a la exponencial, entre otras.

Índice del artículo

• 1 Ejemplos
• 2 Las ventajas de los logaritmos
  • 2.1 Ejemplo
• 3 Ejercicio de aplicación: la escala de Richter
  • 3.1 Solución
• 4 Referencias

Ejemplos

La función logarítmica se puede establecer mediante diversas bases, pero las más utilizadas son 10 y e, donde e es el número de Euler igual a 2,71828….

Cuando se utiliza la base 10 el logaritmo se llama logaritmo decimal, logaritmo vulgar, de Briggs o simplemente logaritmo a secas.

Y si se usa el número e, entonces se llama logaritmo neperiano, por John Napier, el matemático escocés que descubrió los logaritmos.

La notación empleada para cada uno es la siguiente:

-Logaritmo decimal: log₁₀ x = log x

-Logaritmo neperiano: ln x

Cuando se va a emplear otra base, es absolutamente necesario indicarla como subíndice, porque el logaritmo de cada número es distinto según la base que se vaya a emplear. Por ejemplo, si se trata de logaritmos en base 2 se escribe:

y = log₂ x

Veamos el logaritmo del número 10 en tres distintas bases, para ilustrar este punto:

log 10 = 1

ln 10 = 2.30259

log₂ 10 = 3.32193

Las calculadoras comunes solamente traen logaritmos decimal (función log) y logaritmo neperiano (función ln). En Internet hay calculadoras con otras bases. En todo caso, el lector puede verificar, con ayuda de la misma, que con los valores anteriores se cumple:

10¹ = 10

e^2.3026 = 10.0001

2^3.32193 = 10.0000

Las pequeñas diferencias de decimales se deben a la cantidad de decimales tomadas en el cálculo del logaritmo.

Las ventajas de los logaritmos

Entre las ventajas de usar los logaritmos está la facilidad que brindan para trabajar con números grandes, usando su logaritmo en vez del número directamente.

Esto es posible porque la función logaritmo crece más despacio a medida que los números son mayores, tal como apreciamos en la gráfica.

Así que aún tratándose de números muy grandes, sus logaritmos son muchísimo más pequeños, y manipular números pequeños siempre es más fácil.

Además los logaritmos cumplen las siguientes propiedades:

–Producto: log (a.b) = log a + log b

–Cociente: log (a/b) = log a – log b

–Potencia: log a^b = b.log a

Y de esta forma, los productos y cocientes pasan a ser sumas y restas de números más pequeños, mientras que la potenciación se transforma en producto sencillo aunque la potencia sea elevada.

Por eso los logaritmos permiten expresar números que varíen en rangos muy grandes de valores, tales como la intensidad del sonido, el pH de una solución, el brillo de las estrellas, la resistencia eléctrica y la intensidad de los terremotos en la escala de Richter.

Veamos un ejemplo del manejo de las propiedades de los logaritmos:

Ejemplo

Hallar el valor de x en la siguiente expresión:

log (5x +1) = 1 + log (2x-1)

Respuesta

Tenemos aquí una ecuación logarítmica, en vista de que la incógnita está en el argumento del logaritmo. Se resuelve dejando un solo logaritmo a cada lado de la igualdad.

Comenzamos colocando todos los términos que contienen “x” a la izquierda de la igualdad, y los que contienen solo números a la derecha:

log (5x+1) – log (2x-1) = 1

A la izquierda tenemos la resta de dos logaritmos, que se puede escribir como el logaritmo de un cociente:

log [(5x+1)/ (2x-1)] = 1

Sin embargo, a la derecha está el número 1, el cual podemos expresar como log 10, tal como vimos anteriormente. Entonces:

log [(5x+1)/ (2x-1)] = log 10

Para que la igualdad se cumpla, los argumentos de los logaritmos deben ser iguales:

(5x+1)/ (2x-1) = 10

5x + 1 = 10 (2x – 1)

5x + 1 = 20 x – 10

-15 x = -11

x = 11/15

Ejercicio de aplicación: la escala de Richter

En 1957 ocurrió un terremoto en México cuya magnitud fue de 7.7 en la escala Richter. En 1960 ocurrió otro terremoto de mayor magnitud en Chile, de 9.5.

Calcular cuántas veces fue el terremoto de Chile más intenso que el de México, sabiendo que la magnitud M_R en la escala de Richter viene dada por la fórmula:

M_R = log (10⁴ I)

Solución

La magnitud en la escala de Richter de un terremoto es una función logarítmica. Vamos a calcular la intensidad de cada terremoto, puesto que tenemos las magnitudes Richter. Hagámoslo paso a paso:

–México: 7.7 = log (10⁴ I)

Como la inversa de la función logaritmo es la exponencial, aplicamos esta a ambos lados de la igualdad con la intención de despejar I, que se encuentra en el argumento del logaritmo.

Dado que son logaritmos decimales, la base es 10. Entonces:

10 ^7.7 = 10⁴ I

La intensidad del terremoto de México fue:

I_M = 10 ^7.7 / 10⁴ = 10^3.7

 –Chile: 9.5 = log (10⁴ I)

El mismo procedimiento nos lleva a la intensidad del terremoto chileno I_Ch:

I_Ch = 10 ^9.5 / 10⁴ = 10^5.5

 Ahora podemos comparar ambas intensidades:

I_Ch / I_M = 10^5.5 / 10^3.7 = 10^1.8 = 63.1

 I_Ch = 63.1. I_M

El terremoto de Chile fue unas 63 veces más intenso que el de México. Como la magnitud es logarítmica, crece más despacio que la intensidad, así que una diferencia de 1 en la magnitud, significa una amplitud 10 veces mayor de la onda sísmica.

La diferencia entre las magnitudes de ambos terremotos es de 1.8, por lo tanto podíamos esperar una diferencia en intensidades más cercana a 100 que a 10, como efectivamente sucedió.

De hecho si la diferencia hubiese sido de 2 exactamente, el terremoto chileno habría sido 100 veces más intenso que el mexicano.

Referencias

1. Carena, M. 2019. Manual de Matemática Preuniversitaria. Universidad Nacional del Litoral.
2. Figuera, J. 2000. Matemática 1er. Año Diversificado. ediciones CO-BO.
3. Jiménez, R. 2008. Álgebra. Prentice Hall.
4. Larson, R. 2010. Cálculo de una variable. 9na. Edición. McGraw Hill.
5. Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.