Ecuación de Clausius-Clapeyron: para qué sirve, ejemplos, ejercicios

La ecuación de Clausius-Clapeyron es aquella que relaciona los cambios en la presión de vapor y la temperatura, en una transición de fase o cambio de estado. Aplica para sublimaciones, evaporaciones, fusiones, o en incluso en cambios de fases cristalinas. Cabe mencionar que dicha ecuación aplica para una sustancia pura que se encuentra en equilibrio.

Esta ecuación deriva de las leyes termodinámicas y de los diagramas P-T para una sustancia, en donde se observa la línea de coexistencia; aquella que separa dos fases distintas (líquido-vapor, sólido-líquido, etc.). Para traspasar dicha línea, es necesaria la ganancia o pérdida de calor, tal como la entalpía de vaporización, ΔH_vap.

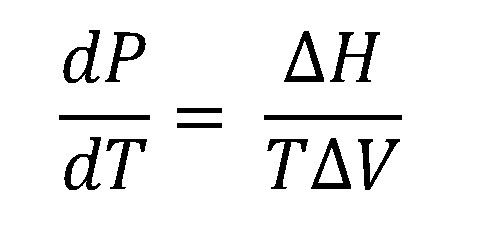
En la imagen superior se muestra la ecuación de Clausius-Clapeyron antes de ser integrada. Normalmente suele aplicarse para sistemas líquido-vapor, donde se usa ΔH_vap y se desea calcular cuál será la presión de vapor del líquido a cierta temperatura. Asimismo, sirve para calcular el ΔH_vap de un determinado líquido en un rango de temperaturas.

La ecuación de Clausisu-Clapeyron también se utiliza con bastante frecuencia para estudiar los cambios de presión en los sólidos volátiles; es decir, se considera la entalpía de sublimación, ΔH_sub.

Índice del artículo

• 1 ¿Para qué sirve la ecuación de Clausisu-Clapeyron?
  • 1.1 Cálculo de cambios de presiones y entalpías de vaporización
  • 1.2 Determinación de cambios de fase
• 2 Ejemplos de uso
• 3 Ejercicios resueltos
  • 3.1 – Ejercicio 1
  • 3.2 – Ejercicio 2
• 4 Referencias

¿Para qué sirve la ecuación de Clausisu-Clapeyron?

Cálculo de cambios de presiones y entalpías de vaporización

A partir de la ecuación de Clausius-Clapeyron de arriba, se procede a tener algunas consideraciones matemáticas para finalmente realizar una integración. Por ejemplo, para un sistema líquido-vapor, se asume que ΔH_vap no varía con la temperatura, y que ΔV corresponde exclusivamente al volumen del vapor, despreciando el volumen del líquido (V_vapor-V_líquido = V_vapor).

Asumiendo que el vapor se comporta como un gas ideal e integrando, se obtiene la ecuación de Clausius-Clapeyron integrada:

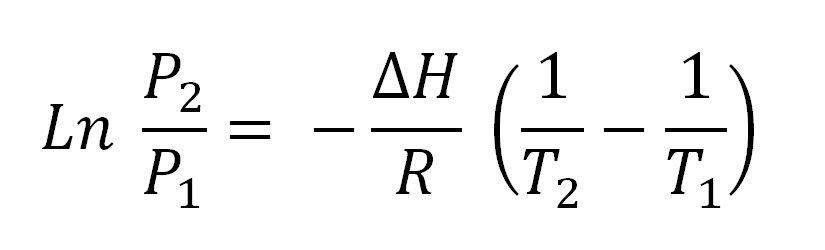
Esta ecuación corresponde al de una recta que se grafica como:

Ln P vs 1/T

Y cuya pendiente negativa es (ΔH/R). Para que se cumpla esta ecuación, por lo tanto, ΔH debe ser constante en el intervalo de temperatura (T₂-T₁) en que se miden las presiones de vapor en equilibrio con el líquido.

De esta manera, si se asume que ΔH varía poco dentro de pequeños intervalos de temperatura, es posible utilizar la ecuación de esta recta para predecir los cambios en la presión de vapor de un líquido; y aún más, se puede determinar su ΔH de vaporización.

Mientras más grandes sean los intervalos de temperaturas considerados, más grande será la desviación de esta ecuación de los datos experimentales, y menos se cumplirá.

Determinación de cambios de fase

Así, la ecuación de Clausius-Clapeyron viene a ser el desarrollo de una recta tangente a la línea de coexistencia entre dos fases físicas, la cual se observa en cualquier diagrama P-T para una sustancia.

Si ocurre un cambio de fase, habrá un cambio en la pendiente, y ΔH no será el mismo. Por lo tanto, cuando se evidencian fuertes desviaciones y la ecuación falla por mucho, es señal de que en el intervalo de temperatura la sustancia está experimentando otro cambio de fase. Es decir, deja de ser un sistema líquido-vapor, ya que se pasa a la línea de coexistencia correspondiente a los equilibrios sólido-líquido o sólido-vapor.

Ejemplos de uso

– La ecuación de Clausius-Clapeyron se ha usado en meteorología para estudiar el comportamiento de las nubes, incluso de aquellas presentes en otros planetas o lunas con atmósferas.

– Se ha usado en la determinación de la entalpía de fusión de varios metales como el sodio y el galio, y para extrapolar sus presiones de vapores a muy altas temperaturas.

– También se ha usado para determinar la entalpía de vaporización de sustancias tales como el cloro gaseoso, el tetracloruro de carbono, el agua líquida, el hielo y el yodo.

– Asimismo, ha servido para estudiar los cambios de fase en estructuras cristalinas. En este último ejemplo, la ecuación integrada de Clausius-Clapeyron luce notablemente distinta, pues no pueden hacerse para ΔV las mismas consideraciones que se toman para el sistema líquido-vapor. Las variaciones de volumen de una fase a la otra esta vez son pequeñas.

Ejercicios resueltos

– Ejercicio 1

La presión de vapor del hielo es 4.58 torr a 0 °C y 1.95 torr a -10 °C. ¿Cuál es su entalpía de sublimación en ese rango de temperaturas?

Nótese que tenemos dos presiones y dos temperaturas:

P₁ = 4.58 torr

P₂ = 1.95 torr

T₁ = 0 °C + 273 = 273 K

T₂ = -10 °C + 273 = 263 K

Convertimos las unidades de temperatura de °C a K, pues la constante R de los gases posee K en sus unidades:

R = 8.314 J/K

Así, utilizamos la ecuación integrada de Clausius-Clapeyron y despejamos ΔH_sub, lo cual quedaría como:

ΔH_sub = -RLn (P₂/P₁) / (1/T₂ – 1 /T₁)

Para mayor comodidad se procederá a sustituir solamente con los números, pero sabiendo que la unidad final será el Joule:

ΔH_sub = -(8.314) Ln (1.95/4.58) / (1/263 – 1/273)

= 50.97 J

O 51.07 J considerando pocos decimales. Este valor presentará oscilaciones dependiendo de los intervalos T₂-T₁ y de las presiones de vapor determinadas.

– Ejercicio 2

El punto de ebullición del etanol a una presión de 760 torr (1 atm) es de 78.3 °C, y su entalpía de vaporización es de 39.3 kJ. ¿Cuál será su presión de vapor a una temperatura de 46 °C?

Identificamos los datos:

P₁ = 760 torr

P₂ = ?

T₁ = 78.3 °C + 273 = 351.3 K

T₂ = 46 °C + 273 = 319 K

ΔH_vap = 39.3 kJ o 39300 J

Así pues, debemos despejar P₂ de la ecuación integrada de Clausius-Clapeyron. Nuevamente, se omitirán las unidades para mayor comodidad y los cálculos se irán desarrollando paso a paso:

Ln (P₂/P₁) = -(ΔH_vap/R) (1/T₂ – 1/T₁)

Ln (P₂/760) = -(39300/8.314) (1/319 – 1/351.3)

Ln (P₂/760) = -1.36

Aplicando la función exponencial a ambos lados de la ecuación para poder despejar P₂ tendremos:

e (ln P₂/760) = e^(-1.36)

P₂/760 = 0.256

P₂ = 0.256 (760)

= 195 torr

A menor temperatura (46 °C), menor presión de vapor (195 torr). De hecho, al tener el etanol una presión de 760 torr a 78.3 °C, estamos hablando de su punto de ebullición normal. Este es el comportamiento que se espera para todos los líquidos

En general, los ejercicios de Clausius-Clapeyron de este tipo consisten en despejar P₂, T₂ o ΔH de vaporización o sublimación. Los cálculos cambian notablemente cuando se debe considerar también ΔV, sobre todo cuando se trata de sistemas o equilibrios sólido-líquido.

Referencias

1. Whitten, Davis, Peck & Stanley. (2008). Química. (8va ed.). CENGAGE Learning.
2. Wikipedia. (2020). Clausius-Clapeyron relation. Recuperado de: en.wikipedia.org
3. San José State University. (s.f.). The Clausius-Clapeyron Equation:
   Its Derivation and Application in Meteorology. Recuperado de: sjsu.edu
4. Bodner Group. (s.f.). The Clausius-Clapeyron Equation. Recuperado de: chemed.chem.purdue.edu
5. Chieh C. & Censullo A. (18 de mayo de 2020). Clausius-Clapeyron Equation. Chemistry LibreTexts. Recuperado de: chem.libretexts.org
6. Walter J. Moore. (1962). Physical Chemistry. (Fourth edition). Longmans.