Plano cartesiano: qué es, características, elementos, ejemplos
¿Qué es el plano cartesiano?
El plano cartesiano consiste en un par de rectas perpendiculares entre sí y que se intersectan en un punto. Una de las rectas es vertical y la otra horizontal, tomando al punto de intersección como el origen del sistema.
El objetivo es ubicar fácilmente cualquier punto plano mediante un par de valores: las coordenadas. Para ello, sobre cada una de las rectas se construye una escala con números enteros, los positivos se escriben en una dirección y los negativos en la otra, como se muestra en la siguiente figura:
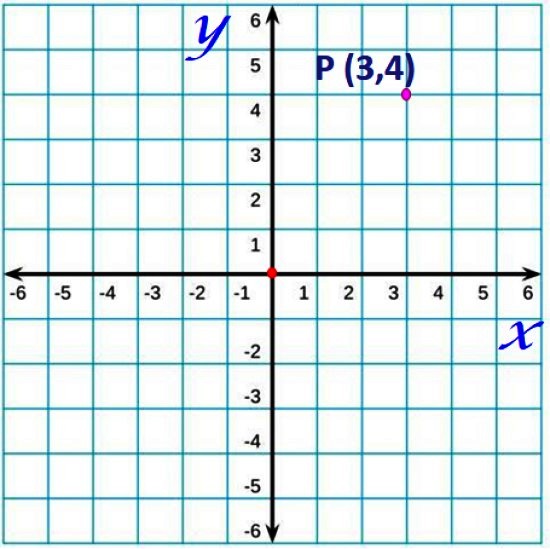
Por convención, al eje horizontal se suele llamar eje x y al vertical como eje y.
Un punto cualquiera del plano tendrá coordenadas especificadas por un par ordenado (x,y). Por ejemplo, el punto P de coordenadas (3,4), localizado a 3 unidades a la derecha del origen y 4 unidades hacia arriba, en la figura superior. Es similar a un mapa, que indica la latitud y la longitud de una ubicación determinada.
Como son necesarias dos coordenadas, se dice que el plano es bidimensional, pero el concepto se extiende fácilmente a tres dimensiones, añadiendo un eje coordenado más, que por lo general se denota como eje z. En tal caso las coordenadas toman la forma (x,y,z).
El plano cartesiano recibe su nombre del científico francés René Descartes (1596-1650), quien lo formalizó en su obra Discurso del Método de 1637, aunque existen antecedentes en las obras de Apolonio de Perga (262-190 aC), el matemático que descubrió las curvas cónicas: circunferencia, elipse, parábola e hipérbola.
Características del plano cartesiano
– Tanto el eje x como el eje y se extienden infinitamente por ambos extremos, y se intersectan entre sí perpendicularmente (en un ángulo de 90 grados). Esta característica se llama ortogonalidad.
– El punto donde ambos ejes se intersectan se conoce como origen o punto cero.
– El sistema de coordenadas divide al plano en cuatro regiones llamadas cuadrantes.
– Las ubicaciones en el plano de coordenadas se describen como pares ordenados.
– Cada punto sobre el plano cartesiano está asociado a una coordenada x única y a una coordenada y única.
Elementos del plano cartesiano
Los elementos del plano cartesiano son los siguientes:
-Las rectas numéricas o ejes coordenados x e y, si se trata del plano. El eje y recibe el nombre de eje de las ordenadas, mientras que el eje x es el eje de las abscisas. Cuando se trata del espacio, entonces se añade el eje z, capaz de representar tanto la altura como la profundidad.
-El origen, que es el punto de intersección de los ejes.
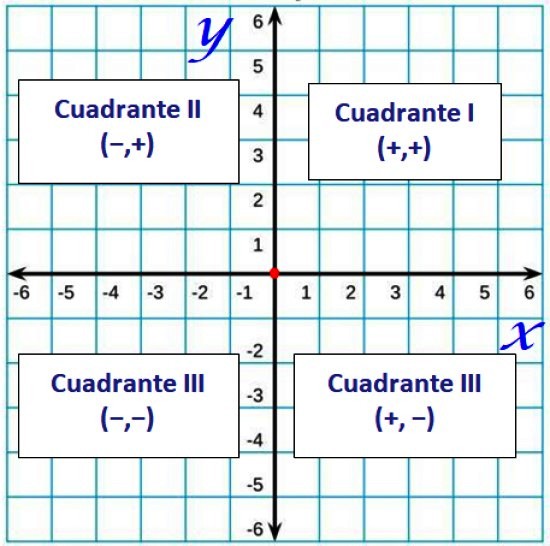
-Los cuadrantes, que son las regiones que los ejes coordenados determinan sobre el plano y se cuentan en el sentido contrario a las manecillas del reloj, comenzando por el primer cuadrante. Se definen del siguiente modo:
- Primer cuadrante: ejes x e y positivos.
- Segundo cuadrante: correspondiente al eje x negativo y al eje y positivo.
- Tercer cuadrante: tiene ambos ejes negativos.
- Cuarto cuadrante: con el eje x positivo y el eje y negativo.
Generalmente, los cuadrantes se denotan en números romanos, así:
Pares ordenados y distancia entre dos puntos
Los pares ordenados son las coordenadas de cada punto, en las cuales siempre se coloca la coordenada x en primer lugar, como en el ejemplo de la figura 1. Las coordenadas (3,4) del punto P indican que x = 3 y y = 4.
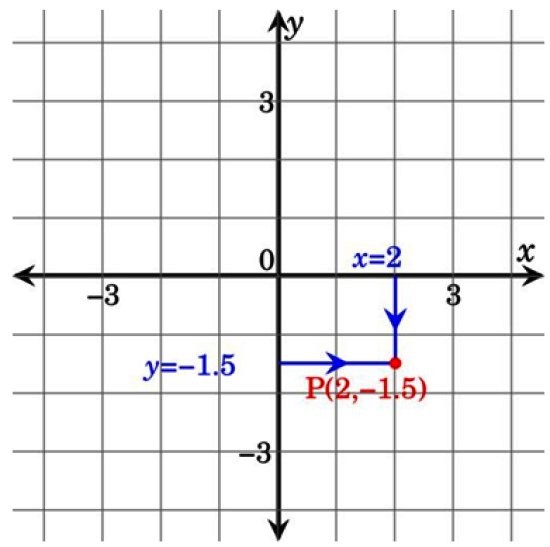
En esta otra figura a continuación, el punto P pertenece al IV cuadrante y tiene coordenadas (2; −1.5). Obsérvese que al proyectar líneas desde los ejes coordenados hasta el punto P se forma un rectángulo. Esta es la razón por la cual a las coordenadas cartesianas también se las llama coordenadas rectangulares.
Aplicaciones del plano cartesiano
El plano cartesiano tiene multitud de aplicaciones en muchos campos. Inicialmente, Descartes lo introdujo para graficar ecuaciones de curvas en el plano, motivo por el cual se le considera como el padre de la geometría analítica.
Sin embargo, su uso se extiende para graficar todo tipo de relaciones y funciones, como por ejemplo:
-Seguir la trayectoria de un cuerpo con movimiento parabólico, circular o curvilíneo en general.
-Determinar gráficamente la manera en la que se relacionan dos variables a través de una función.
-Ubicar puntos sobre terrenos planos para facilitar las mediciones sobre ellos.
Referencias
- Math is Fun. Cartesian coordinates. Recuperado de: mathsisfun.com/data/cartesian-coordinates.
- The Cartesian Plane. Recuperado de: dl.uncw.edu.
