Error de muestreo: fórmulas y ecuaciones, cálculo, ejemplos
El error de muestreo o error muestral en estadística, es la diferencia que hay entre el valor medio de una muestra respecto al valor medio de la población total. Para ilustrar la idea, imaginemos que la población total de una ciudad es de un millón de personas, de la que se quiere su talla media de zapatos, para lo cual se toma una muestra al azar de mil personas.
La talla promedio que surge de la muestra no necesariamente coincidirá con la de la población total, aunque si la muestra no es sesgada el valor ha de ser cercano. Esa diferencia entre el valor medio de la muestra y el de la población total es el error muestral.
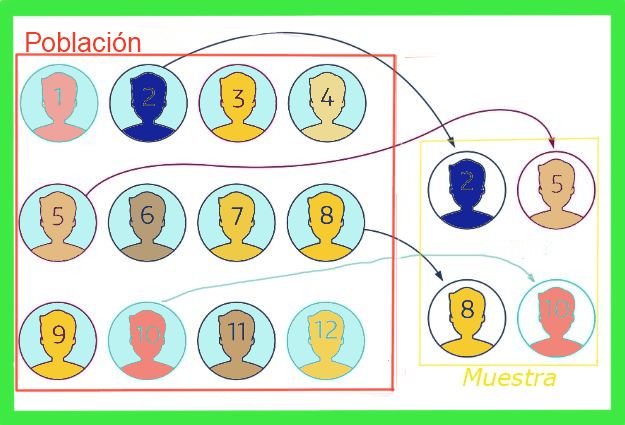
Por lo general se desconoce el valor medio de la población total, pero existen técnicas para disminuir dicho error y fórmulas para estimar el margen de error muestral que se expondrán en este artículo.
Índice del artículo
Pongamos por caso, que se quiere conocer el valor medio de determinada característica medible x en una población de tamaño N, pero como N es un número grande no es viable hacer el estudio sobre la población total, entonces se procede a tomar una muestra aleatoria de tamaño n
El valor medio de la muestra lo denotamos por
Supongamos que se toman m muestras de la población total N, todas de igual tamaño n con valores medios
Estos valores medios no serán idénticos entre sí y estarán todos alrededor del valor medio poblacional μ. El margen de error muestral E indica la separación esperada de los valores medios
El margen de error estándar ε de la muestra de tamaño n es:
ε = σ/√n
donde σ es la desviación estándar (la raíz cuadrada de la varianza), la cual se calcula mediante la siguiente fórmula:
σ = √[(x –
El significado del margen de error estándar ε es el siguiente:
El valor medio
En la sección previa se dio la fórmula para hallar el margen de error estándar de una muestra de tamaño n, donde la palabra estándar indica que se trata de un margen de error con 68% de confianza.
Esto indica que si se tomasen muchas muestras del mismo tamaño n, el 68% de ellas darán valores medios
Hay una regla sencilla, llamada la regla 68-95-99.7 que nos permite hallar el margen de error muestral E para niveles de confianza del 68%, 95% y 99,7% fácilmente, ya que este margen es 1⋅ε, 2⋅ε y 3⋅ε respectivamente.
Si el nivel de confianza γ no es alguno de los anteriores, entonces el error de muestreo es la desviación estándar σ multiplicada por el factor Zγ, el cual se obtiene mediante el siguiente procedimiento:
1.- Primero se determina el nivel de significancia α el cual se calcula a partir del nivel de confianza γ mediante la siguiente relación: α = 1 – γ
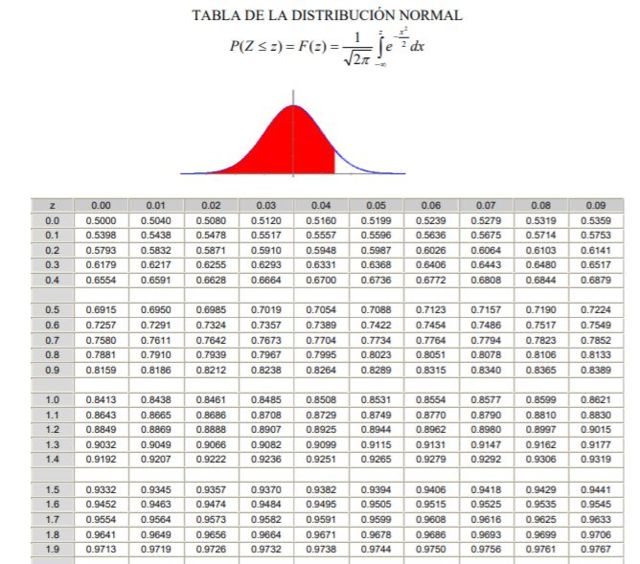
2.- Luego hay que calcular el valor 1 – α/2 = (1 + γ)/2, que corresponde a la frecuencia normal acumulada entre -∞ y Zγ, en una distribución normal o gaussiana tipificada F(z), cuya definición puede verse en la figura 2.
3.- Se resuelve la ecuación F(Zγ) = 1 – α/2 por medio de las tablas de la distribución normal (acumulada) F, o mediante una aplicación informática que disponga de la función gaussiana tipificada inversa F-1.
En este último caso se tiene:
Zγ = G-1(1 – α/2).
4.- Por último, se aplica esta fórmula para el error de muestreo con un nivel de confiabilidad γ:
E = Zγ⋅(σ/√n)
Calcular el margen de error estándar en el peso promedio de una muestra de 100 recién nacidos. El cálculo del peso promedio fue
Solución
El margen de error estándar es ε = σ/√n = (1,500 kg)/√100 = 0,15 kg. Lo que significa que con estos datos se puede inferir que el peso del 68% de los recién nacidos está comprendido entre 2,950 kg y 3.25 kg.
Determine el margen de error muestral E y el rango de peso de 100 recién nacidos con un nivel de confianza del 95% si el peso promedio es de 3,100 kg con desviación estándar σ = 1,500 kg.
Solución
Si se aplica la regla 68; 95; 99.7→ 1⋅ε; 2⋅ε; 3⋅ε, se tiene:
E = 2⋅ε = 2⋅0,15 kg = 0,30 kg
Es decir que el 95% de los recién nacidos tendrán pesos comprendidos entre 2,800 kg y 3,400 kg.
Determine el rango de pesos de los recién nacidos del ejemplo 1 con un margen de confianza de 99,7%.
Solución
El error muestral con un 99,7% de confianza es 3 σ/√n, que para nuestro ejemplo es E = 3 *0,15 kg = 0,45 kg. De acá se infiere que el 99,7% de los recién nacidos tendrán pesos comprendidos entre 2,650 kg y 3,550 kg.
Determinar el factor Zγ para un nivel de confiabilidad del 75%. Determine el margen de error de muestreo con este nivel de confiabilidad para el caso planteado en el ejemplo 1.
Solución
El nivel de confianza es γ= 75% = 0,75 que se relaciona con el nivel de significaciónα mediante la relación γ= (1 – α), de modo que el nivel de significación es α = 1 – 0,75 = 0,25.
Esto significa que la probabilidad normal acumulada entre -∞ y Zγ es:
P( Z ≤ Zγ ) = 1 – 0,125 = 0,875
Lo que se corresponde con un valor Zγ de 1,1503, tal como se muestra en la figura 3.
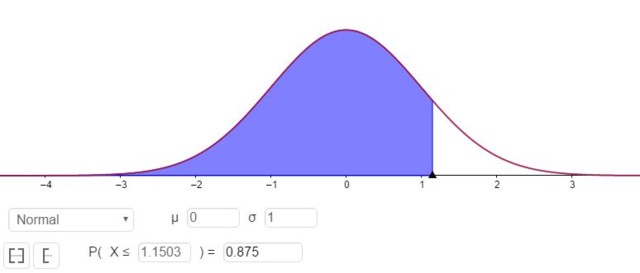
Es decir que el error de muestreo es E = Zγ⋅(σ/√n)= 1,15⋅(σ/√n).
Cuando se aplica a los datos del ejemplo 1, da un error de:
E= 1,15*0,15 kg = 0,17 kg
Con un nivel de confianza de 75%.
¿Cuál es el nivel de confianza si Zα/2 = 2.4 ?
Solución
P( Z ≤ Zα/2 ) = 1 – α/2
P( Z ≤ 2.4 ) = 1 – α/2 = 0,9918 → α/2 = 1 – 0,9918 = 0,0082 → α = 0,0164
El nivel de significancia es:
α = 0,0164 = 1,64%
Y por último, el nivel de confianza queda:
1- α = 1 – 0,0164 = 100% – 1,64% = 98,36 %
- Canavos, G. 1988. Probabilidad y Estadística: Aplicaciones y métodos. McGraw Hill.
- Devore, J. 2012. Probability and Statistics for Engineering and Science. 8th. Edition. Cengage.
- Levin, R. 1988. Estadística para Administradores. 2da. Edición. Prentice Hall.
- Sudman, S.1982. Asking Questions: A Practical Guide to Questionnaire Design. San Francisco. Jossey Bass.
- Walpole, R. 2007. Probabilidad y Estadística para Ingeniería y Ciencias. Pearson.
- Wonnacott, T.H. and R.J. Wonnacott. 1990. Introductory Statistics. 5th Ed. Wiley
- Wikipedia. Sampling error. Recuperado de: en.wikipedia.com
- Wikipedia. Margin of error. Recuperado de: en.wikipedia.com
