Teorema de superposición: explicación, aplicaciones, ejercicios resueltos
El teorema de superposición, en circuitos eléctricos, establece que el voltaje entre dos puntos, o la corriente a través de ellos, es la suma algebraica de los voltajes (o de las corrientes si es el caso), debidos a cada fuente, como si cada una actuara de manera independiente.
Este teorema permite analizar circuitos lineales que contengan más de una fuente independiente, ya que solamente se requiere calcular la contribución de cada una por separado.

La dependencia lineal es determinante para que el teorema se aplique. Un circuito lineal es aquel cuya respuesta es directamente proporcional a la entrada.
Por ejemplo, la ley de Ohm aplicada a una resistencia eléctrica establece que V = i.R, donde V es el voltaje, R es la resistencia e i es la corriente. Se trata entonces de una dependencia lineal del voltaje y la corriente en una resistencia.
En circuitos lineales, el principio de superposición se aplica teniendo en cuenta lo siguiente:
-Hay que considerar cada fuente de voltaje independiente por separado y para ello es necesario apagar todas las demás. Basta con poner a 0 V todas las que no estén bajo análisis o bien sustituirlas en el esquema con un cortocircuito.
-Si la fuente es de corriente entonces hay que abrir el circuito.
-Cuando se considera la resistencia interna de las fuentes tanto de corriente como de voltaje, estas deben permanecer en su lugar, formando parte del resto del circuito.
-Si existen fuentes dependientes, deben quedar tal cual como aparecen en el circuito.
Índice del artículo
El teorema de superposición se utiliza para obtener circuitos más sencillos y fáciles de manejar. Pero debe tenerse presente siempre que solo aplica para aquellos con respuestas lineales, tal como se dijo al comienzo.
Entonces no se puede utilizar directamente para calcular la potencia por ejemplo, ya que la potencia está relacionada con la corriente mediante:
P =i2 R
Puesto que la corriente está elevada al cuadrado, la respuesta no es lineal. Tampoco es aplicable a circuitos magnéticos en los que intervienen transformadores.
Por otra parte, el teorema de superposición brinda la oportunidad de conocer el efecto que tiene cada fuente sobre el circuito. Y desde luego, mediante su aplicación es posible resolverlo completamente, es decir, conocer corrientes y voltajes a través de cada resistencia.
El teorema de superposición también puede usarse en conjunto con otros teoremas de circuito, por ejemplo el de Thévenin, para resolver configuraciones más complejas.
En circuitos de corriente alterna el teorema también es útil. En tal caso se trabaja con impedancias en vez de resistencias, siempre y cuando se pueda calcular la respuesta total de cada frecuencia de forma independiente.
Finalmente, en sistemas electrónicos el teorema es aplicable tanto para análisis en corriente directa como en corriente alterna, separadamente.
-Desactivar todas las fuentes independientes siguiendo las instrucciones dadas al comienzo, excepto la que se va a analizar.
-Determinar la salida, ya sea voltaje o corriente, que produce esa única fuente.
-Repetir los dos pasos descritos para todas las demás fuentes.
-Calcular la suma algebraica de todas las contribuciones halladas en los pasos anteriores.
Los ejemplos resueltos a continuación aclaran el uso del teorema en algunos circuitos sencillos.
En el circuito mostrado en la siguiente figura, encontrar la corriente que atraviesa cada resistencia mediante el teorema de superposición.
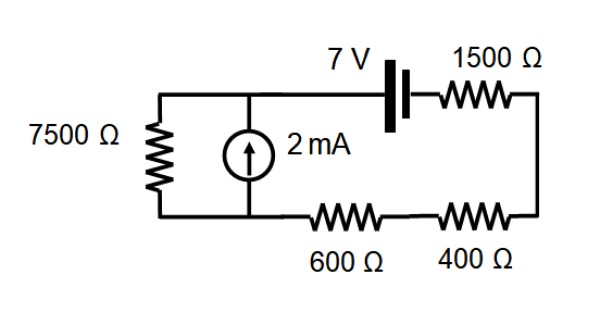
Solución
Contribución de la fuente de voltaje
Para comenzar se elimina la fuente de corriente, con lo cual el circuito queda de esta forma:
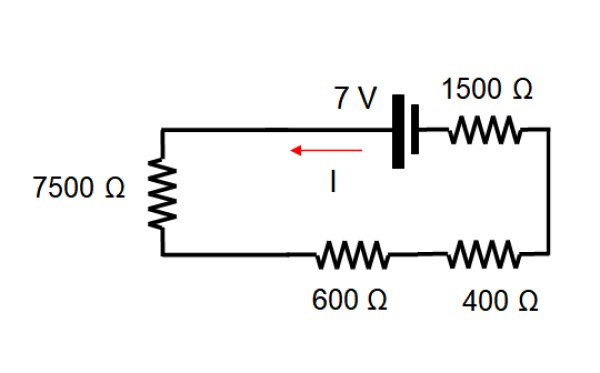
La resistencia equivalente se encuentra sumando el valor de cada resistencia, ya que todas están en serie:
7500 +600 +400 + 1500 Ω = 10.000 Ω
Aplicando la ley de Ohm V = I.R y despejando la corriente:
I = V/R = 7 / 10.000 A = 0.0007 A = 0.7 mA
Esta corriente es la misma para todas las resistencias.
Contribución de la fuente de corriente
Enseguida se elimina la fuente de voltaje, para trabajar únicamente con la fuente de corriente. El circuito resultante se muestra a continuación:
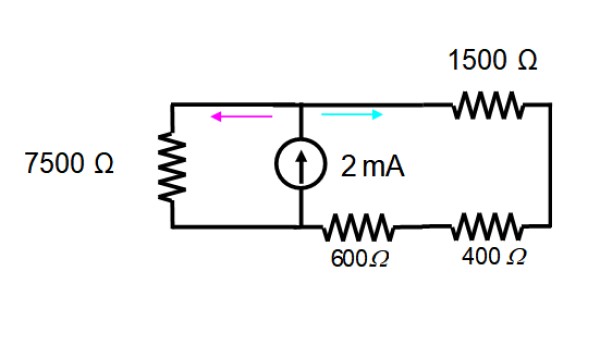
Las resistencias en la malla de la derecha están en serie y se pueden sustituir por una sola:
600 +400 + 1500 Ω =2500 Ω
El circuito resultante queda así:
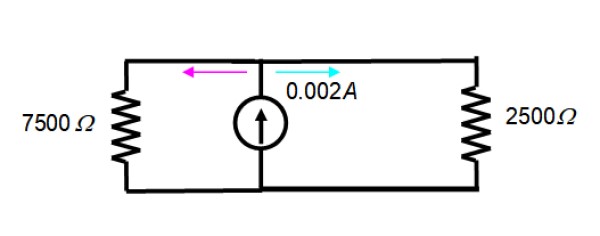
La corriente de 2 mA = 0.002 A se divide entre las dos resistencias de la figura, por lo tanto es válida la ecuación del divisor de corriente:
Ix = (Req/Rx)IT
Donde Ix es la corriente en la resistencia Rx, Req simboliza la resistencia equivalente e IT es la corriente total. Es preciso encontrar la resistencia equivalente entre ambas, sabiendo que:
1/Req = (1/ R1) + (1/ R2)
Por lo tanto:
1/Req = (1/7500) + (1/2500) = 1 / 1875 → Req = 1875 Ω
Para este otro circuito, la corriente que pasa a través de la resistencia de 7500 Ω se encuentra sustituyendo valores en la ecuación del divisor de corriente:
I7500 Ω = (1875/7500). 0.002 A = 0.0005 A = 0.5 mA
Mientras que la que pasa a través de la resistencia de 2500 Ω es:
I2500 Ω = 2 mA – 0.5 mA = 1.5 mA
Aplicación del teorema de superposición
Ahora se aplica el teorema de superposición para cada resistencia, comenzando por la de 400 Ω:
I400 Ω = 1.5 mA – 0.7 mA = 0.8 mA
Importante: para esta resistencia, las corrientes se restan, pues circulan en sentido contrario, según se desprende de la observación cuidadosa de las figuras, en las cuales los sentidos de las corrientes tienen colores diferentes.
Esta misma corriente atraviesa por igual a las resistencias de 1500 Ω y 600 Ω, puesto que todas están en serie.
Seguidamente se aplica el teorema para encontrar la corriente a través de la resistencia de 7500 Ω:
I7500 Ω = 0.7 mA + 0.5 mA = 1.2 mA
Importante: en el caso de la resistencia de 7500 Ω obsérvese que las corrientes se suman, porque en ambos circuitos circulan en el mismo sentido al pasar por esta resistencia. De nuevo es preciso observar atentamente los sentidos de las corrientes.
Encontrar la corriente y el voltaje a través de la resistencia de 12 Ω mediante el teorema de superposición.
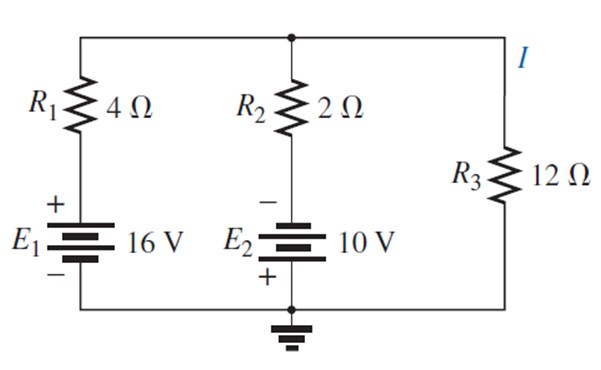
Solución
Se reemplaza la fuente E1 con un cortocircuito:
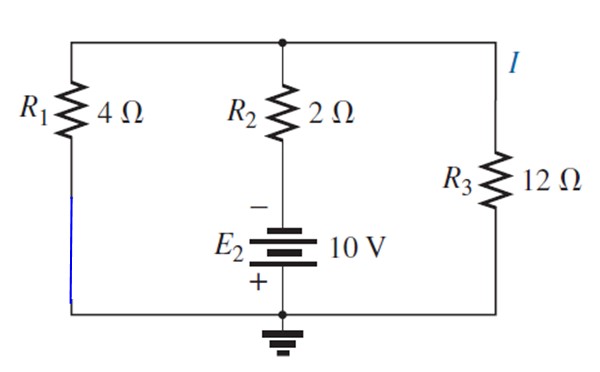
El circuito que resulta se dibuja de la siguiente forma, para visualizar fácilmente las resistencias que quedan en paralelo:
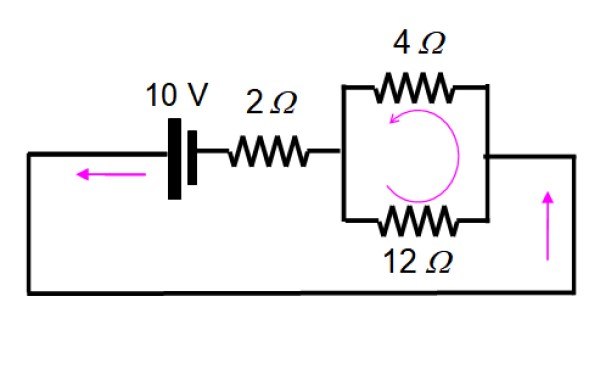
Y ahora se resuelve aplicando serie y paralelo:
1/Req = (1/12) + (1/4) = 1 / 3 → Req = 3 Ω
Esta resistencia a su vez está en serie con la de 2 Ω, por lo tanto la resistencia total es de 5 Ω. La corriente total es:
I = V/R = 10 V / 5 Ω = 2 A
Esta corriente se divide como:
I12Ω = (3/12)2 A = 0.5 A
Por lo tanto el voltaje es:
V12Ω = 0.5 A ×12 Ω = 6 V
Ahora se activa la fuente E1:
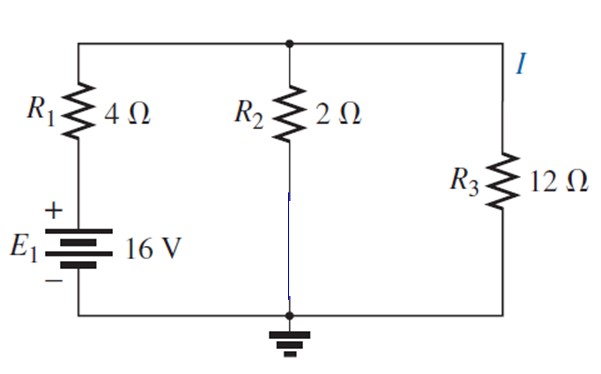
El circuito resultante se puede dibujar de esta manera:
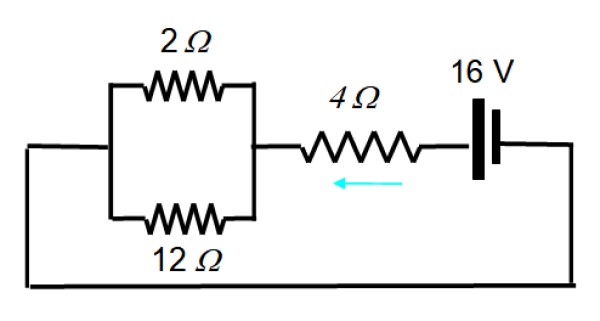
1/Req = (1/12) + (1/2) = 7 / 12 → Req = 12/7 Ω
Y en serie con la de 4 Ω resulta una resistencia equivalente de 40/7 Ω. En este caso la corriente total es:
I = V/R = 16 V / (40/7) Ω = 14/5 A
Se aplica nuevamente el divisor de tensión con estos valores:
I12Ω = ((12/7)/12) (14/5) A = 0.4 A
La corriente resultante es: 0.5 – 0.4 A = 0.1 A. Nótese que se han restado, pues la corriente de cada fuente tiene distinto sentido, como puede observarse en el circuito original.
El voltaje a través de la resistencia es:
V12Ω = 0.4 A ×12 Ω = 4.8 V
Finalmente, el voltaje total es: 6 V-4.8 V=1.2 V
- Alexander, C. 2006. Fundamentos de Circuitos Eléctricos. 3ra. Edición. Mc Graw Hill.
- Boylestad, R. 2011. Introducción al Análisis de Circuitos. 2da. Edición. Pearson.
- Dorf, R. 2006. Introduction to Electrical Circuits. 7th. Edition. John Wiley & Sons.
- Edminister, J. 1996. Circuitos Eléctricos. Serie Schaum. 3ra. Edición. Mc Graw Hill
- Wikipedia. Divisor de corriente. Recobrado de: es.wikipedia.org.
