Segunda ley de Newton: aplicaciones, experimentos y ejercicios
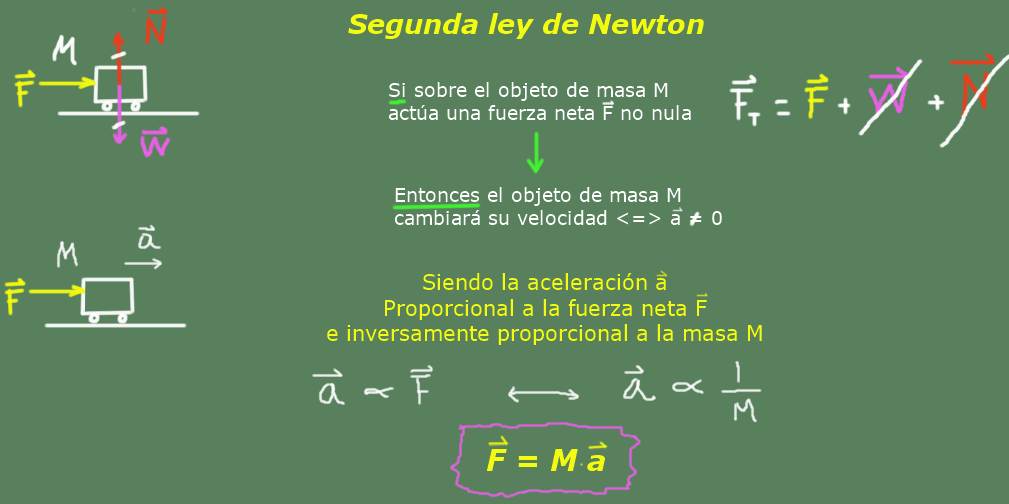
La segunda ley de Newton o ley fundamental de la dinámica establece que si un objeto está sometido a una fuerza o a un conjunto de fuerzas que no se anulan, entonces el objeto se acelerará en la dirección de la fuerza resultante, siendo esa aceleración proporcional a la intensidad de esa fuerza neta e inversamente proporcional a la masa del objeto.
Si F es la fuerza neta, M la masa del objeto y a la aceleración que adquiere, entonces la segunda ley de Newton se expresaría matemáticamente así: a = F / M o en la forma más usual F = M∙a
Índice del artículo
- 1 Explicación y fórmulas
- 2 Ejercicios resueltos
- 3 Aplicaciones de la segunda ley de Newton
- 4 Experimentos para niños
- 5 Artículos de interés
- 6 Referencias
Como se ha explicado anteriormente, la forma usual de expresar la segunda ley es con la fórmula:
F = M∙a
Tanto la aceleración como la fuerza tienen que estar medidos desde un sistema de referencia inercial. Nótese que la masa es una cantidad positiva, entonces la aceleración apunta en la misma dirección que la fuerza resultante.
Nótese también que cuando la fuerza resultante es nula (F = 0) entonces la aceleración también será nula ( a = 0 ) siempre que M > 0. Este resultado concuerda completamente con la primera ley de Newton o ley de inercia.
La primera ley de Newton establece los sistemas de referencias inerciales como aquellos que se trasladan con velocidad constante respecto a una partícula libre. En la práctica y para el propósito de las aplicaciones más comunes, un sistema de referencia fijo al suelo o cualquier otro que se mueva a velocidad constante respecto de ese, será considerado inercial.
La fuerza es la expresión matemática de la interacción del objeto con el entorno. La fuerza puede ser una cantidad constante o ir cambiando con el tiempo, la posición y la velocidad del objeto.
La unidad en el Sistema Internacional (SI) para la fuerza es el Newton (N). La masa en el (SI) se mide en (kg) y la aceleración en (m/s2). Un Newton de fuerza, es la fuerza necesaria para acelerar un objeto de 1 kg de masa a 1 m/s2 .
Un objeto de masa m se suelta desde cierta altura y se mide una aceleración de caída de 9,8 m/s².
Lo mismo ocurre con otro objeto de masa m’ y otro de masa m’’ y otro y otro. El resultado siempre es la aceleración de la gravedad que se denota con g y vale 9,8 m/s². En estos experimentos la forma del objeto y el valor de su masa es tal que la fuerza debida a la resistencia del aire es despreciable.
Se pide encontrar un modelo para la fuerza de atracción terrestre (conocida como peso) que sea consistente con los resultados experimentales.
Solución
Elegimos un sistema de referencia inercial (fijo respecto al piso) con dirección positiva del eje X vertical y hacia abajo.
La única fuerza que actúa sobre el objeto de masa m es la atracción terrestre, esa fuerza se denomina el peso P, como apunta hacia abajo es positiva.
La aceleración que adquiere el objeto de masa m una vez que se suelta es a=g , apuntado hacia abajo y positiva.
Planteamos la segunda ley de Newton
P = m a
cuál será el modelo de P de modo tal que la aceleración predicha por la segunda ley sea g independientemente del valor de m ? : La única alternativa es que P = m g siempre que m>0.
m g = m a de donde despejamos: a=g
Concluimos que el peso, la fuerza con la que la Tierra atrae a un objeto será la masa del objeto multiplicada por la aceleración de gravedad y su dirección es vertical y apuntado hacia abajo.
P = m∙g
Un bloque de 2 kg de masa reposa sobre un piso completamente liso y horizontal. Si se le aplica una fuerza de 1 N que aceleración adquiere el bloque y que velocidad tendrá al cabo de 1 s.
Solución
Lo primero es definir un sistema de coordenadas inercial. Se ha elegido uno con el eje X sobre el piso y el eje Y perpendicular al mismo. Luego se hace un diagrama de fuerzas, colocando las fuerzas debidas a las interacciones del bloque con su entorno.

La fuerza N representa la normal, es la fuerza vertical hacia arriba que la superficie del piso ejerce sobre el bloque M. Se sabe que N equilibra exactamente a P porque el bloque no se mueve en la dirección vertical.
F es la fuerza horizontal aplicada al bloque M, que apunta en la dirección positiva del eje X.
La fuerza neta es la suma de todas las fuerzas sobre el bloque de masa M. Se hace la suma vectorial de F, P y N. Como P y N son iguales y contrarias, se anulan entre si, y la fuerza neta es F.
De modo que la aceleración resultante será el cociente de la fuerza neta entre la masa:
a = F / M = 1 N / 2 kg = 0,5 m/s²
Como el bloque parte del reposo al cabo de 1s su velocidad habrá cambiado de 0 m/s a 0,5 m/s .
Un chico usa una báscula de baño para medir su peso. El valor que obtiene es de 50 kg. Luego el chico lleva la pesa al ascensor de su edificio, porque desea medir la aceleración de arrancada del ascensor. Los resultados obtenidos cuando arranca hacia arriba son:
- La báscula registra un peso de 58 kg durante 1,5 s
- Luego vuelve a medir 50 kg.
Con estos datos, calcule la aceleración del ascensor y la velocidad que adquiere.
Solución
La báscula mide el peso en una unidad llamada kilogramo_fuerza. Por definición, el kilogramo_fuerza es la fuerza con la que el planeta Tierra atrae a un objeto de 1 kg de masa.
Cuando la única fuerza que actúa sobre el objeto es su peso, entonces adquiere una aceleración de 9,8 m/s². Por lo que 1 kg_f equivale a 9.8 N.
El peso P del chico es entonces 50 kg*9.8m/s² = 490 N
Durante la aceleración la báscula ejerce una fuerza N sobre el chico de 58 kg_f equivalente a 58 kg * 9,8 m/s² = 568.4 N.
La aceleración del ascensor estará dada por:
a = N/M – g = 568.4 N / 50 kg – 9.8 m/s² = 1.57 m/s²
La velocidad adquirida por el ascensor después de 1.5 s con aceleración de 1.57 m/s² es:
v = a * t = 1.57 m/s² * 1.5 s = 2.36 m/s = 8.5 Km/h
La figura siguiente muestra un esquema de las fuerzas que actúan sobre el chico:
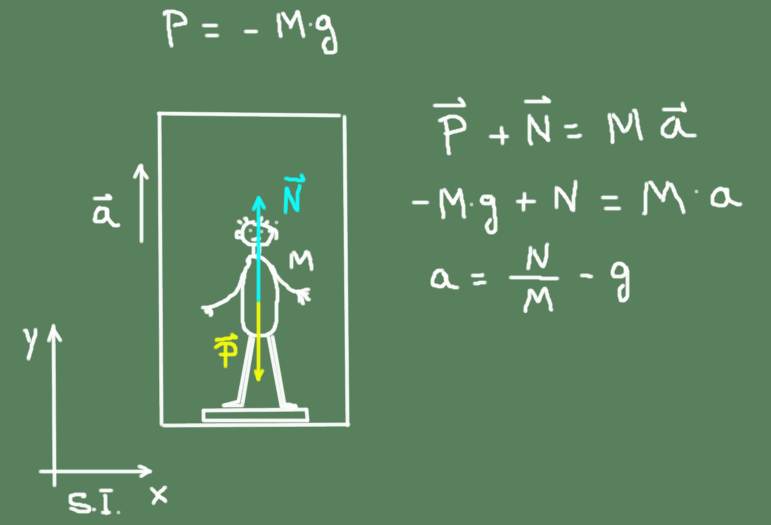
Un niño le pasa a su hermano el frasco de mayonesa a su hermano, que está al otro extremo de la mesa. Para eso la impulsa de forma tal que adquiere una velocidad de 3 m/s. Desde que suelta el frasco hasta que se detiene en el extremo opuesto de la mesa el recorrido fue de 1,5 m.
Determine el valor de la fuerza de fricción que la mesa ejerce sobre el frasco, sabiendo que el mismo tiene una masa de 0,45 kg.
Solución
En primer lugar determinaremos la aceleración de frenado. Para ello usaremos la siguiente relación, ya conocida del movimiento rectilíneo uniformemente acelerado:
Vf² = Vi² + 2 * a * d
donde Vf es la velocidad final, Vi la velocidad inicial, a la aceleración y d el desplazamiento.
La aceleración obtenida a partir de la relación anterior es, donde se ha tomado como positivo el desplazamiento del frasco.
a = ( 0 – 9 (m/s)² ) / (2*1.5 m) = -3 m/s²
La fuerza neta sobre el frasco de mayonesa es la fuerza de roce, ya que la normal y el peso del frasco se equilibran: Fneta = Fr.
Fr = m * a = 0.45 kg * (-3 m/s²) = -1.35 N = -0.14 kg-f
Los niños y también los adultos pueden llevar a cabo experiencias sencillas que les permiten comprobar que la segunda ley de Newton realmente funciona en la vida real. Aquí hay dos bien interesantes:
Un experimento sencillo requiere una báscula de baño y un ascensor. Lleve una pesa de baño a un ascensor y registre los valores que marca durante el arranque de subida, el arranque de bajada y durante el lapso que se mueve a velocidad constante. Calcule las aceleraciones del ascensor correspondientes a cada caso.
- Tome un carrito de juguete que tenga sus ruedas bien lubricadas
- Sujete una cuerda al extremo.
- En el borde de la mesa asegure con cinta adhesiva un lápiz, u otro objeto cilíndrico y liso sobre el cual pasará la cuerda.
- Al otro extremo de la cuerda cuelgue una pequeña canasta, a la cual colocará unas monedas o algo que sirva de peso.
El esquema del experimento se muestra a continuación:
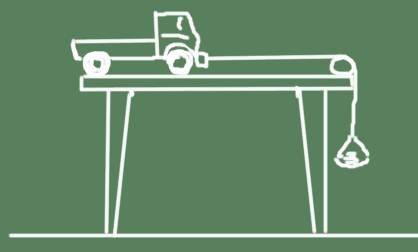
- Suelte el carrito y observe como se acelera.
- A continuación aumente la masa del carrito colocando monedas sobre él, o algo que aumente su masa.
- Diga si la aceleración aumenta o disminuye. Coloque más masa sobre el carrito, observe como se acelera y concluya.
A continuación se deja el carrito sin peso extra y se le deja que acelere. Entonces se lo coloca más peso sobre la canasta con el fin de aumentar la fuerza aplicada al carrito.
- Compare la aceleración con el caso anterior, indique si aumenta o disminuye. Puede repetir añadiendo más peso a la canasta y observar la aceleración del carrito.
- Indicar si aumenta o disminuye.
- Analice sus resultados y diga si concuerdan o no con la segunda ley de Newton.
Ejemplos de la segunda ley de Newton.
Ejemplos de la segunda ley de Newton.
- Alonso M., Finn E. 1970. Física volumen I: Mecánica. Fondo Educativo Interamericano S.A. 156-163.
- Hewitt, P. 2012. Conceptual Physical Science. Fifth edition. 41-46.
- Young, Hugh. 2015. University Physics with Modern Physics. 14th Ed. Pearson. 108-115.
