Medición aproximada de figuras amorfas: ejemplo y ejercicio

La medición aproximada de las figuras amorfas consiste en una serie de métodos utilizados para determinar el área o el perímetro de figuras geométricas que no son triángulos, cuadrados, círculos, etc. Algunos  son extensibles a figuras tridimensionales.

Básicamente la medición consiste en hacer un reticulado de alguna forma regular, como rectángulos, cuadrados o trapecios, que cubran aproximadamente la superficie. La precisión de la aproximación del área obtenida por estos métodos aumenta con la finura o densidad del reticulado.

Las figuras 1 y 2 muestran diversas figuras amorfas. Para calcular el área se ha efectuado un reticulado, compuesto de cuadrados de 2 X 2, los cuales a su vez están subdivididos en veinticinco cuadraditos de 2/5 x 2/5.

Sumando las áreas de los cuadrados principales y los cuadrados secundarios se obtiene el área aproximada de la figura amorfa.

Índice del artículo

• 1 Área bajo una curva
  • 1.1 Intervalos regulares
• 2 Ejemplo
• 3 Ejercicio resuelto
• 4 Referencias

Área bajo una curva

Frecuentemente es necesario calcular aproximadamente el área bajo una curva entre dos valores límites. En este caso, en vez de un reticulado cuadrado, pueden trazarse franjas rectangulares que cubran en forma aproximada el área bajo la dicha curva.

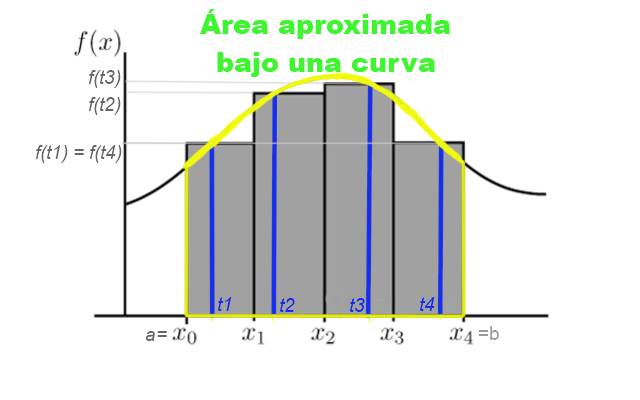
La suma de todas las franjas rectangulares recibe el nombre de suma o sumatoria de Riemann. La figura 3 muestra una partición del intervalo [a, b] sobre el que se quiere determinar en forma aproximada el área bajo la curva.

Supongamos que se quiere calcular el área bajo la curva dada por la función y = f(x), donde x pertenece al intervalo [a, b] dentro del cual se quiere calcular el área. Para esto se efectúa una partición de n elementos dentro de este intervalo:

Partición = {x0= a, x1, x2, …, xn= b}.

Entonces el área aproximada bajo la curva dada por y = f(x) en el intervalo [a, b] se consigue efectuando la siguiente sumatoria:

S = ∑_k=1ⁿ f(t_k) (x_k – x_k-1)

Donde t_k está comprendido entre x_k-1 y x_k: x_k-1 ≤ t_k ≤ x_k .

En la figura 3 se muestra gráficamente la sumatoria de Riemann de la curva y = f(x) en el intervalo [x0, x4]. En este caso se hizo una partición de cuatro subintervalos y la suma representa el área total de los rectángulos grises. 

Esta suma representa una aproximación al área bajo la curva f entre las abscisas x=x0 y x=x4.

La aproximación al área bajo la curva mejora en la medida que el número n de particiones sea mayor, y tiende a ser exactamente el área bajo la curva cuando el número n de particiones tiende a infinito. 

En caso que la curva está representada por una función analítica, los valores f(t_k) se calculan evaluando dicha función en los valores t_k. Pero si la curva no tiene una expresión analítica, entonces quedan las siguientes posibilidades:

1. Aproximar la curva por una función, por ejemplo un polinomio.
2. Tomar las coordenadas cartesianas de los puntos donde la curva se intercepta con las rectas x = t_k.

Intervalos regulares

Dependiendo de la elección del valor tk en el intervalo [x_k, x_k-1], la suma puede sobreestimar o subestimar el valor exacto del área bajo la curva de la función y = f(x). Lo más aconsejable es tomar el punto tk donde el área faltante sea aproximadamente igual al área sobrante, aunque no siempre es posible efectuar tal elección.  

Tomar tk en el extremo derecho

Lo más práctico entonces es usar intervalos regulares de ancho Δx = (b – a)/n, donde a y b son los valores mínimo y máximo de la abscisa, mientras que n es el número de subdivisiones.

En ese caso el área bajo la curva se aproxima por:

Área = {f(a+Δx) +f(a+2Δx)+ …+ f[a+(n-1]Δx+f(b)}*Δx

En la expresión anterior, tk se tomó en el extremo derecho del subintervalo.

Tomar tk en el extremo izquierdo

Otra posibilidad práctica es tomar el valor tk en el extremo izquierdo, en cuyo caso la suma que aproxima el área se expresa como:

Área = [f(a) +f(a+Δx)+ …+f(a+(n-1)Δx)]*Δx

Tomar tk como valor central

En caso que tk se elija como el valor central del subintervalo regular de ancho Δx, la suma que aproxima el área bajo la curva es:

Área = [f(a+ Δx/2) +f(a+ 3Δx/2)+ …+f(b- Δx/2 )]*Δx

Cualquiera de estas expresiones tiende al valor exacto en la medida que el número de subdivisiones sea arbitrariamente grande, es decir que Δx tienda a cero, pero en este caso el número de términos de la sumatoria se hace inmensamente grande con el consiguiente costo computacional. 

Ejemplo

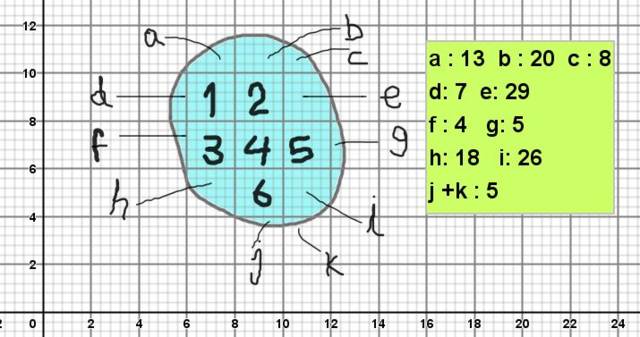
La figura 2 muestra una figura amorfa, cuyo contorno es semejante a las piedras de la imagen 1. Para calcular su área se la coloca sobre un reticulado con cuadrados principales de 2 x 2 unidades al cuadrado (por ejemplo pueden ser de 2 cm²).

Y como cada cuadrado está subdividido en 5 x 5 subdivisiones, entonces cada subdivisión tiene un área de 0,4 x 0,4 unidades al cuadrado ( 0,16 cm² ).

El área de la figura se calcularía así:

Área = 6 x 2 cm² + (13 + 20 + 8 + 7 + 29 + 4 + 5 + 18 + 26 + 5) x 0,16 cm²

Es decir:

Área = 12 cm² + 135 x 0,16 cm² = 33,6 cm².

Ejercicio resuelto

Calcular aproximadamente el área bajo la curva dada por la función f(x) = x² entre a = -2 hasta b = +2. Para ello escribir primero la suma para n particiones regulares del intervalo [a, b] y luego tomar el límite matemático para el caso que el número de particiones tienda a infinito. 

Solución

En primer lugar se define el intervalo de las particiones como 

Δx = (b – a)/n. 

Luego la suma por la derecha correspondiente a la función f(x) queda así:

[-2 +(4i/n)]² = 4 – 16 i /n + (4/n)² i²

Y luego se sustituye en la sumatoria:

Y la tercera resulta:

S(f, n) = 16 – 64(n+1)/2n + 64(n+1)(2n+1)/6n²

Al escoger un valor grande para n se tiene una buena aproximación al área bajo la curva. Sin embargo, en este caso es posible conseguir el valor exacto tomando el límite matemático cuando n tienda a infinito:

Área = lim_n->∞[16 – 64(n+1)/2n + 64(n+1)(2n+1)/6n²]

Área = 16 – (64/2)+ (64/3) = 16/3 = 5,333.

Referencias

1. Casteleiro, J. M. 2002. Cálculo integral (Edición ilustrada). Madrid: ESIC Editorial.
2. Larson, R. 2010. Cálculo de una variable. 9na. Edición. McGraw Hill.
3. Purcell, E. 2007. Cálculo con Geometría Analítica. 9na. Edición. Pearson Educación.
4. Unican. Historia del concepto de integral. Recuperado de: repositorio.unican.es
5. UIS. Sumas de Riemann. Recuperado de: matematicas.uis.edu.co
6. Wikipedia. Área. Recuperado de: es.wikipedia.com