Factor de compresibilidad: cómo calcular, ejemplos y ejercicios

El factor de compresibilidad Z, o factor de compresión para los gases, es un valor adimensional (sin unidades) que se introduce a modo de corrección en la ecuación de estado de los gases ideales. De esta manera el modelo matemático se asemeja más al comportamiento observado del gas.

En el gas ideal, la ecuación de estado que relaciona a las variables P (presión), V (volumen) y T (temperatura) es: P.V _ideal = n.R.T con n = número de moles y R = constante de los gases ideales. Añadiendo la corrección del factor de compresibilidad Z, esta ecuación se transforma en:

P.V= Z.n.R.T

Índice del artículo

• 1 ¿Cómo calcular de factor de compresibilidad?
• 2 Ejemplos
  • 2.1 El factor de compresibilidad en gases ideales, aire, hidrógeno y agua
• 3 Ejercicios resueltos
  • 3.1 Ejercicio 1
  • 3.2 Ejercicio 2
• 4  Referencias

¿Cómo calcular de factor de compresibilidad?

Tomando en cuenta que el volumen molar es V_molar = V/n, se tiene el volumen molar real:

P . V_real = Z. R. T → Z = PV _real/RT

Ya que el factor de compresibilidad Z depende de las condiciones del gas, se expresa como función de la presión y la temperatura:

Z = Z(P,T)

Comparando las dos primeras ecuaciones se advierte que si el número de moles n es igual a 1, el volumen molar de un gas real está relacionado con el del gas ideal mediante:

 V_real / V_ideal = Z →  V _real = Z V_ideal

Cuando la presión sobrepasa las 3 atmósferas la mayor parte de los gases deja de comportarse como gases ideales y el volumen real difiere significativamente del ideal.

De esto se percató en sus experimentos el físico holandés Johannes Van der Waals (1837-1923), lo cual le llevó a crear un modelo que se ajustaba mejor a los resultados prácticos que la ecuación de los gases ideales: la ecuación de estado de Van der Waals.

Ejemplos

Según la ecuación P.V_real= Z.n.RT, para un gas ideal, Z = 1. Sin embargo, en los gases reales, al aumentar la presión también lo hace el valor de Z. Esto tiene sentido porque a mayor presión las moléculas de gas tienen más oportunidades para colisionar, por lo tanto las fuerzas de repulsión aumentan y con ello el volumen.

En cambio a presiones más bajas, las moléculas se mueven con mayor libertad y las fuerzas de repulsión disminuyen. Por lo tanto se espera un volumen menor. En cuanto a la temperatura, cuando esta aumenta, Z disminuye.

Tal como observó Van der Waals, en las cercanías del llamado punto crítico, el comportamiento del gas se desvía mucho del de un gas ideal.

El punto crítico (T_c, P_c) de una sustancia cualquiera son los valores de presión y temperatura que determinan su comportamiento ante un cambio de fase:

-T_c es la temperatura por encima de la cual el gas en cuestión no se licua.

-P_c  es la presión mínima requerida para licuar el gas a temperatura T_c

Cada gas tiene un punto crítico propio, sin embargo, definiendo la temperatura y la presión reducida T_r y P_r de la siguiente forma:

P_r = P / P_c

V_r = V /V_c

T_r = T /T_c

Se observa que un gas confinado con idénticas V_r y T_r ejerce la misma presión P_r. Por este motivo, si se grafica Z en función de P_r a una misma T_r, cada punto en dicha curva es el mismo para cualquier gas. A esto se le denomina principio de estados correspondientes.

El factor de compresibilidad en gases ideales, aire, hidrógeno y agua

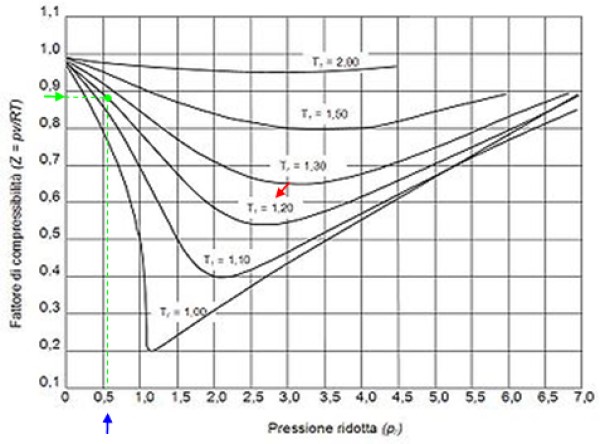
A continuación se tiene una curva de compresibilidad para varios gases a distintas temperaturas reducidas. Seguidamente algunos ejemplos de Z para algunos gases y un procedimiento para encontrar Z mediante el uso de la curva.

Gases ideales

Los gases ideales tienen Z=1, como se explicó al comienzo.

Aire

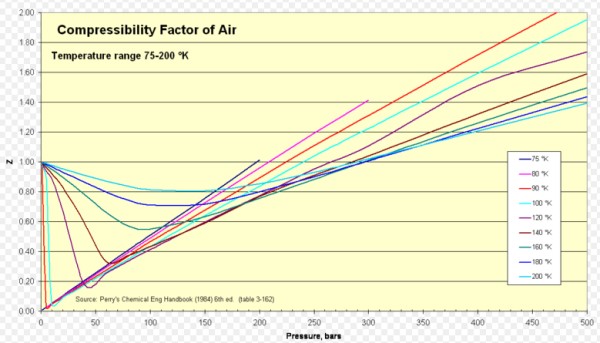
Para el aire Z es aproximadamente 1 en un extenso rango de temperaturas y presiones (ver figura 1), donde el modelo de gas ideal da muy buenos resultados.

Hidrógeno

Z > 1 para todas las presiones.

Agua

Para hallar Z del agua se necesitan los valores del punto crítico. El punto crítico del agua es: P_c = 22.09 MPa y T_c= 374.14 ° C (647.3 K). De nuevo es preciso tener en cuenta que el factor de compresibilidad Z depende de la temperatura y la presión.

Por ejemplo, supongamos que se quiere encontrar Z del agua a 500 ºC y 12 MPa. Entonces lo primero es calcular la temperatura reducida, para lo cual hay que pasar a kelvin los grados centígrados: 50 ºC = 773 K:

T_r = 773 / 647.3 = 1.2

P_r = 12 / 22.09 = 0.54

Con estos valores ubicamos en la gráfica de la figura la curva correspondiente a T_r = 1.2, señalada con una flecha roja. Seguidamente buscamos en el eje horizontal el valor de P_r más cercano a 0.54, marcado en azul. Ahora trazamos una vertical hasta interceptar a la curva T_r = 1.2 y por último se proyecta desde ese punto hasta el eje vertical, donde leemos el valor aproximado de Z = 0.89.

Ejercicios resueltos

Ejercicio 1

Se tiene una muestra de gas a temperatura de 350 K y una presión de 12 atmósferas, con un volumen molar 12 % mayor al predicho por la ley de los gases ideales. Calcular:

a) Factor de compresión Z.

b) Volumen molar del gas.

c) Según los resultados anteriores, señale cuales son las fuerzas dominantes en esta muestra de gas.

Dato: R = 0,082 L.atm/mol.K

Solución a

Sabiendo que V _real  es 12 % mayor que V_ideal :

 V_real  = 1.12V_ideal

Z = V _real / V_ideal = 1.12

Solución b

P . V_real = Z. R. T→ V_real = (1.12 x 0.082 x 350 /12 )L/mol = 2.14 L/mol.

Solución c

Las fuerzas de repulsión son las que predominan, ya que el volumen de la muestra se incrementó.

Ejercicio 2

Se tienen 10 moles de etano confinados en un volumen de 4.86 L a 27 ºC. Encontrar la presión ejercida por el etano a partir de:

a) El modelo de gas ideal

b) La ecuación de van der Waals

c) Halle el factor de compresión a partir de los resultados anteriores.

Datos para el etano

Coeficientes de Van der Waals:

a = 5.489 dm⁶. atm . mol^-2  y b = 0.06380 dm³. mol^-1.

Presión crítica: 49 atm. Temperatura crítica: 305 K

Solución a

Se pasa la temperatura a kelvin: 27 º C = 27 +273 K = 300 K, recordar asimismo que 1 litro = 1 L = 1 dm³.

Luego se sustituyen los datos suministrados en la ecuación del gas ideal:

P.V = n.R.T → P = (10 x  0,082 x 300 / 4.86 L) atm = 50.6 atm

Solución b

La ecuación de estado de Van der Waals es:

Donde a y b son los coeficientes dados por el enunciado. Al despejar P:

Solución c

Calculamos la presión y la temperatura reducidas:

P_r = 35.2/ 49 = 0.72

T_r = 300 /305 = 0.98 ≈ 1

Con estos valores se busca el valor de Z en la gráfica de la figura 2, encontrando que Z es aproximadamente 0.7.

 Referencias

1. Atkins, P. 1999. Química Física. Ediciones Omega.
2. Cengel, Y. 2012. Termodinámica. 7^ma Edición. McGraw Hill.
3. Engel, T. 2007. Introducción a la Fisicoquímica: Termodinámica. Pearson.
4. Levine, I. 2014. Principios de Físico-química. 6ta. Edición. McGraw Hill.
5. Wikipedia. Compressibility Factor. Recuperado de: en.wikipedia.org.