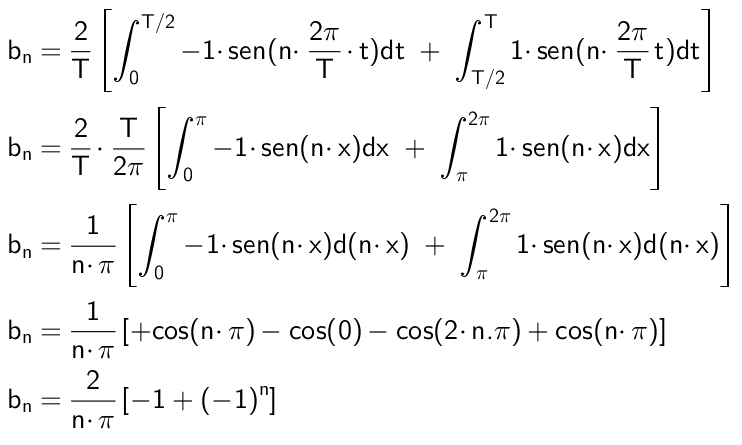Series de Fourier: aplicaciones, ejemplos y ejercicios resueltos
Las series de Fourier consisten en una sumatoria de infinitos términos, los cuales constan de funciones armónicas, seno y coseno, cuyo argumento es múltiplo entero de una frecuencia fundamental.
Las funciones seno y coseno están multiplicadas por coeficientes de valores, tales que la sumatoria es idéntica a una función con periodo T igual a dos veces pi (2π) dividido entre la frecuencia angular fundamental ω.
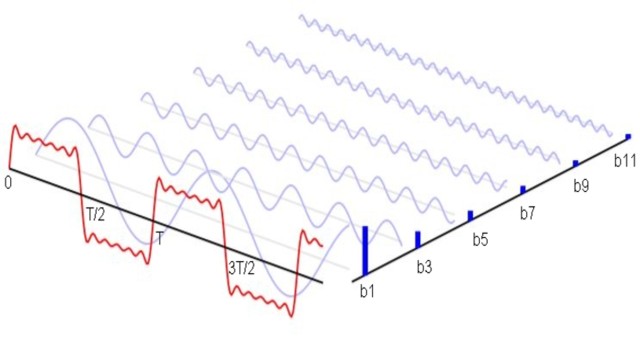
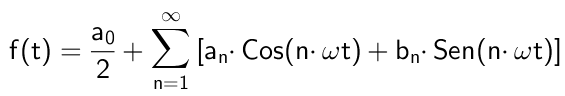
Donde ω es la frecuencia fundamental, que se relaciona con el período T de la función f(t) mediante la relación:
ω = 2π / T
Por ser periódica de período T, la función f(t) cumple esta condición:
f(t) = f(t + k T)
Donde k es un número entero y los coeficientes a0 , an y bn se denominan los coeficientes de Fourier.
Índice del artículo
- 1 Importancia y usos de las series de Fourier
- 2 Ejemplo de serie de Fourier
- 3 Ejercicios
- 4 Referencias
El nombre de series de Fourier se debe a que su descubridor fue el matemático francés Jean Baptiste Joseph Fourier, quien las publicó entre 1807 y 1811, cuando buscaba la manera de resolver la ecuación de calor.
Este descubrimiento fue fundamental para las Matemáticas, ya que si una ecuación diferencial tiene una solución particular armónica, entonces es posible conseguir la solución general mediante la superposición o sumatoria de la mismas.
Los coeficientes de Fourier de una función periódica, también llamada señal, son el espectro de la misma.
Por lo tanto, el espectro es el conjunto de frecuencias que conforman una señal caracterizado por la amplitud de cada frecuencia, lo cual se corresponde con los valores de los coeficientes de Fourier.
Los sistemas de compresión de señales o formas de onda de audio y video, en el fondo lo que hacen es guardar en una memoria los coeficientes de Fourier, ya que el conocimiento de los mismos permite reconstruir la señal original, con la ventaja que ocupan un número significativamente menor de bits que la señal original digitalizada.
La serie de Fourier de una señal es como su huella digital, en el sentido que, conocidos los coeficientes que la conforman, siempre se puede saber a qué señal pertenecen.
Aunque el uso de la serie de Fourier, o su forma más general, la transformada de Fourier, como método de compresión de señales se conoce desde hace bastante tiempo, su uso en la práctica tuvo que esperar por procesadores numéricos lo suficientemente rápidos, que permitieran que las señales fuesen comprimidas y descomprimidas en “tiempo real”.
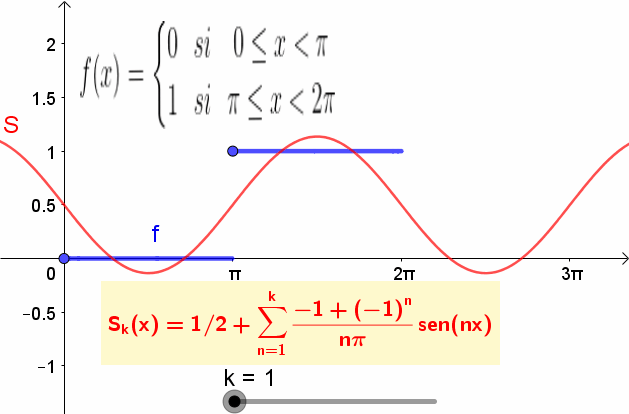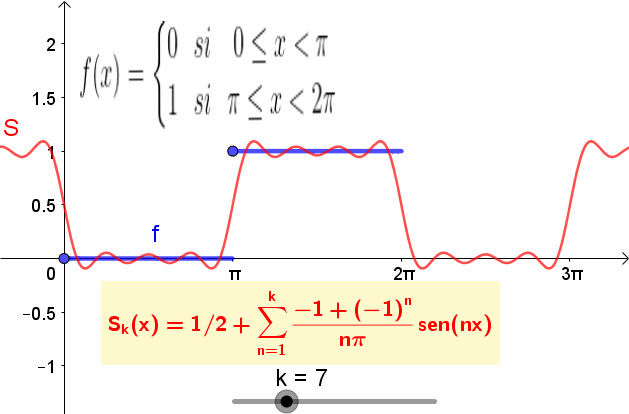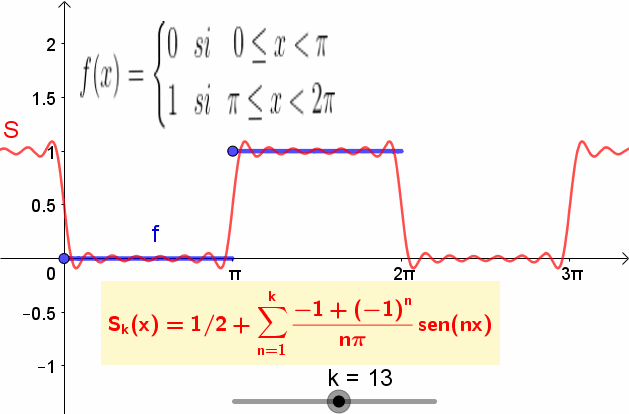
A continuación se da un ejemplo de función f(t) y su serie de Fourier.
La función es:
f(t) = { 0 si 0 ≤ t π y 1 si π ≤ t 2π }
Y tiene su correspondiente serie de Fourier dada por:
f(t) = ½ – 2/π⋅Sen(t) – 2/(3π)⋅Sen(3t) – 2/(5π)⋅Sen(5t) – 2/(7π)⋅Sen(7t) – …..
La siguiente figura muestra la función y la suma parcial de la serie de Fourier:
A continuación se muestra cómo determinar los coeficientes de Fourier:
Supongamos que la función sea f(x) definida en un intervalo que va desde ti hasta ti + T, donde T mayúscula será el periodo de la función. Entonces su serie de Fourier es:
f(t) = a₀/2 + a₁ Cos(ω t) + a₂ Cos(2 ω t) + …+an Cos( n ω t) + …..
………….+ b₁ Sen(ω t) + b₂ Sen(2 ω t) + …+bn Sen( n ω t) +……
Cálculo del término independiente
Para hallar el término independiente integramos ambos miembros de la igualdad en el intervalo de definición de la función:
[ti , ti+ T]
Por lo tanto:
∫ f(t) dt = a₀/2 ∫dt + a₁ ∫Cos(ω t) dt + a₂ ∫Cos(2 ω t) dt + …+an ∫Cos( n ω t) dt + …..
………….+ b₁ ∫Sen(ω t) dt + b₂ ∫Sen(2 ω t) dt + …+bn ∫Sen( n ω t) dt +……
Acá el símbolo ∫ significa integral definida desde ti hasta ti + T.
La integral del primer término es t, que al ser evaluada en su límite superior resulta:
ti + T
Al restar el límite inferior ti, da en definitiva T.
Todos los otros términos son 0, porque se trata de funciones coseno o seno evaluadas en un periodo completo, como mostramos a continuación:
∫Cos(nω t) dt = (1/ nω) ∫Cos(nω t) d(nω t)
Recuerde que el símbolo ∫ significa integración entre ti hasta ti + T.
Para efectuar la integración de los términos que tienen coseno o seno haremos el siguiente cambio de variable:
x = ω (t – ti)
De modo que el diferencial de x, dx es igual al diferencial de d(ωt).
Entonces la integral a efectuar es:
Por lo tanto, la integral definida evaluada en un periodo completo de todos los términos que contienen seno o coseno es 0 y el único término no nulo es el que contiene el coeficiente a₀.
Se concluye por tanto que el término a₀ se calcula así:
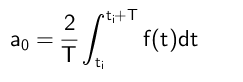
Cálculo de los coeficientes a’s
Para calcular los coeficientes a’s que multiplican a las funciones coseno, hay que multiplicar ambos miembros de la igualdad:
f(t) = a₀/2 + a₁ Cos(ω t) + a₂ Cos(2 ω t) + …+an Cos( n ω t) + …..
………….+ b₁ Sen(ω t) + b₂ Sen(2 ω t) + …+bn Sen( n ω t) +……
Por la función coseno evaluada en el armónico correspondiente y luego se procede a aplicar la integral definida en un periodo completo a ambos miembros.
Por ejemplo, para calcular am se procede a multiplicar ambos miembros por Cos(mωt):
f(t) Cos( m ω t) = a₀/2 Cos( m ω t) + a₁ Cos(ω t) Cos( m ω t) + a₂ Cos(2 ω t) Cos( m ω t) + …+an Cos( n ω t) Cos( m ω t) + …..
………….+ b₁ Sen(ω t) Cos( m ω t) + b₂ Sen(2 ω t) Cos( m ω t) + …+bn Sen( n ω t) Cos( m ω t) +……
Luego se integra en un periodo completo, es decir en el intervalo que va desde ti hasta ti + T.
La integral del término que contiene a₀ se anula, porque m es un número entero y se está integrando la función coseno en un periodo completo.
Las integrales que contienen el producto Cos( n ω t) Cos( m ω t) también se anulan siempre que n≠m. Solo en el caso que n=m se tiene la integral:
De aquí se concluye que:
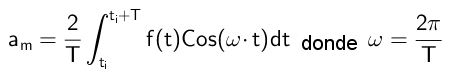
Cálculo de los coeficientes b’s
Para hallar los coeficientes b’s se aplica un procedimiento similar, pero esta vez se multiplican ambos miembros de la función igualada a la serie de Fourier completa por la función sen(m ω t).
Por las mismas razones ya explicadas para el caso en el que se multiplicaba por el coseno, el único término que no se anula después de integrar en un periodo completo es aquel en el cual:
n=m
Y donde aparece la integral de [Sen(m ω t)]2, que integrada sobre un periodo completo da como resultado π.
De esta forma, los coeficientes b’s se calculan de acuerdo a la siguiente fórmula:

Hacer el cálculo explícito de los coeficientes de la función
f(t) = { 0 si 0 ≤ t π y 1 si π ≤ t 2π }
Solución
En primer lugar identificamos el período T de esta función como 2π, por lo que la frecuencia fundamental ω = 2π/ T en este ejemplo es igual a la unidad, es decir:
ω = 1
La función está definida en el intervalo [0, 2π], por lo que todas las integraciones se realizarán en dicho intervalo.
Entonces el término independiente se calcula de la siguiente manera:
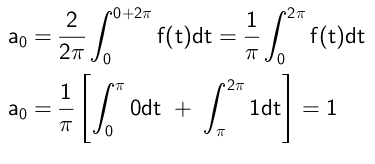
Los coeficientes que multiplican a las funciones coseno se calculan de esta forma:
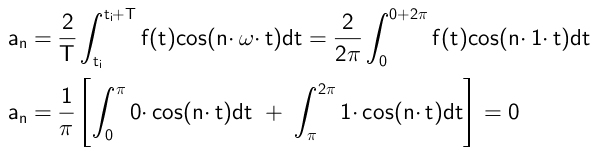
Como puede verse, todos los coeficientes a´s son nulos, lo cual ocurrirá siempre que la función f(t) sea impar.
De forma semejante los coeficientes b’s se calcularán de la siguiente manera:
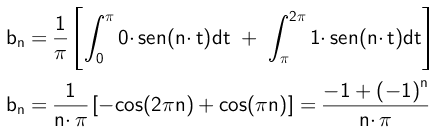
Hallar los coeficientes de la función correspondiente a la figura 1, la cual es:
f(t) = { -1 si 0≤ t Como la función toma valores comprendidos entre -1 y +1, podemos intuir que el término independiente es nulo, sin embargo lo calcularemos explícitamente: Por el hecho que la función tiene simetría impar, todos los coeficientes a’s que multiplican a los términos armónicos con la función coseno deben ser nulos. Lo verificamos a continuación: Por último, hallaremos los coeficientes b’s que multiplican a los términos armónicos que contienen la función seno: De donde puede notarse que todos los términos b’s con subíndice par son 0. Los primeros términos impares son: b1= -4/(π); b3= -4/(3π); b5= -4/(5π); b7= -4/(7π) y b9= -4/(9π)Solución