Trapecio rectángulo: propiedades, relaciones y fórmulas, ejemplos
Un trapecio rectángulo es una figura plana de cuatro lados, tal que dos de ellos son paralelos entre sí, denominados bases y además uno de los otros lados es perpendicular a las bases.
Por este motivo, dos de los ángulos internos son rectos, es decir, miden 90º. De allí el nombre de “rectángulo” que se le da a la figura. La siguiente imagen de un trapecio rectángulo aclara estas características:
Índice del artículo
- 1 Elementos del trapecio
- 2 Relaciones y fórmulas
- 3 Ejemplos de trapecios rectángulos
- 4 Ejercicios resueltos
- 5 Referencias
Los elementos del trapecio son:
-Bases
-Vértices
-Altura
-Ángulos internos
-Base media
-Diagonales
Vamos a detallar estos elementos con ayuda de las figuras 1 y 2:
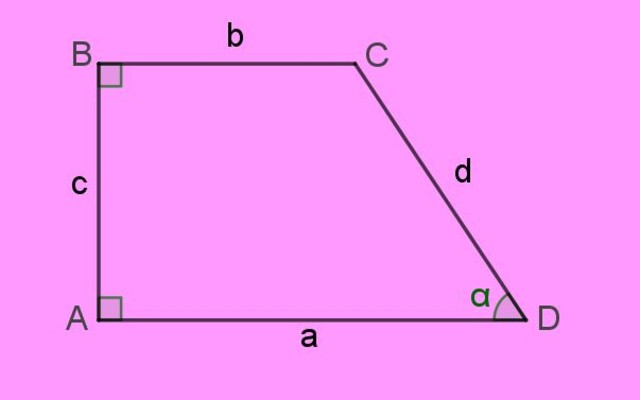
Los lados del trapecio rectángulo se denotan mediante letras minúsculas a, b, c y d. Las esquinas de la figura o vértices se indican en mayúsculas. Finalmente los ángulos internos están expresados con letras griegas.
Según la definición, las bases de este trapecio son los lados a y b, que como se observa son paralelos y además tienen diferente longitud.
El lado perpendicular a ambas bases es el lado c a la izquierda, que es la alturah del trapecio. Y por último está el lado d, que forma el ángulo agudo α con el lado a.
La suma de los ángulos internos de un cuadrilátero es 360º. Se aprecia fácilmente que el ángulo C faltante en la figura es 180 – α.
La base media es el segmento que une los puntos medios de los lados no paralelos (segmento EF en la figura 2).
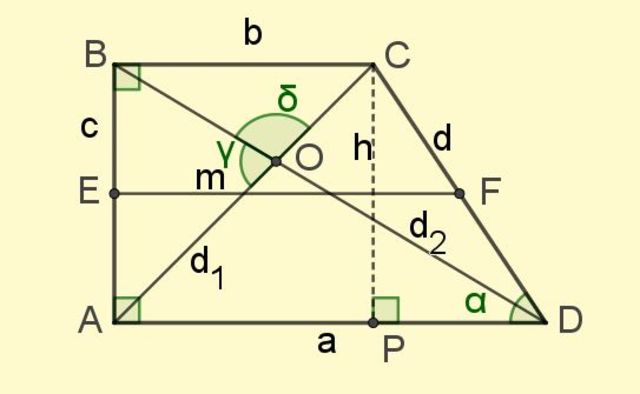
Y por último están las diagonales d1 y d2, los segmentos que unen a los vértices opuestos y que se intersectan en el punto O (ver figura 2).
h = c
Es la medida del contorno y se calcula sumando los lados:
Perímetro = a + b + c + d
El lado d se expresa en términos de la altura o el lado c mediante el teorema de Pitágoras:
d = √(a-b)2 + c2
Sustituyendo en el perímetro:
P = a + b + c + √(a-b)2 + c2
Es la semisuma de las bases:
Base media = (a+b)/2
A veces se encuentra la base media expresada de esta forma:
Base media = (Base mayor + base menor) /2
El área A del trapecio es el producto de la base media por la altura:
A =(Base mayor + base menor) x altura /2
A = (a+b)c/2
En la figura 2 aparecen varios triángulos, tanto rectángulos como no rectángulos. A los que son triángulos rectángulos se les puede aplicar el teorema de Pitágoras y a los que no, los teoremas del coseno y del seno.
De esta forma se encuentran relaciones entre los lados y entre los lados y los ángulos internos del trapecio.
Triángulo CPA
Es rectángulo, sus catetos son iguales y valen b, mientras que la hipotenusa es la diagonal d1, por lo tanto:
d12 = b2 + b2 = 2b2
Triángulo DAB
También es rectángulo, los catetos son a y c (o también a y h) y la hipotenusa es d2, de manera que:
d22 = a2 + c2 = a2 + h2
Triángulo CDA
Como este triángulo no es rectángulo, se le aplica el teorema de coseno, o también el del seno.
Según el teorema del coseno:
d12 = a2 + d2 – 2ad cos α
Triángulo CDP
Este triángulo es rectángulo y con sus lados se construyen las razones trigonométricas del ángulo α:
sen α = h/d
cos α = PD/d
Pero el lado PD = a – b, por lo tanto:
cos α = (a-b) / d → a – b = d cos α
a = b + d cos α
También se tiene:
tg α = sen α / cos α = h / (a-b) → h = tg α (a-b)
Triángulo CDB
En este triángulo tenemos el ángulo cuyo vértice está en C. No está marcado en la figura, pero al comienzo se destacó que vale 180 – α. Este triángulo no es rectángulo, por lo que puede aplicarse teorema del coseno o teorema del seno.
Ahora bien, se puede demostrar fácilmente que:
sen (180 – α) = sen α
cos (180 – α) = – cos α
Aplicando el teorema del coseno:
d22 = d2 + b2 – 2db cos (180 – α) = d2 + b2 + 2db cos α
Los trapecios y en particular los trapecios rectángulos se encuentran en muchos lados, y a veces no siempre en forma tangible. Aquí tenemos varios ejemplos:
Las figuras geométricas abundan en la arquitectura de numerosas edificaciones, como esta iglesia en Nueva York, que muestra una estructura en forma de trapecio rectángulo.
Asimismo la forma trapezoidal es frecuente en el diseño de envases, contenedores, cuchillas (cutter o exacto), chapas y en diseño gráfico.

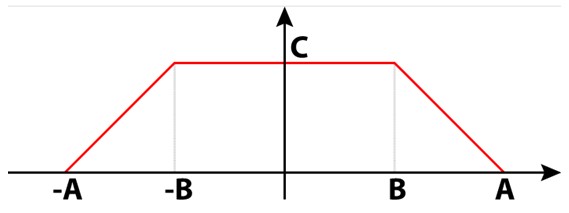
Las señales eléctricas no solamente pueden ser cuadradas, senoidales o triangulares. Existen también las señales trapezoidales que son de utilidad en numerosos circuitos. En la figura 4 hay una señal trapezoidal compuesta de dos trapecios rectángulos. Entre ambos forman un solo trapecio isósceles.
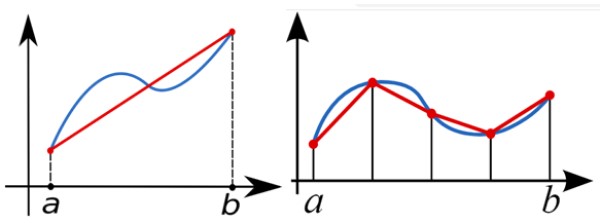
Para calcular en forma numérica la integral definida de la función f(x) entre a y b, se utiliza la regla del trapecio para aproximar el área bajo la gráfica de f(x). En la siguiente figura, a la izquierda la integral se aproxima con un solo trapecio rectángulo.
Una mejor aproximación es la de la figura derecha, con múltiples trapecios rectángulos.
Las fuerzas no siempre se concentran sobre un único punto, pues los cuerpos sobre los cuales actúan tienen dimensiones apreciables. Tal es el caso de un puente por el que circulan continuamente los vehículos, el agua de una piscina sobre las paredes verticales de la misma o un tejado sobre el que acumula agua o nieve.
Por eso las fuerzas se distribuyen por unidad de longitud, de superficie o de volumen, según el cuerpo sobre el cual actúan.
En el caso de una viga, una fuerza distribuida por unidad de longitud puede tener diversas distribuciones, por ejemplo la de trapecio rectángulo mostrada a continuación:
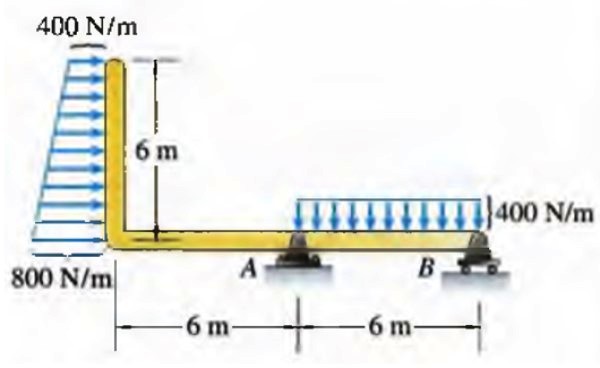
En la realidad, no siempre las distribuciones se corresponden a formas geométricas regulares como esta, pero sí pueden ser una buena aproximación en muchos casos.
Los bloques y láminas con formas geométricas, entre las que se incluyen los trapecios, son muy útiles para que los niños se familiaricen desde temprana edad con el fascinante mundo de la geometría.

En el trapecio rectángulo de la figura 1, la base mayor vale 50 cm y la base menor es igual a 30 cm, también se sabe que el lado oblicuo mide 35 cm. Encontrar:
a) Ángulo α
b) Altura
c) Perímetro
d) Base media
e) Área
f) Diagonales
Solución a
Los datos del enunciado se resumen de esta forma:
a = base mayor = 50 cm
b = base menor = 30 cm
d = lado inclinado = 35 cm
Para encontrar el ángulo α visitamos la sección de fórmulas y ecuaciones, para ver cuál es la que mejor se adapta a los datos ofrecidos. El ángulo buscado se encuentra en varios de los triángulos analizados, por ejemplo el CDP.
Allí tenemos esta fórmula, que contiene la incógnita y también los datos que conocemos:
cos α = (a-b) / d
Por lo tanto:
α = arcos [(a-b) / d] = arcos [(50-30) / 35 ] = arcos 20/35 = 55.15 º
Solución b
De la ecuación:
sen α = h/d
Se despeja h:
h = d.sen α = 35 sen 55.15 º cm = 28.72 cm
Solución c
El perímetro es la suma de los lados, y como la altura es igual al lado c, tenemos que:
c = h = 28.72 cm
Por lo tanto:
P = (50 + 30 + 35 + 28.72) cm = 143.72 cm
Solución d
La base media es la semisuma de las bases:
Base media = (50 + 30 cm )/2 = 40 cm
Solución e
El área del trapecio es:
A = base media x altura = 40 cm x 28.72 = 1148.8 cm2.
Solución f
Para la diagonal d1 se puede usar esta fórmula:
d12 = b2 + b2 = 2b2
d12= 2 x (30 cm)2 = 1800 cm2
d1 = √1800 cm2 = 42.42 cm
Y para la diagonal d2:
d22 = d2 + b2 + 2db cos α = (35 cm)2 + (30 cm)2 + 2 x 35 x 30 cm2 cos 55.15 º = 3325 cm2
d2 = √ 3325 cm2 = 57.66 cm
Esta no es la única manera de encontrar d2, ya que también está el triángulo DAB.
La siguiente gráfica de la velocidad en función del tiempo pertenece a un móvil que tiene movimiento rectilíneo uniformemente acelerado. Calcular la distancia recorrida por el móvil durante el intervalo de tiempo comprendido entre 0.5 y 1.2 segundos.
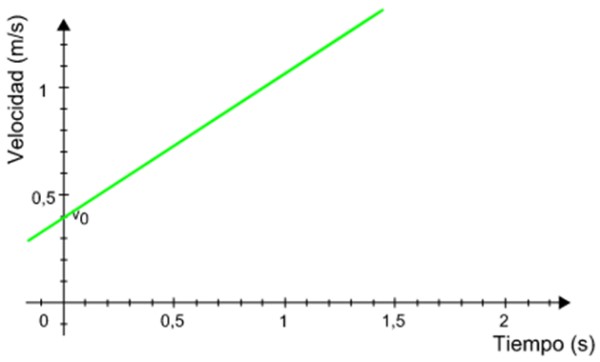
Solución
La distancia recorrida por el móvil equivale numéricamente al área bajo la gráfica, delimitada por el intervalo de tiempo indicado.
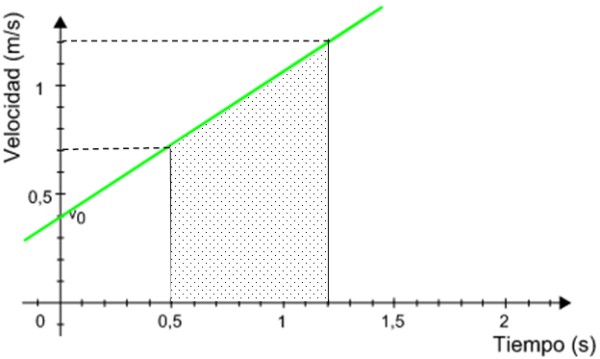
El área sombreada es el área de un trapecio rectángulo, dada por:
A =(Base mayor + base menor) x altura /2
A = (1.2 + 0.7) m/s x (1.2 – 0.5) s/2 = 0.665 m
- Baldor, A. 2004. Geometría plana y del espacio con trigonometría. Publicaciones Cultural.
- Bedford, A. 1996. Estática. Addison Wesley Interamericana.
- Jr. geometry. 2014. Polygons. Lulu Press, Inc.
- OnlineMSchool. Trapecio rectángulo. Recuperado de: es.onlinemschool.com.
- Solucionador automático de problemas de geometría. El trapecio. Recuperado de: scuolaelettrica.it
- Wikipedia. Trapecio (geometría). Recuperado de: es.wikipedia.org.
