Vectores no coplanares: definición, condiciones, ejercicios
Los vectores no coplanares son aquellos que no comparten el mismo plano. Dos vectores libres y un punto definen un único plano. Un tercer vector puede o no compartir ese plano y si no lo hace, se trata de vectores no coplanares.
Los vectores no coplanares no pueden representarse en espacios de dos dimensiones como una pizarra o una hoja de papel, porque alguno de ellos está contenido en la tercera dimensión. Para representarlos adecuadamente hay que usar perspectiva.
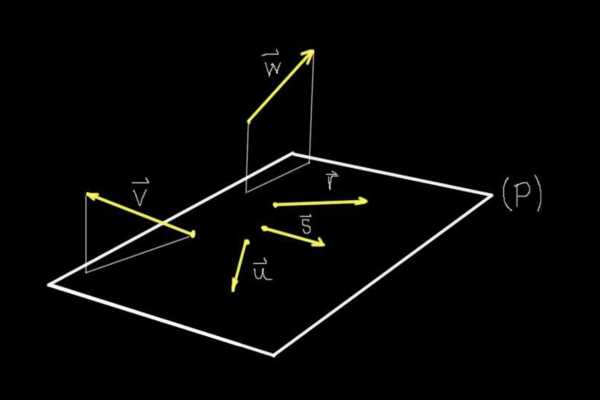
Si observamos la figura 1, todos los objetos mostrados estrictamente están en el plano de la pantalla, sin embargo gracias a la perspectiva nuestro cerebro es capaz de imaginar un plano (P) que sale de la misma.
Sobre ese plano (P) están los vectores r, s, u, mientras que los vectores v y w no están en ese plano.
Por lo tanto los vectores r, s, u son coplanarios o coplanares entre sí puesto que comparten el mismo plano (P). Los vectores v y w no comparten plano con alguno de los otros vectores mostrados, por lo tanto son no-coplanares.
Índice del artículo
- 1 Vectores coplanares y ecuación del plano
- 2 Condiciones para que tres vectores sean no coplanares
- 3 Ejercicios resueltos
- 4 Referencias
Un plano está definido de forma única si se dan tres puntos en el espacio tridimensional.
Supongamos que esos tres puntos son el punto A, el punto B y el punto C que definen el plano (P). Con estos puntos es posible construir dos vectores AB = u y AC = v que son por construcción coplanarios con el plano (P).
El producto vectorial (o producto cruz) de esos dos vectores da como resultado un tercer vector perpendicular (o normal) a ellos dos y por lo tanto perpendicular al plano (P):
n = u X v =>n ⊥ u y n ⊥ v =>n ⊥ (P)
Cualquier otro punto que pertenezca al plano (P) debe cumplir que el vector AQ sea perpendicular al vector n; esto es equivalente a decir que el producto escalar ( o producto punto) de n con AQ debe ser cero:
n • AQ = 0 (*)
La condición anterior es equivalente a decir que:
AQ • (u X v) = 0
Esta ecuación asegura que el punto Q pertenezca al plano (P).
La ecuación anterior puede escribirse en forma cartesiana. Para ello escribimos las coordenadas de los puntos A, Q y las componentes del vector normal n:
A=(a, b, c)
Q=(x, y, z)
n=(nx, ny, nz)
De modo que las componentes de AQ son:
AQ= ( x-a, y-b, z-c )
La condición para que el vector AQ esté contenido en el plano (P) es la condición (*) que ahora se escribe así:
(nx, ny, nz) • ( x-a, y-b, z-c ) = 0
Calculando el producto punto queda:
nx (x-a) + ny (y-b) + nz (z-b) = 0
Si se desarrolla y se reordena queda:
nx x + ny y + nz z = nx a + ny b + nz c
La expresión anterior es la ecuación cartesiana de un plano (P), en función de las componentes de un vector normal a (P) y las coordenadas de un punto A que pertenece a (P).
Como se ha visto en la sección previa la condición AQ • (u X v) = 0 garantiza que el vector AQ es coplanario a u y v.
Si denominamos w al vector AQ entonces podemos afirmar que:
w, u y v son coplanares, si y sólo si w • ( u X v ) = 0.
Si el producto triple (o producto mixto) de tres vectores es diferente de cero entonces esos tres vectores son no-coplanares.
Si w • ( u X v ) ≠ 0 entonces los vectores u, v, y w son no-coplanarios.
Si se introducen las componentes cartesianas de los vectores u, v, y w la condición de no-coplanaridad se puede escribir así:
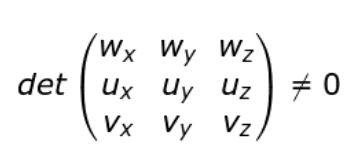
El producto triple tiene una interpretación geométrica y representa el volumen del paralelepípedo generado por los tres vectores no coplanares.
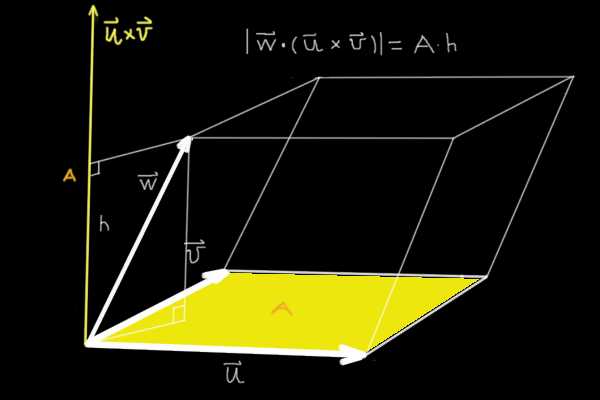
La razón es la siguiente; cuando se multiplica vectorialmente dos de los vectores no-coplanares se obtiene un vector cuya magnitud es el área del paralelogramo que ellos generan.
Luego cuando este vector se multiplica escalarmente por el tercer vector no coplanar, lo que se tiene es la proyección a un vector perpendicular al plano que determinan los dos primeros multiplicada por el área que ellos determinan.
Es decir se tiene el área del paralelogramo generado por los dos primeros multiplicada por la altura del tercer vector.
Si se tienen tres vectores y cualquiera de ellos no se puede escribir como combinación lineal de los otros dos, entonces los tres vectores son no-coplanares. Es decir tres vectores u, v y w son no-coplanares si la condición:
α u + β v + γ w = 0
Se cumple únicamente cuando α=0, β=0 y γ=0.
Se tienen tres vectores
u = ( -3, -6, 2); v = (4, 1, 0) y w = (-1, 2, z)
Note que la componente z del vector w es desconocida.
Encuentre el intervalo de valores que puede tomar z de modo tal que se garantice que los tres vectores no comparten el mismo plano.
Solución
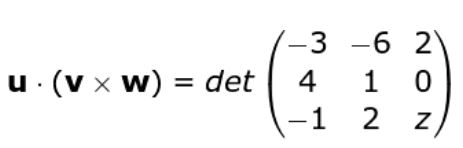
w • ( u X v )= -3(z – 0) + 6( 4 z – 0) + 2(8 + 1) = -3z + 24z + 18 = 21z + 18
Igualamos esta expresión al valor cero
21 z + 18 = 0
y despejamos z
z= -18/21= -6/7
Si la variable z tomase el valor -6/7 entonces los tres vectores serían coplanares.
De modo que los valores de z que garantizan que los vectores son no-coplanares son los que estén en el siguiente intervalo:
z ∈ (-∞,-6/7) U (-6/7, ∞)
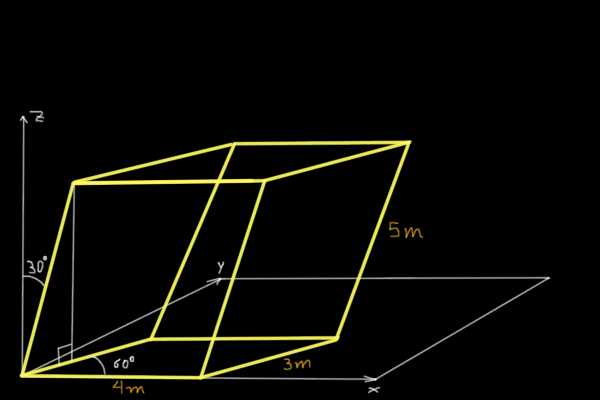
Encuentre el volumen del paralelepípedo mostrado en la siguiente figura:
Solución
Para encontrar el volumen del paralelepípedo mostrado en la figura, se determinarán las componentes cartesianas de tres vectores no-coplanares concurrentes en el origen del sistema de coordenadas. El primero de ellos es el vector u de 4m y paralelo al eje X:
u= (4, 0, 0) m
El segundo es el vector v en el plano XY de tamaño 3m que forma 60º con el eje X:
v= (3*cos 60º, 3*sen 60º, 0)= (1.5, 2.6, 0.0) m
Y el tercero el vector w de 5m y cuya proyección en el plano XY forma 60º con el eje X, además w forma 30º con el eje Z.
w= ( 5*sen 30º * cos 60º, 5*sen 30º * sen 60º, 5*sen 30º )
Efectuado los cálculos nos queda: w= ( 1.25, 2.17, 2.5) m.
- Figueroa, D. Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. 31-68.
- Física. Módulo 8: Vectores. Recobrado de: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mecánica para Ingenieros. Estática. 6ta Edición. Compañía Editorial Continental.28-66.
- McLean, W. Serie Schaum. Mecánica para Ingenieros: Estática y Dinámica. 3ra Edición. McGraw Hill. 1-15.
- Wikipedia. Vector. Recobrado de: es.wikipedia.org
