Regla de Simpson: fórmula, demostración , ejemplos, ejercicios
La regla de Simpson es un método para calcular, en forma aproximada, las integrales definidas. Se fundamenta en dividir el intervalo de integración en un número par de sub-intervalos igualmente espaciados.
Los valores extremos de dos sub-intervalos consecutivos definen tres puntos, por los que se ajusta una parábola, cuya ecuación es un polinomio de segundo grado.
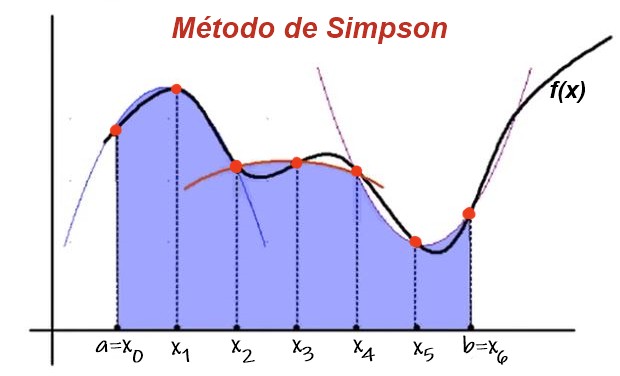
Luego el área bajo la curva de la función en los dos intervalos consecutivos se aproxima por el área del polinomio de interpolación. Sumando la contribución al área bajo la parábola de todos los sub-intervalos sucesivos, se tiene el valor aproximado de la integral.
Por otra parte, como la integral de una parábola puede calcularse algebraicamente en forma exacta, entonces es posible encontrar una fórmula analítica para el valor aproximado de la integral definida. Es conocida como la fórmula de Simpson.
El error del resultado aproximado así obtenido disminuye en la medida que el número de subdivisiones n sea mayor (siendo n un número par).
Más abajo se dará una expresión que permite estimar la cota superior del error de la aproximación a la integral I, cuando se ha hecho una partición de n subintervalos regulares del intervalo total [a, b].
Índice del artículo
El intervalo de integración [a, b] se subdivide en n subintervalos con n siendo un entero par. El ancho de cada subdivisión será:
h = (b – a)/n
De esta manera, sobre el intervalo [a, b] se hace la partición:
{X0, X1, X2, …, Xn-1, Xn}
Siendo X0 = a, X1 = X0 + h, X2 = X0 + 2h, …, Xn-1 = X0 + (n-1)h, Xn =X0 + nh = b.
La fórmula que permite calcular en forma aproximada la integral definida I de la función continua, y preferiblemente suave, en el intervalo [a, b] es:

Para obtener la fórmula de Simpson, en cada subintervalo [Xi, Xi+2] se aproxima la función f(X) por un polinomio p(X) de segundo grado (parábola) que pasa por los tres puntos: [Xi, f(Xi)]; [Xi+1, f(Xi+1)] y [Xi+2, f(Xi+2)].
Luego se calcula la integral del polinomio p(x) en [Xi, Xi+2] que aproxima a la integral de la función f(X) en ese intervalo.
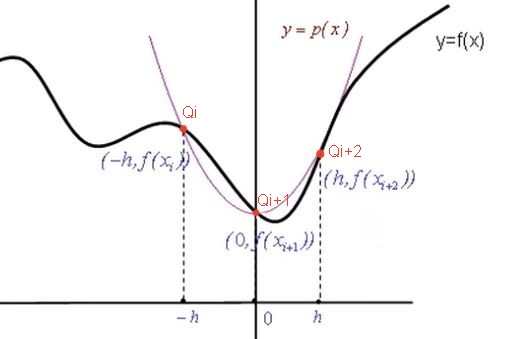
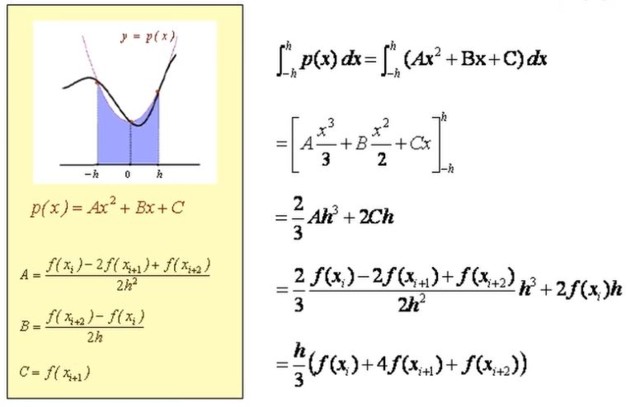
La ecuación de la parábola p(X) tiene la forma general: p(X) = A X2 + B X + C. Como la parábola pasa por los puntos Q señalados en rojo (ver figura), entonces los coeficientes A, B, C se determinan a partir del siguiente sistema de ecuaciones:
A (-h)2 – B h + C = f(Xi)
C = f(Xi+1)
A (h)2 + B h + C = f(Xi+2)
Puede observarse que el coeficiente C está determinado. Para determinar el coeficiente A sumamos la primera y la tercera ecuación obteniendo:
2 A h2 + 2 C = f(Xi) + f(Xi+2).
Luego se sustituye el valor de C y se despeja A quedando:
A = [f(Xi) – 2 f(Xi+1)+ f(Xi+2)] / (2 h2)
Para determinar el coeficiente B se resta la tercera ecuación de la primera y se despeja B obteniéndose:
B = [f(Xi+2) – f(Xi)] = 2 h.
En resumen, el polinomio de segundo grado p(X) que pasa por los puntos Qi, Qi+1 y Qi+2 tiene coeficientes:
A = [f(Xi) – 2 f(Xi+1)+ f(Xi+2)] / (2 h2)
B = [f(Xi+2) – f(Xi)] = 2 h
C = f(Xi+1)
Como ya se ha dicho, sobre el intervalo total de integración [a, b] se hace una partición {X0, X1, X2, …, Xn-1, Xn} con paso h = Xi+1 – Xi = (b – a)/ n, donde n es un número par.
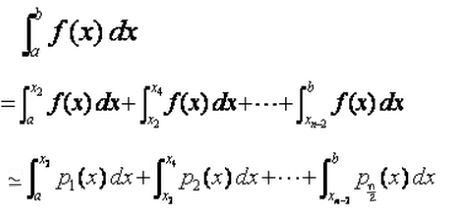
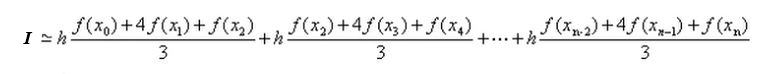

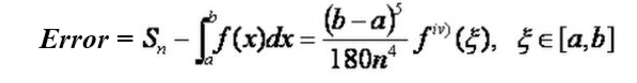
Nótese que el error disminuye con la cuarta potencia del número de subdivisiones del intervalo. Por ejemplo si se pasa de n subdivisiones a 2n, entonces el error disminuye en un factor 1/16.
La cota superior del error obtenido mediante la aproximación de Simpson puede obtenerse de esta misma fórmula, sustituyendo la derivada cuarta por el máximo valor absoluto de la derivada cuarta en el intervalo [a, b].
Considere la función la función f(X) = 1 / (1 + X2).
Encontrar la integral definida de la función f(X) en el intervalo [-1, 1] usando el método de Simpson con dos subdivisiones (n=2).
Solución
Se toma n = 2. Los límites de integración son a= -1 y b= -2, entonces la partición queda así:
X0= -1; X1= 0 y X2= +1.
Por lo tanto, la fórmula de Simpson adopta la siguiente forma:
Con n=2 → xo=-1, x1=0; x2=1, por lo tanto:
Considere la función f(X) = 1 / (1 + X2).
Encontrar la integral definida de la función f(X) en el intervalo [-1, 1] mediante la fórmula de Simpson con cuatro subdivisiones (n=4).
Solución
Se toma n = 4. Los límites de integración son a= -1 y b= -2, entonces la partición queda así:
X0= -1; X1= -1/2; X2= 0 ; X3= 1/2 y X4= +1.
La fórmula de Simpson se establece así:
Integral ≃ [(b -a)/(3 n)] [ f(X0) + 4 I + 2 P + f(Xn)]
Para el caso en el que se está aplicando, queda de la siguiente forma:
Integral ≃ {(1 – (1))/(3⋅4)] [ f(-1) + 4[f(-½) + f(½) ] + 2[f(0)] + f(1)}
Integral ≃ (2/12) [½ + 4 ( ⅘ + ⅘ ) + 2⋅1 + ½] = (⅙)[47/5] = 47/30 = 1,5666
Determine la integral definida de los ejemplos anteriores en forma exacta y hacer una comparación del resultado exacto con los obtenidos mediante la fórmula de Simpson en los ejemplos 1a y 1b.
Solución
La integral indefinida de la función f(X) = 1 / (1 + X2) es la función arctan(X).
Al evaluar en los límites de integración queda:
Integral = arctan(1) – arctan(-1) = π/4 – (-π/4) = π/2 = 1,5708
Si comparamos el resultado de la solución exacta con el obtenido por el método de Simpson con n=2 y n=4 tenemos:
Para n =2 la diferencia entre la solución exacta y la aproximada es π/2 – 5/3 = -0,0959, es decir una diferencia porcentual de -0,06%.
Y para la aproximación de Simpson con n=4, la diferencia entre la solución exacta y la aproximada es π/2 – 47/30 = 0,0041, es decir una diferencia porcentual de 0,003%.
El método de Simpson es adecuado para ser aplicado en lenguajes de programación y en aplicaciones informáticas destinadas a cálculos matemáticos. Se propone al lector que, basándose en las fórmulas dadas en este artículo, escriba su propio código en su programa favorito.
En la figura siguiente se muestra un ejercicio en el que se ha implementado la fórmula de Simpson en Smath Studio, un software gratuito disponible para los sistemas operativos Windows y Android.

- Casteleiro, J. M. 2002. Cálculo integral (Edición ilustrada). Madrid: ESIC Editorial.
- UPV. Método de Simpson. Universidad Politécnica de Valencia. Recuperado de: youtube.com
- Purcell, E. 2007. Cálculo Novena edición. Prentice Hall.
- Wikipedia. Regla de Simpson. Recuperado de: es.wikipedia.com
- Wikipedia. Interpolación polinómica de Lagrange. Recuperado de: es.wikipedia.com
