Álgebra de bloques: elementos, ejemplos, ejercicios resueltos

El álgebra de bloques se refiere al conjunto de operaciones que se ejecutan a través de bloques. Estos y algunos elementos más, sirven para representar esquemáticamente un sistema y visualizar fácilmente su respuesta ante una entrada determinada.

Por lo general un sistema contiene diversos elementos eléctricos, electrónicos y electromecánicos, y cada uno de ellos, con su respectiva función y posición en el sistema, así como la forma en que se relacionan, se esquematiza a través de bloques funcionales.

En la figura de arriba hay un sistema muy sencillo, que consta de una señal de entrada X(s), que entra al bloque con la función de transferencia G(s) que la modifica y produce la salida Y(s).

Es conveniente representar las señales y su recorrido por el sistema mediante flechas que entran y salen de cada bloque. Usualmente el flujo de señales se dirige de izquierda a derecha.

La ventaja de esta clase de esquema es la ayuda visual que presta para comprender el sistema, aunque no constituya una representación física del mismo. De hecho, el diagrama de bloques no es único, porque según el punto de vista pueden dibujarse incluso varios diagramas de un mismo sistema.

También puede ocurrir que un mismo diagrama sirva para varios sistemas que no necesariamente están relacionados entre sí, siempre que describa adecuadamente su comportamiento. Existen sistemas diferentes cuya respuesta es semejante en muchos aspectos, por ejemplo un circuito LC (inductor-capacitor) y un sistema masa-resorte.

Índice del artículo

• 1 ¿Qué es un diagrama de bloques?
• 2 Elementos del diagrama de bloques
  • 2.1 La señal
  • 2.2 El bloque
  • 2.3 Punto de suma
  • 2.4 Punto de ramificación
• 3 Ejemplos de reglas del álgebra de bloques
  • 3.1 Bloques en cascada
  • 3.2 Bloques en paralelo
  • 3.3 Mover un sumador a la izquierda
  • 3.4 Mover un sumador a la derecha
  • 3.5 Mover un punto de bifurcación de izquierda a derecha
  • 3.6 Mover un punto de bifurcación de derecha a izquierda
  • 3.7 Sistema con retroalimentación
  • 3.8 Sistema con retroalimentación y transductor
• 4 Ejercicios resueltos
  • 4.1 Ejercicio 1
  • 4.2 Ejercicio 2
• 5 Referencias

¿Qué es un diagrama de bloques?

Los sistemas por lo general son más complicados que el de la figura 1, pero el álgebra de bloques provee una serie de reglas simples para manipular el esquema del sistema y reducirlo a su versión más sencilla.

Tal como se explicó al comienzo, el diagrama se vale de bloques, flechas y círculos para establecer la relación entre cada componente del sistema y el flujo de las señales que lo recorren.

El álgebra de bloques permite comparar dos o más señales mediante suma, resta y multiplicación de las mismas, así como analizar la contribución que cada componente hace al sistema.

Gracias a esto es posible reducir todo el sistema a una sola señal de entrada, una función de transferencia única que describe completamente la acción del sistema y la correspondiente salida.

Elementos del diagrama de bloques

Los elementos del diagrama de bloques son los siguientes:

La señal

Las señales son de naturaleza muy variada, por ejemplo es común que sea una corriente eléctrica o un voltaje, pero puede ser luminosa, sonora y más. Lo importante es que contiene información acerca de un determinado sistema.

La señal se denota con una letra mayúscula si es función de la variable s de la transformada de Laplace: X(s) (ver figura 1) o con minúscula si está en función del tiempo t, como x(t).

En el diagrama de bloques, la señal de entrada se representa mediante una flecha dirigida hacia el bloque, mientras que la señal de salida, denotada como Y(s) o y (t), se indica con una flecha saliente.

Tanto la señal de entrada como la de salida son únicas y la dirección en que fluye la información está determinada por el sentido de la flecha. Y el álgebra es la misma para cualquiera de las dos variables.

El bloque

El bloque se representa mediante un cuadrado o un rectángulo (ver figura 1) y se puede usar para llevar a cabo operaciones o implementar la función de transferencia, que se denota por lo general con la letra mayúscula G. Dicha función es un modelo matemático mediante el cual se describe la respuesta que ofrece el sistema ante una señal de entrada.

La función de transferencia puede expresarse en términos del tiempo t como G (t) o de la variable s como G(s).

Al llegar la señal de entrada X(s) al bloque se multiplica por la función de transferencia y se transforma en la señal de salida Y(s). Matemáticamente se expresa así:

Y(s) = X(s).G(s)

Equivalentemente, la función de transferencia es la razón entre la transformada de Laplace de la señal de salida y la transformada de Laplace de la señal de entrada, siempre que las condiciones iniciales del sistema sean nulas:

G(s) = Y(s) / X(s)

Punto de suma

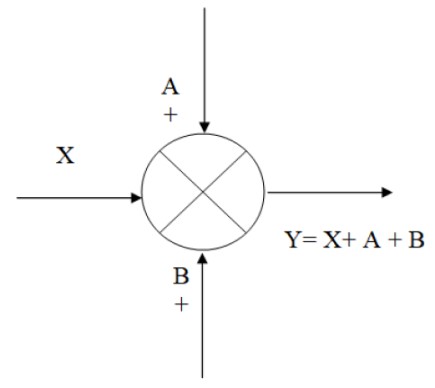
El punto de suma o sumador, se simboliza mediante un círculo con una cruz dentro. Se utiliza para combinar, mediante sumas y restas, dos o más señales. En el extremo de la flecha que simboliza la señal se coloca directamente un signo + si dicha señal se suma o un signo – si se resta.

En la siguiente figura hay un ejemplo de cómo funciona el sumador: se tiene la señal de entrada X, a la cual se le suman las señales A y B, obteniendo como resultado la salida Y, que algebraicamente equivale a:

Y = X+A+B

Punto de ramificación

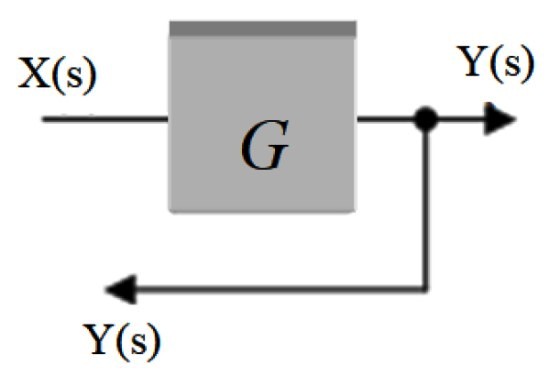
También se llama punto de bifurcación. En él la señal que sale de un bloque se distribuye hacia otros bloques o bien hacia un sumador. Se representa mediante un punto colocado sobre la flecha de la señal y de él sale otra flecha que redirige la señal hacia otra parte.

Ejemplos de reglas del álgebra de bloques

Como se explicó antes, la idea es expresar el sistema mediante el diagrama de bloques y reducirlo para encontrar la función de transferencia que lo describe. Las siguientes son las reglas del álgebra de bloques para simplificar los diagramas:

Bloques en cascada

Cuando se tiene una señal que atraviesa sucesivamente por los bloques G₁, G₂, G₃…, se reduce a un bloque único cuya función de transferencia es el producto de G₁, G₂, G₃…

En el siguiente ejemplo, la señal X(s) entra al primer bloque y su salida es:

Y₁(s) = X(s).G₁(s)

A su vez Y₁(s) entra al bloque G₂(s), cuya salida es:

Y₂(s) = X(s).G₁(s). G₂(s)

El procedimiento es válido para n bloques en cascada:

Y_n (s) = X(s). G₁(s).G₂(s)…..G_n(s)

Bloques en paralelo

En el diagrama de la izquierda, la señal X(s) se bifurca para entrar a los bloques G₁(s) y G₂(s):

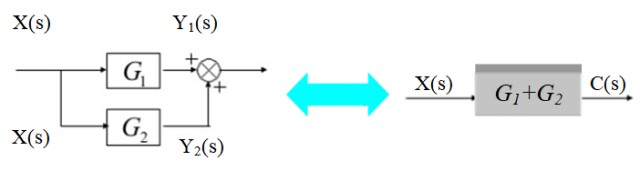
Las respectivas señales de salida son:

Y₁(s) = X(s).G₁(s)

Y₂(s) = X(s).G₂(s)

Estas señales se suman para obtener:

C(s) = Y₁(s) + Y₂(s) = X(s).[G₁(s) + G₂(s)]

Como se muestra en el diagrama de la derecha.

Mover un sumador a la izquierda

Un sumador se puede desplazar a la izquierda del bloque del siguiente modo:

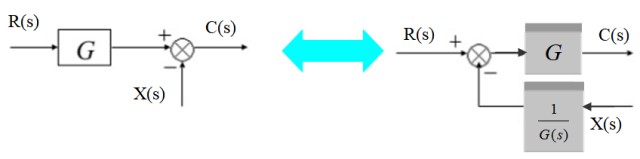
A la izquierda la señal de salida es:

C(s)=R(s). G(s) – X(s)

Equivalentemente a la derecha:

C(s)=[R(s) – X(s)/G(s)].G(s)

Mover un sumador a la derecha

El sumador se puede mover a la derecha del bloque así:

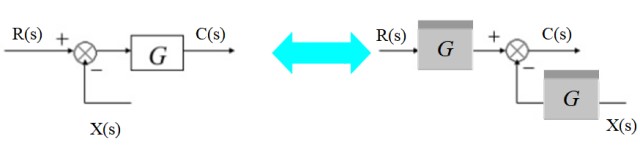
A la izquierda se tiene: [R(s) – X(s)].G(s) = C(s)

Y a la derecha:

R(s). G(s) – X(s).G(s) = C(s)

Mover un punto de bifurcación de izquierda a derecha

Para desplazar el punto de bifurcación de izquierda a derecha del bloque, basta con observar que la salida C(s)  a la derecha es el producto X(s).G(s). Como se quiere convertirlo en X(s) nuevamente, se multiplica por el inverso de G(s).

Mover un punto de bifurcación de derecha a izquierda

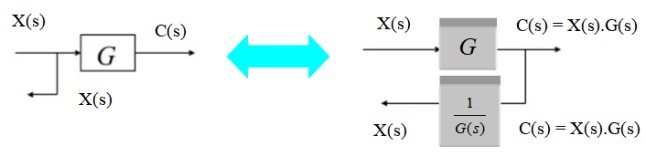
Alternativamente el punto de bifurcación se puede desplazar de derecha a izquierda como sigue:

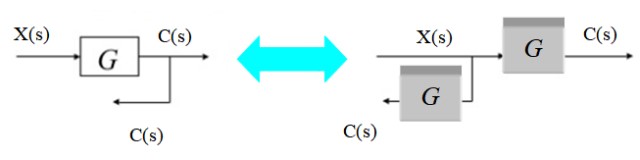
Ya que a la salida de la bifurcación se quiere obtener C(s), simplemente se intercala un nuevo bloque G(s) en un punto de bifurcación a la izquierda del bloque original.

Sistema con retroalimentación

En el siguiente sistema la señal de salida C(s) se retroalimenta a través del sumador a la izquierda:

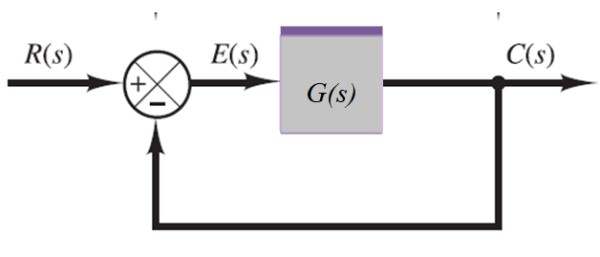
C(s) = E(s).G(s)

Pero:

E(s) = R(s) –C(s)

Sustituyendo esta expresión en la ecuación  anterior queda: C(s) = [R(s) –C(s)].G(s), de la que puede despejarse C(s):

C(s) + C(s).G(s) = R(s).G(s) → C(s). [1 + G(s)] = R(s).G(s)

C(s) = R(s).G(s) / [1 + G(s)]

O alternativamente:

C(s) / R(s) = G(s) / [1 + G(s)]

En forma gráfica, luego de simplificar queda:

Sistema con retroalimentación y transductor

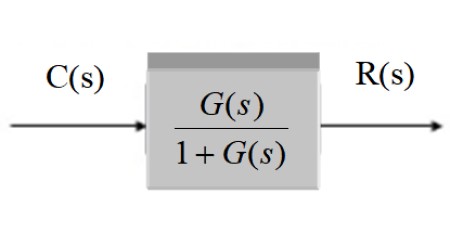
El transductor consiste en la función de transferencia H(s):

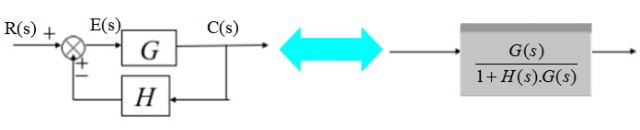
En el diagrama de la derecha, la señal de salida C(s) es:

C(s) = E(s). G(s) con E(s) = R(s) – C(s).H(s)

Entonces:

C(s) = [R(s) – C(s). H(s)]. G(s)

C(s) [1+ H(s).G(s)] = R(s).G(s)

Por lo tanto, C(s) se puede despejar mediante:

C(s)  = G(s).R(s) / [1+ H(s).G(s)]

Y la función de transferencia será:

G(s) / [1+ H(s).G(s)]

Como se muestra en el diagrama simplificado de la derecha.

Ejercicios resueltos

Ejercicio 1

Encontrar la función de transferencia del siguiente sistema:

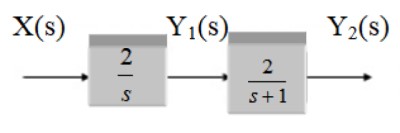
Solución

Se trata dos bloques en cascada, por lo tanto la función de transferencia es el producto de las funciones G₁ y G₂.

Se tiene que:

G₁ = 2/s

G₂ =  2 /(s+1)

Por lo tanto la función de transferencia buscada es:

G(s) = 4 / [s (s+1)]

Ejercicio 2

Reducir el siguiente sistema:

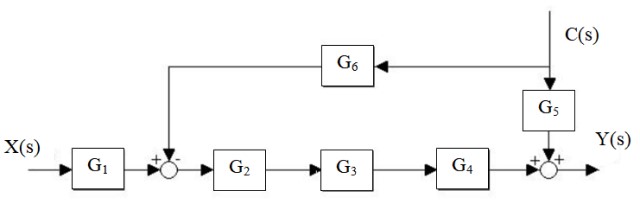
Solución

En primer lugar se reduce la cascada G₂, G₃ y G_4, y se separa el paralelo G₅ y G₆:

Después, el sumador a la izquierda del bloque G₂ ⋅G₃ ⋅ G₄ se traslada a la derecha:

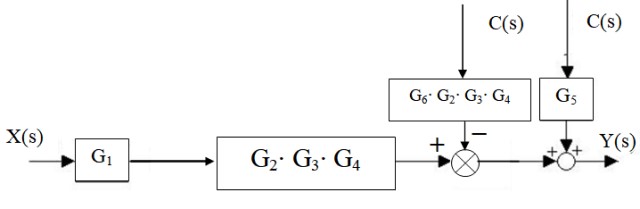
Los sumadores de la derecha se reducen a uno solo, así como los bloques en cascada:

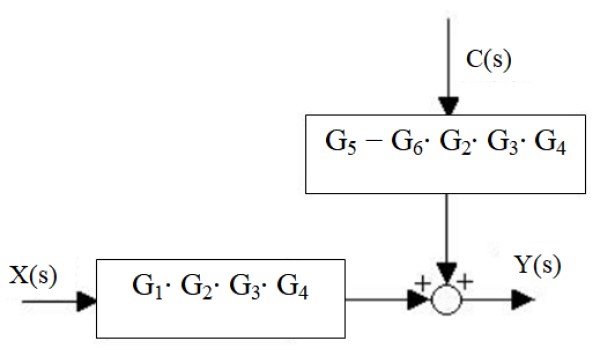
Finalmente, la salida del sistema es:

Y (s) = X(s)⋅G₁⋅ G₂ ⋅G₃ ⋅ G₄ + C(s)⋅[G₅ – G₆ ⋅ G₂ ⋅G₃ ⋅ G₄]

Referencias

1. Alaydi, J. Control system block diagram. Recuperado de: site.iugaza.edu.ps.
2. Bolton, W. 2006. Ingeniería de control. 2da. Edición. Alfaomega.
3. Cwalinsky, J. Introduction to system block algebra. Recuperado de: cedengineering.com.
4. Dademuchconnection. Diagrama de bloques. Recuperado de: dademuch.com.
5. Ogata, K. 2010. Ingeniería de control moderna. 5ta. Edición. Pearson.