Función homográfica: cómo graficar, ejercicios resueltos
La función homográfica o racional es un tipo de función matemática compuesta por la división de dos componentes polinómicas. Obedece a la forma P(x)/Q(x), donde Q(x) no puede tomar forma nula.

Por ejemplo la expresión (2x – 1)/(x + 3) corresponde a una función homográfica con P(x) = 2x – 1 y Q(x) = x + 3.
Las funciones homográficas constituyen una sección de estudio de las funciones analíticas, siendo tratadas desde el enfoque de graficación y desde el estudio del dominio y rango. Esto es debido a las restricciones y fundamentos que deben aplicarse para sus resoluciones.
Índice del artículo
- 1 ¿En qué consiste una función homográfica?
- 2 Función homográfica mixta
- 3 ¿Cómo graficar una función homográfica?
- 4 Ejemplos
- 5 Ejercicio 2
- 6 Referencias
Son expresiones racionales de variable única, aunque esto no quiere decir que no exista una expresión similar para dos o más variables, donde ya se estaría en presencia de cuerpos en el espacio que obedecen a los mismo patrones que la función homográfica en el plano.
Poseen raíces reales en algunos casos, pero siempre se mantiene la existencia de asíntotas verticales y horizontales, así como de también intervalos de crecimiento y decrecimiento. Comúnmente solo una de estas tendencias se hace presente, pero existen expresiones capaces de mostrar ambas en su desarrollo.
Su dominio está restringido por las raíces del denominador, debido a que no existe la división entre cero de los números reales.
Son muy frecuentes en el cálculo, sobretodo diferencial e integral, siendo necesario derivar y antiderivar bajo fórmulas particulares. Se clasifican a continuación algunas de las más comunes.
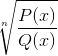
Excluye todos los elementos del dominio que hacen negativo al argumento. Las raíces presentes en cada polinomio arrojan valores de cero al ser evaluadas.
Estos valores son aceptados por el radical, aunque se debe considerar la restricción fundamental de la función homográfica. Donde Q(x) no puede recibir valores nulos.
Se deben interceptar las soluciones de los intervalos:
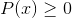
Para conseguir la solución de las intersecciones se puede recurrir al método de signos, entre otros.
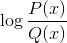
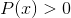
También es común encontrar ambas expresiones en una sola, entre otras combinaciones posibles.
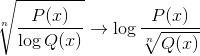
Las funciones homográficas se corresponden gráficamente con hipérbolas en el plano. Las cuales se transportan horizontal y verticalmente según los valores que definen a los polinomios.
Existen varios elementos que debemos definir para graficar una función racional u homográfica.
El primero serán las raíces o ceros de las funciones P y Q.

Los valores conseguidos se denotarán en el eje x de la gráfica. Indicando las intersecciones de la gráfica con el eje.
Corresponden a rectas verticales, que demarcan la gráfica según las tendencias que estas presenten. Tocan al eje x en los valores que hacen cero al denominador y nunca serán tocadas por la gráfica de la función homográfica.
Representada por una línea puntada horizontal, demarca un límite para el cual la función no estará definida en el punto exacto. Las tendencias se observarán antes y después de esta línea.
Para calcularla debemos recurrir a un método similar al método de L’Hopital, usado para resolver límites de funciones racionales que tienden al infinito. Se deben tomar los coeficientes de las potencias más altas en el numerador y el denominador de la función.
Por ejemplo, la siguiente expresión tiene una asíntota horizontal en y = 2/1 = 2.

Los valores de las ordenadas tendrán tendencias marcadas en la gráfica debido a las asíntotas. En el caso del crecimiento, la función aumentará de valores según se evalúen los elementos del dominio de izquierda a derecha.
Los valores de las ordenadas disminuirán según se evalúen los elementos del dominio de izquierda a derecha.
Los saltos encontrados en los valores no se tomarán en cuenta como aumentos o disminuciones. Esto ocurre cuando la gráfica está próxima a una asíntota vertical u horizonta, donde los valores pueden variar del infinito al infinito negativo y viceversa.
Haciendo cero el valor de x, se encuentra la intersección con el eje de las ordenadas. Este es un dato muy útil para la obtención de la gráfica de la función racional.
Defina la gráfica de las siguientes expresiones, encuentre sus raíces, asíntotas vertical y horizontal, intervalos de crecimiento y decrecimiento e intersección con el eje de las ordenadas.
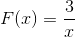
La expresión carece de raíces, debido a que posee un valor constante en el numerador. La restricción a aplicar será x diferente de cero. Con asíntota horizontal en y = 0, y asíntota vertical en x = 0. No existen puntos de intersección con el eje y.
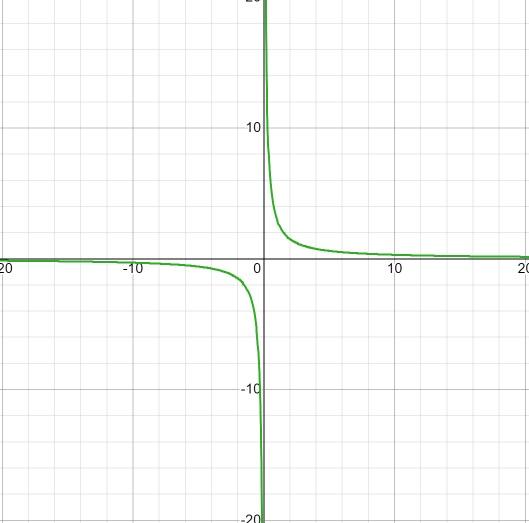
Se observa que no existen intervalos de crecimiento incluso con el salto de menos a más infinito que hay en x = 0.
El intervalo de decrecimiento es
ID: (-∞ ; o) U (0 , ∞)
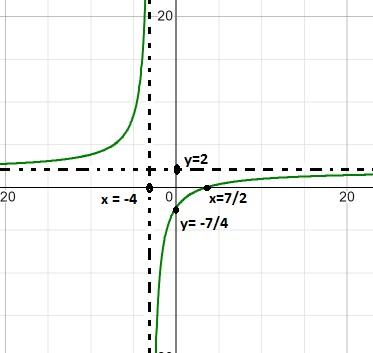
Se observan 2 polinomios como en la definición inicial, por eso se procede según los pasos establecidos.
La raíz encontrada es x = 7/2 que resulta de igualar a cero la función.
La asíntota vertical está en x = – 4, que es el valor excluido del dominio por la condición de función racional.
La asíntota horizontal está en y = 2, esto después de dividir 2/1, los coeficientes de las variables de grado 1.
Posee una intersección con las ordenadas en y = – 7/4. Valor encontrado después de igualar la x a cero.
La función crece constantemente, con un salto de más a menos infinito alrededor de la raíz x = -4.
Su intervalo de crecimientos es ( -∞ , – 4) U (- 4 , ∞).
Cuando el valor de x se acerca a menos infinito, la función toma valores cercanos a 2. Lo mismo sucede cuando la x se aproxima a más infinito.
La expresión se aproxima a más infinito cuando se evalúa en – 4 por la izquierda, y a menos infinito cuando se evalúa en – 4 por la derecha.
Se observa la gráfica de la siguiente función homográfica:
Describir su comportamiento, raíces, asíntotas vertical y horizontal, intervalos de crecimiento y decrecimiento e intersección con el eje de las ordenadas.
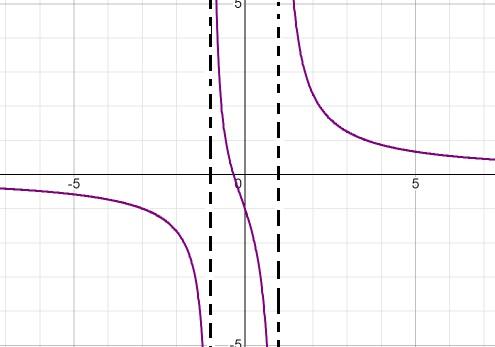
El denominador de la expresión nos indica al factorizar la diferencia de cuadrados (x + 1) (x – 1) los valores de las raíces. De esta forma se pueden definir ambas asíntotas verticales como:
x = -1 y x = 1
La asíntota horizontal corresponde al eje de las abscisas debido a que la potencia mayor se encuentra en el denominador.
Su única raíz está definida por x = -1/3.
La expresión siempre decrece de izquierda a derecha. Se aproxima a cero cuando se tiende a los infinitos. A menos infinito al aproximarse a -1 por la izquierda. A más infinito al aproximarse a -1 por la derecha. Menos infinito al aproximarse a 1 por la izquierda y más infinito al aproximarse a 1 por la derecha.
- Approximation with Rational Functions. Donald J. Newman. American Mathematical Soc., 31 dic. 1979
- Orthogonal Rational Functions. UNIVERSIDAD DE LA LAGUNA TENERIFE ADHEMAR BULTHEEL, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav Njastad. Cambridge University Press, 13 feb. 1999
- Rational Approximation of Real Functions. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 mar. 2011
- Algebraic Functions. Gilbert Ames Bliss. Courier Corporation, 1 ene. 2004
- Revista de la Sociedad matematica espanola, Volúmenes 5-6. Sociedad matematica espanola, Madrid 1916
