Antecedentes históricos de la geometría analítica
Los antecedentes históricos de la geometría analítica se remontan al siglo XVII, cuando Pierre de Fermat y René Descartes definieron su idea fundamental. Su invención seguía la modernización del álgebra y de la notación algebraica de François Viète.
Este campo tiene sus bases en la Antigua Grecia, especialmente en los trabajos de Apolonio y Euclides, quienes tuvieron una gran influencia en este área de las matemáticas.
La idea esencial detrás de la geometría analítica es que una relación entre dos variables, de manera que una es una función de la otra, define una curva. Esta idea fue desarrollada por primera vez por Pierre de Fermat. Gracias a este marco esencial, Isaac Newton y Gottfried Leibniz pudieron desarrollar el cálculo.
El filósofo francés Descartes también descubrió un acercamiento algebraico a la geometría, aparentemente por su cuenta. El trabajo de Descartes sobre la geometría aparece en su famoso libro Discurso del método.
En este libro se señala que el compás y las construcciones geométricas de bordes rectos involucran la suma, la resta, la multiplicación y las raíces cuadradas.
La geometría analítica representa la unión de dos importantes tradiciones en las matemáticas: la geometría como el estudio de la forma, y la aritmética y álgebra, que tienen que ver con la cantidad o los números. Por lo tanto, la geometría analítica es el estudio del campo de la geometría utilizando sistemas de coordenadas.
Historia
Antecedentes de la geometría analítica
La relación entre la geometría y el álgebra ha evolucionado a lo largo de la historia de las matemáticas, aunque la geometría alcanzó un grado de madurez más temprano.

Por ejemplo, el matemático griego Euclides fue capaz de organizar muchos resultados en su libro clásico Los elementos.
Pero fue el antiguo griego Apolonio de Perga quien pronosticó el desarrollo de la geometría analítica en su libro Cónicas. Él definió una cónica como la intersección entre un cono y un plano.
Utilizando los resultados de Euclides en triángulos similares y secantes de círculos, encontró una relación dada por las distancias de cualquier punto “P” de una cónica a dos líneas perpendiculares, el eje mayor de una cónica y la tangente en un punto final del eje. Apolonio utilizó esta relación para deducir propiedades fundamentales de las cónicas.
El desarrollo subsecuente de sistemas de coordenadas en matemáticas emergió solo después de que el álgebra había madurado gracias a los matemáticos islámicos e indios.
Hasta el Renacimiento la geometría era utilizada para justificar las soluciones para problemas algebraicos, pero no existía mucho que el álgebra pudiera aportar a la geometría.
Esta situación cambiaría con la adopción de una notación conveniente para las relaciones algebraicas y el desarrollo del concepto de una función matemática, que ahora era posible.
Siglo XVI
Al final del siglo XVI el matemático francés François Viète introdujo la primera notación algebraica sistemática, utilizando letras para representar cantidades numéricas, tanto conocidas como desconocidas.
También desarrolló poderosos métodos generales para trabajar expresiones algebraicas y resolver ecuaciones algebraicas.

Gracias a esto, los matemáticos no eran completamente dependientes de las figuras geométricas y de la intuición geométrica para resolver problemas.
Incluso algunos matemáticos comenzaron a abandonar la manera geométrica estándar de pensar, según la cual las variables lineales de longitudes y cuadrados corresponden a áreas, mientras que los cúbicos corresponden a los volúmenes.
Los primeros en tomar este paso fueron el filósofo y matemático René Descartes, y el abogado y matemático Pierre de Fermat.
Fundación de la geometría analítica
Descartes y Fermat fundaron independientemente la geometría analítica durante la década de 1630, al adoptar el álgebra de Viète para el estudio del lugar geométrico.
Estos matemáticos se dieron cuenta de que el álgebra era una herramienta de gran poder en la geometría e inventaron lo que hoy en día se conoce como geometría analítica.
Un avance que lograron fue superar a Viète al usar letras para representar distancias que son variables en vez de fijas.
Descartes utilizó ecuaciones para estudiar las curvas definidas geométricamente, y resaltó la necesidad de considerar las curvas generales algebraicas-gráficas de ecuaciones polinómicas en los grados “x” e “y”.

Por su lado, Fermat enfatizó que cualquier relación entre las coordinadas “x” e “y” determina una curva.
Utilizando estas ideas, reestructuró las declaraciones de Apolonio sobre los términos algebraicos y restauró algunos de sus trabajos que se encontraban perdidos.
Fermat indicó que cualquier ecuación cuadrática en “x” e “y” puede ser colocada en la forma estándar de una de las secciones cónicas. A pesar de esto, Fermat nunca publicó sus trabajos realizados sobre el tema.
Gracias a sus avances, lo que Arquímedes solo podía resolver con gran dificultad y para casos aislados, Fermat y Descartes lo podían resolver rápidamente y para una gran cantidad de curvas (conocidas ahora como curvas algebraicas).
Pero sus ideas solo ganaron la aceptación general a través de los esfuerzos de otros matemáticos en la última mitad del siglo XVII.
Los matemáticos Frans van Schooten, Florimond de Beaune y Johan de Witt ayudaron a expandir el trabajo de Decartes y añadieron material adicional importante.
Influencia
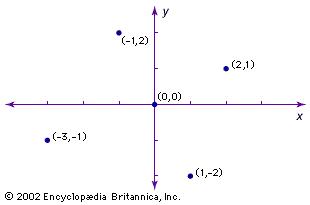
En Inglaterra John Wallis popularizó la geometría analítica. Utilizó ecuaciones para definir las cónicas y derivar sus propiedades. Aunque usaba coordenadas negativas libremente, fue Isaac Newton quien utilizó dos ejes oblicuos para dividir el plano en cuatro cuadrantes.
Newton y el alemán Gottfried Leibniz revolucionaron las matemáticas al final del siglo XVII al demostrar independientemente el poder del cálculo.
Newton demostró la importancia de los métodos analíticos en la geometría y su papel en el cálculo, cuando aseveró que cualquier cubo (o cualquier curva algebraica de tercer grado) tiene tres o cuatro ecuaciones estándares para ejes de coordenadas adecuados. Con ayuda del mismo Newton, el matemático escocés John Stirling lo probó en 1717.
Geometría analítica de tres y más dimensiones
Aunque tanto Descartes como Fermat sugirieron utilizar tres coordenadas para estudiar las curvas y superficies en el espacio, la geometría analítica tridimensional se desarrolló lentamente hasta 1730.

Los matemáticos Euler, Hermann y Clairaut produjeron ecuaciones generales para cilindros, conos y superficies de revolución.
Por ejemplo, Euler utilizó ecuaciones para traslaciones en el espacio para transformar la superficie cuadrática general, de manera que sus ejes principales coincidieran con sus ejes de coordenada.
Euler, Joseph-Louis Lagrange y Gaspard Monge hicieron que la geometría analítica se independizara de la geometría sintética (no analítica).
Referencias
- The development of analytic geometry (2001). Recuperado de encyclopedia.com
- History of analytic geometry (2015). Recuperado de maa.org
- Analysis (Mathematics). Recuperado de britannica.com
- Analytic geometry. Recuperado de britannica.com
- Descartes and the birth of analytic geometry. Recuperado de sciencedirect.com
