Prueba de Tukey: en qué consiste, caso de ejemplo, ejercicio resuelto
La prueba de Tukey es un método que tiene como fin comparar las medias individuales provenientes de un análisis de varianza de varias muestras sometidas a tratamientos distintos.
El test, presentado en el año 1949 por John.W. Tukey, permite discernir si los resultados obtenidos son significativamente diferentes o no. Se le conoce también como la prueba de diferencia honestamente significativa de Tukey (Tukey’s HSD test por sus siglas en inglés).
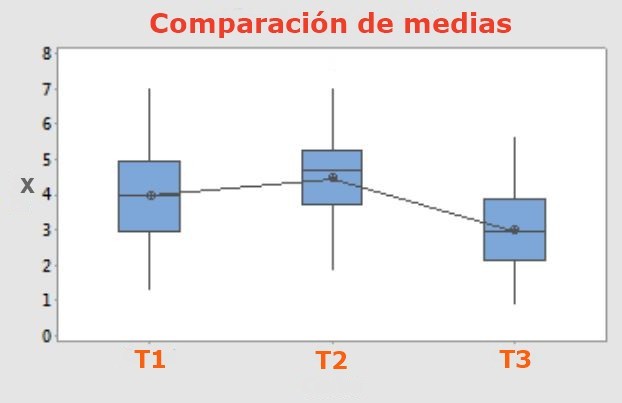
En los experimentos donde se compara entre tres o más tratamientos diferentes aplicados a igual número de muestras, se requiere discernir si los resultados son significativamente distintos o no.
Se dice que un experimento es balanceado cuando el tamaño de todas las muestras estadísticas es igual en cada tratamiento. Cuando el tamaño de las muestras es diferente para cada tratamiento, se tiene entonces un experimento no balanceado.
En ocasiones no es suficiente con un análisis de varianza (ANOVA) para saber si en la comparativa de diferentes tratamientos (o experimentos) aplicada a varias muestras cumplen la hipótesis nula (Ho: “todos los tratamientos son iguales”) o por el contrario se cumple la hipótesis alternativa (Ha: “por lo menos uno de los tratamientos es diferente”).
La prueba de Tukey no es única, existiendo muchas más pruebas para comparar medias muestrales, pero esta es una de la más conocidas y aplicadas.
Índice del artículo
En la aplicación de esta prueba se calcula un valor w llamado el comparador de Tukey cuya definición es como sigue:
w = q √(MSE /r)
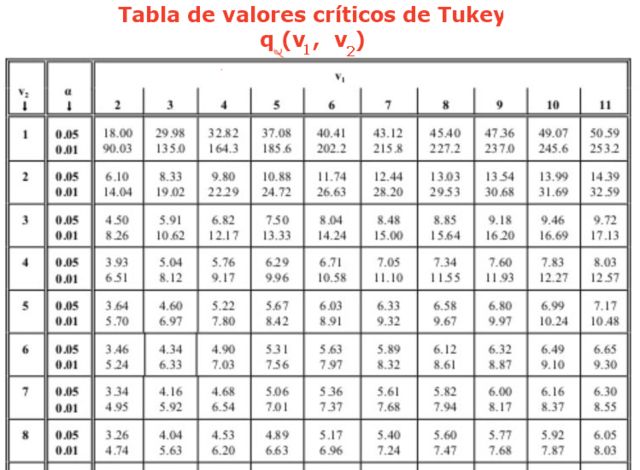
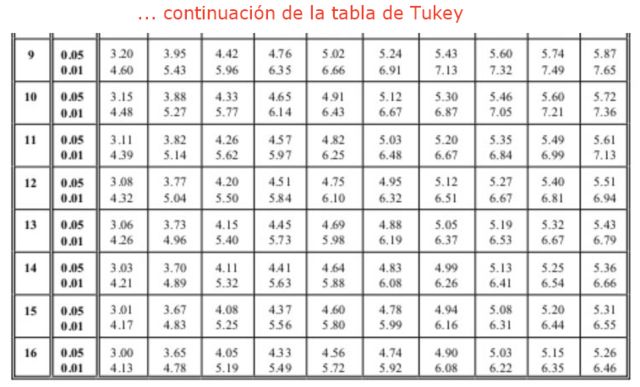
Donde el factor q se obtiene de una tabla (Tabla de Tukey), que consta de filas de valores q para diferente número de tratamientos o experimentos. Las columnas indican el valor de factor q para diferentes grados de libertad. Normalmente las tablas disponibles tienen significancias relativas de 0.05 y 0.01.
En esta fórmula, dentro de la raíz cuadrada aparece el factor MSE (Cuadrado Medio del Error) divido entre r, que indica el número de repeticiones. El MSE es un número que se obtiene normalmente a partir de un análisis de varianzas (ANOVA).
Cuando la diferencia entre dos valores medios sobrepasa al valor w (comparador de Tukey), entonces se concluye que se trata de promedios diferentes, pero si la diferencia es menor que el número de Tukey, entonces se trata de dos muestras con valor promedio estadísticamente idéntico.
Al número w se le conoce también como número HSD (Diferencia Honestamente Significativa).
Este único número comparador puede aplicarse si el número de las muestras aplicadas para la prueba de cada tratamiento es igual en cada uno de ellos.
Cuando por algún motivo el tamaño de las muestras es diferente en cada tratamiento a comparar, entonces el procedimiento descrito anteriormente difiere ligeramente y se conoce como prueba de Tukey-Kramer.
Ahora se obtiene un número w comparador para cada par de tratamientos i, j:
w(i,j) = q √( ½ MSE /(ri +rj) )
En esta fórmula, el factor q se obtiene de la tabla de Tukey. Dicho factor q depende del número de tratamientos y los grados de libertad del error. ri es el número de repeticiones en el tratamiento i, mientras que rj es el número de repeticiones en el tratamiento j.
Un criador de conejos desea hacer un estudio estadístico fiable que le indique saber cuál de las cuatro marcas de alimento de engorde de conejos es la más efectiva. Para el estudio forma cuatro grupos con seis conejos de mes y medio de edad que hasta ese momento tuvieron las mismas condiciones de alimentación.
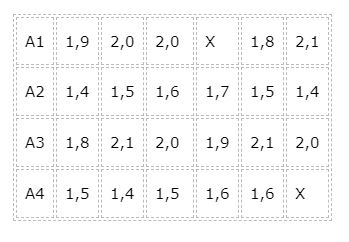
Las razones fueron que en los grupos A1 y A4 ocurrieron fallecimientos debido a causas no atribuibles a los alimentos, ya que uno de los conejos fue picado por un insecto y en el otro caso seguramente el fallecimiento fue causa de un defecto congénito. De modo que los grupos quedan desbalanceados y entonces es necesario aplicar la prueba de Tukey-Kramer.
Para no alargar demasiado los cálculos, se tomará como ejercicio resuelto un caso de experimento balanceado. Se tomará como datos los siguientes:
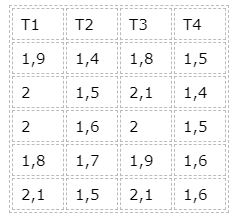
En este caso se tienen cuatro grupos correspondientes a cuatro tratamientos diferentes. Sin embargo, observamos que todos los grupos tienen el mismo número de datos, por lo que se trata entonces de un caso balanceado.
Para realizar el análisis ANOVA se ha usado la herramienta que viene incorporada en la hoja de cálculo de Libreoffice. Otras hojas de cálculo como Excel tienen incorporada esta herramienta para el análisis de datos. A continuación se muestra una tabla resumen que ha resultado después de haberse realizado el análisis de varianza (ANOVA):
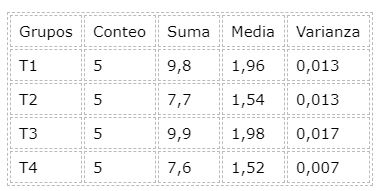
Del análisis de varianza también se tiene el valor P, que para el ejemplo es 2,24E-6 muy por debajo del 0.05 del nivel de significancia, lo que directamente conduce a rechazar la hipótesis nula: Todos los tratamientos son iguales.
Es decir, entre los tratamientos algunos tienen valores medios diferentes, pero hay que saber cuales son los significativa y honestamente distintos (HSD) desde el punto de vista estadístico usando la prueba de Tukey.
Para hallar el número w o como también se le conoce el número HSD requerimos hallar el cuadrado medio del error MSE. Del análisis ANOVA se obtiene que la suma de cuadrados dentro de los grupos es SS=0,2; y el número de grados de libertad dentro de los grupos es df=16 con estos datos podemos hallar MSE:
MSE = SS/df = 0,2/16 = 0,0125
También se requiere encontrar el factor q de Tukey, usando la tabla. Se busca en la columna 4 que corresponde a los 4 grupos o tratamientos a comparar y la fila 16, ya que el análisis ANOVA arrojó 16 grados de libertad dentro de los grupos. Esto nos conduce a un valor de q igual a: q = 4,33 correspondiente a 0,05 de significancia o 95% de confiabilidad. Finalmente se halla el valor para la “diferencia honestamente significativa”:
w = HSD = q √(MSE /r) = 4,33 √(0,0125 /5) = 0,2165
Para saber cuales son los grupos o tratamientos honestamente diferentes hay que conocer los valores promedios de cada tratamiento:

También es necesario conocer las diferencias entre los valores medios de pares de tratamientos, lo cual se muestra en la siguiente tabla:
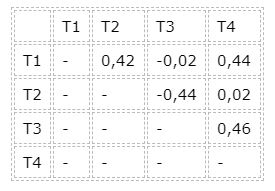
Se concluye que los mejores tratamientos, en cuanto a maximizar el resultado son el T1 o el T3, los cuales son indiferentes desde el punto de vista estadístico. Para elegir entre T1 y T3, habría que buscar otros factores ajenos al análisis presentado aquí. Por ejemplo, precio, disponibilidad, etc.
- Cochran William y Cox Gertrude. 1974. Diseños experimentales. Trillas. México. Tercera reimpresión. 661p.
- Snedecor, G.W. and Cochran, W.G. 1980. Statistical methods. Seventh Ed. Iowa, The Iowa State University Press. 507p.
- Steel, R.G.D. y Torrie, J.H. 1980. Principles and procedures of Statistics: A Biometrical Approach (2nd Ed.). McGraw-Hill, New York. 629p.
- Tukey, J. W. 1949. Comparing individual means in the analysis of variance. Biometrics, 5:99-114.
- Wikipedia. Tukey’s test. Recuperado de: en.wikipedia.com
