Vectores en el espacio: cómo graficar, aplicaciones, ejercicios
Un vector en el espacio es todo aquel representado mediante un sistema de coordenadas dado por x, y y z. Casi siempre el plano xy es el plano de la superficie horizontal y el eje z representa la altura (o profundidad).
Los ejes coordenados cartesianos mostrados en la figura 1, dividen al espacio en 8 regiones denominadas octantes, análogo a como los ejes x – y dividen al plano en 4 cuadrantes. Tendremos entonces 1er octante, 2do octante y así sucesivamente.
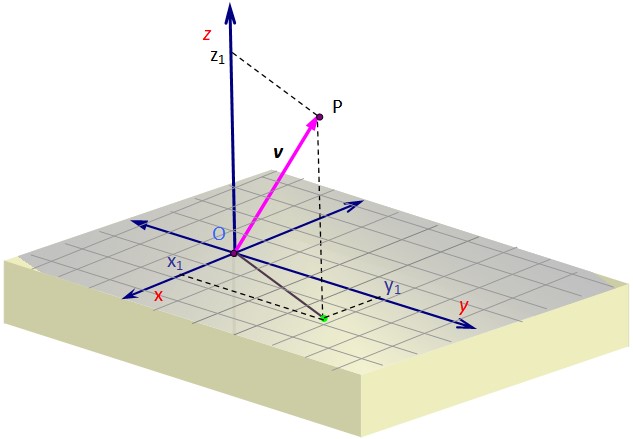
La figura 1 contiene una representación de un vector v en el espacio. Se requiere algo de perspectiva para crear la ilusión de tres dimensiones sobre el plano de la pantalla, que se logra dibujando una vista oblicua.
Para graficar un vector 3D hay que ayudarse de las líneas punteadas que determinan sobre la cuadrícula las coordenadas de la proyección o “sombra” de v sobre la superficie x-y. Dicha proyección comienza en O y termina en el punto verde.
Una vez allí hay que seguir por la vertical hasta la altura (o profundidad) necesaria según el valor de z, hasta llegar a P. El vector se dibuja partiendo de O y terminando en P, que en el ejemplo está en el 1er octante.
Índice del artículo
Los vectores en el espacio son extensamente utilizados en mecánica y otras ramas de la física y la ingeniería, ya que las estructuras que nos rodean requieren de la geometría en las tres dimensiones.
Los vectores de posición en el espacio se usan para posicionar objetos con respecto a un punto de referencia llamado origen O. Por ello también son herramientas necesarias en la navegación, pero eso no es todo.
Las fuerzas que actúan sobre estructuras como pernos, soportes, cables, puntales y más son de naturaleza vectorial y están orientadas en el espacio. Con la finalidad de conocer su efecto, es necesario saber su dirección (y también su punto de aplicación).
Y frecuentemente la dirección de una fuerza se tiene conociendo dos puntos en el espacio que pertenezcan a su línea de acción. De esta forma la fuerza es:
F = F u
Donde F es la magnitud o módulo de la fuerza y u es el vector unitario (de módulo 1) dirigido a lo largo de la línea de acción de F.
Antes de pasar a resolver algunos ejemplos, se repasará brevemente la notación de vectores en 3D.
En el ejemplo de la figura 1, el vector v, cuyo punto de origen coincide con el origen O y cuyo final es el punto P, tiene coordenadas x y z positivas, mientras que la coordenada y es negativa. Estas coordenadas son: x1, y1, z1, las cuales son precisamente las coordenadas de P.
De manera que si tenemos un vector ligado al origen, es decir, cuyo punto de inicio coincide con O, es muy sencillo indicar sus coordenadas, las cuales serán las del punto extremo o P. Para distinguir entre un punto y un vector, utilizaremos para los últimos letras negritas y corchetes, así:
v = x1, y1, z1 >
Mientras que el punto P se denota con paréntesis:
P = (x1, y1, z1)
Otra representación hace uso de los vectores unitarios i, j y k que definen las tres direcciones del espacio en los ejes x, y y z respectivamente.
Estos vectores son perpendiculares entre sí y conforman una base ortonormal (ver figura 2). Esto significa que un vector en 3D puede escribirse en términos de ellos como:
v = vxi + vyj + vz k
En la figura 2 se muestran además los ángulos directores γ1, γ2 y γ3 que el vector v hace respectivamente con los ejes x, y y z. Conociendo estos ángulos y la magnitud del vector, este queda completamente determinado. Además, los cosenos de los ángulos directores cumplen la siguiente relación:
(cos γ1)2 + (cos γ2)2 + (cos γ3)2 = 1

En la figura 2 los ángulos γ1, γ2 y γ3 que el vector v de módulo 50 forma con los ejes coordenados son respectivamente: 75.0º, 60.0º y 34.3º. Encuentre las componentes cartesianas de este vector y represéntelo en términos de los vectores unitarios i, j y k.
Solución
La proyección del vector v sobre el eje x es vx = 50 . cos 75º = 12.941. De igual manera la proyección de v sobre el eje y es vy = 50 cos 60 º = 25 y finalmente sobre el eje z es vz = 50. cos 34.3º = 41.3. Ahora v puede expresarse como:
v = 12.9 i + 25.0 j + 41.3 k
Encontrar las tensiones en cada uno de los cables que sujetan al balde de la figura que está en equilibrio, si el peso de este es de 30 N.

Solución
Sobre el balde, el diagrama de cuerpo libre indica que TD (verde) compensa al peso W (amarillo), por lo tanto TD = W = 30 N.
En el nudo, el vector TD está dirigido verticalmente hacia abajo, luego:
TD = 30 (-k) N.
Para establecer las tensiones restantes hay que seguir los siguientes pasos:
Paso 1: Hallar las coordenadas de todos los puntos
A = (4.5; 0; 3) (A está sobre el plano de la pared x-z)
B = (1.5; 0; 0) (B está sobre el eje x)
C = (0, 2.5, 3) (C está sobre el plano de la pared y-z)
D = (1.5; 1.5; 0) (D está sobre el plano horizontal x-y)
Paso 2: Hallar los vectores en cada dirección restando las coordenadas del final y del inicio
DA = 3; -1.5; 3>
DC = -1.5; 1; 3>
DB = 0; -1.5 ; 0>
Paso 3: Calcular módulos y vectores unitarios
Un vector unitario se obtiene mediante la expresión: u = r / r, con r (en negrita) siendo el vector y r (sin negrita) el módulo de dicho vector.
DA = (32 + (-1.5)2 + 32)½ = 4.5 ; DC = ((-1.5) 2 + 12 + 32)½ = 3.5
uDA = 3; -1.5; 3>4.5 = 0.67 ; -0.33 ; 0.67>
uDC = -1.5; 1; 3>3.5 = -0.43; 0.29; 0.86>
uDB = 0; -1; 0>
uD = 0; 0; -1>
Paso 4: Expresar todas las tensiones como vectores
TDA = TDA uDA = TDA0.67 ; -0.33 ; 0.67>
TDC = TDC uDC = TDC -0.43; 0.29; 0.86>
TDB = TDB uDB =TDB 0; -1; 0>
TD = 30 0; 0; -1>
Paso 5: Aplicar la condición de equilibrio estático y resolver el sistema de ecuaciones
Finalmente se aplica la condición de equilibrio estático al balde, de manera que la suma vectorial de todas las fuerzas sobre el nudo sea nula:
TDA + TDC + TDB + TD = 0
Como las tensiones están en el espacio, dará lugar a un sistema de tres ecuaciones para cada componente (x, y y z) de las tensiones.
0.67 TDA -0.43 TDC + 0 TDB = 0
-0.33 TDA + 0.29 TDC – TDB = 0
0.67 TDA + 0.86 TDC +0 TDB – 30 = 0
La solución es: TDA = 14.9 N; TDA = 23.3 N; TDB = 1.82 N
- Bedford, 2000. A. Mecánica para Ingeniería: Estática. Addison Wesley. 38-52.
- Figueroa, D. Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática.31-68.
- Física. Módulo 8: Vectores. Recobrado de: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mecánica para Ingenieros. Estática. 6ta Edición. Compañía Editorial Continental. 15-53.
- Vector Addition Calculator. Recobrado de: 1728.org
