Tercera ley de la termodinámica: fórmulas, ecuaciones, ejemplos
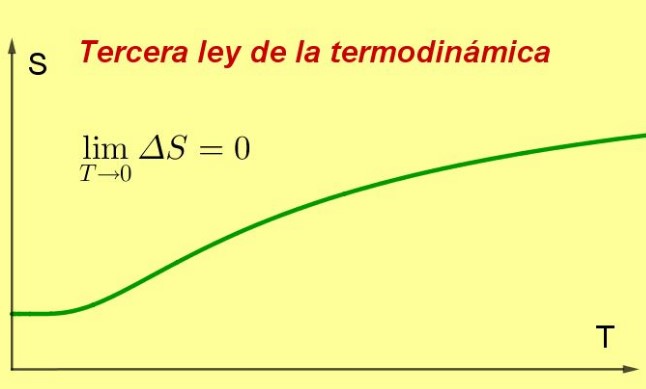
La tercera ley de la termodinámica establece que la entropía de un sistema termodinámico cerrado en equilibrio tiende a ser mínima y constante, a medida que su temperatura se acerca a 0 kelvin.
Dicho valor de la entropía será independiente de las variables del sistema (la presión o el campo magnético aplicado, entre otras). Lo que sucede es que a medida que la temperatura es más cercana a 0 K, los procesos en el sistema se van deteniendo y como la entropía es una medida de la agitación interna, forzosamente desciende.
Índice del artículo
- 1 Conceptos previos
- 2 Fórmulas y ecuaciones
- 3 Aplicaciones
- 4 Ejemplos
- 5 Ejercicios resueltos
- 6 Referencias
Para comprender el alcance de la tercera ley de la termodinámica, relevante a muy bajas temperaturas, es necesario revisar los siguientes conceptos:
Generalmente se refiere a un gas, a un líquido o a un sólido. Lo que no sea parte del sistema se denomina entorno. El sistema termodinámico más común es el gas ideal, que consta de N partículas (átomos) que sólo interactúan mediante colisiones elásticas.
A los sistemas aislados no se les permite intercambio alguno con el entorno. Los sistemas cerrados no intercambian materia con el entorno pero sí calor. Por último, los sistemas abiertos pueden intercambiar tanto materia como calor con el entorno.
El macroestado de un sistema es el conjunto de valores que tienen sus variables: presión, temperatura, volumen, número de moles, entropía y energía interna. En cambio, el microestado -en caso de un gas ideal-, viene dado por la posición y el momentum de cada una de las N partículas que lo conforman, en un determinado instante.
Muchos microestados pueden dar como resultado un mismo macroestado. En un gas a temperatura ambiente, el número de microestados posibles es inmenso, porque el número de partículas que lo conforman, las diferentes posiciones y la diferentes energías que pueden adoptar es muy grande.
La entropía como dijimos, es una variable macroscópica termodinámica que mide el grado de desorden molecular del sistema. El grado de desorden de un sistema es más grande en la medida que el número de microestados posibles es mayor.
Se necesita de este concepto para formular la tercera ley de la termodinámica en forma matemática. Sea S la entropía del sistema, entonces:
La entropía es una variable de estado macroscópica que se relaciona directamente con el número de microestados posibles de un sistema, mediante la siguiente fórmula:
S = k ln(W)
En la ecuación anterior: S representa la entropía, W el número de microestados posibles del sistema y k es la constante de Boltzmann (k =1.38 x 10-23 J/K). Es decir, la entropía de un sistema es k veces el logaritmo natural del número de microestados posibles.
Es posible definir la entropía absoluta de una sustancia pura partiendo de la definición de la variación de la entropía:
δQ = n . cp .dT
Aquí cp es el calor específico molar y n el número de moles. La dependencia del calor específico molar con la temperatura es un dato obtenido experimentalmente y conocido para muchas sustancias puras.
De acuerdo a la tercera ley en las sustancias puras:
En la vida diaria, la tercera ley de la termodinámica tiene pocas aplicaciones, muy al contrario de la primera y la segunda ley. Se debe a que es un principio que se refiere a lo que pasa en un sistema cuando se acerca al 0 absoluto, un rango de temperaturas poco frecuentes.
De hecho alcanzar el 0 absoluto o −273,15 °C es imposible (ver ejemplo 1 más adelante) Sin embargo, la tercera ley se aplica al estudiar la respuesta de los materiales a muy bajas temperaturas.
Gracias a esto han surgido importantes avances en Física de la materia condensada, tales como:
-Superfluidez (ver ejemplo 2 más adelante)
-Superconductividad
-Técnicas de enfriamiento por láser
-El condensado de Bose-Einstein
-Los gases superfluidos de Fermi.

A temperaturas extremadamente bajas, el descenso de la entropía permite el surgimiento de interesantes fenómenos cuánticos. Por eso, veamos lo que sucede con la entropía de un sistema a muy baja temperatura.
Cuando se tiene una sustancia cristalina perfecta, su entropía mínima es exactamente cero, ya que se trata de un sistema altamente ordenado. En temperaturas cercanas al 0 absoluto, la materia se encuentra en estado condensado (líquido o sólido) y las vibraciones en el cristal son mínimas.
Algunos autores consideran un enunciado alternativo de la tercera ley de la termodinámica el siguiente:
“Si la materia se condensa formando un cristal perfecto, cuando la temperatura tiende al cero absoluto, la entropía tiende exactamente a cero”.
Puntualicemos algunos aspectos del enunciado anterior:
– Un cristal perfecto es aquel en el que cada molécula es idéntica y en el que la estructura molecular se repite idénticamente en toda su extensión.
– A medida que la temperatura tiende al cero absoluto, la vibración atómica disminuye casi por completo.
Entonces el cristal conforma una sola configuración o microestado posible, es decir W=1, y por lo tanto la entropía es igual a cero:
S = k ln(1) = 0
Pero no siempre que un material enfriado cerca del cero absoluto forma un cristal, y mucho menos este cristal es perfecto. Esto ocurre únicamente si el proceso de enfriamiento es muy lento y reversible.
De lo contrario, factores como impurezas presentes en el cristal harían posible la existencia de otros microestados. Por lo tanto W > 1 y la entropía sería mayor que 0.
Si el proceso de enfriamiento es brusco, durante el mismo el sistema pasa por una sucesión de estados de no equilibrio, que conducen a que el material se vitrifique. En tal caso, no se produce estructura cristalina y ordenada, sino un sólido amorfo, cuya estructura es semejante a la de un líquido.
En ese caso, el valor mínimo de entropía en las cercanías del cero absoluto no es cero, ya que el número de microestados es bastante mayor que 1. La diferencia entre esta entropía y la entropía nula del estado cristalino perfecto se conoce como la entropía residual.
La explicación es que por debajo de cierta temperatura umbral, el sistema no tiene otra posibilidad más que ocupar los microestados de menor energía, que por estar cuantizados, constituyen un número fijo.
Ellos se encargarán de mantener la entropía constante, aun cuando la temperatura siga descendiendo hacia el cero absoluto.
El principio de indeterminación de Heisenberg establece que la incertidumbre en la posición y el momentum de una partícula, por ejemplo en los átomos de una red cristalina, no son independientes una de del otro, sino que siguen la siguiente desigualdad:
Δx ⋅ Δp ≥ h
Donde h es la constante de Planck. Es decir, la incertidumbre en la posición multiplicada por la incertidumbre en el momentum (masa por velocidad) es mayor o igual que la constante de Planck, cuyo valor es muy pequeño, pero no cero: h=6.63 x 10-34 J·s.
¿Y qué tiene que ver el principio de incertidumbre con la tercera ley de la termodinámica? Si la posición de los átomos de la red cristalina es fija y precisa (Δx=0) entonces la rapidez de estos átomos puede tomar cualquier valor entre 0 e infinito. Esto se contradice con el hecho que en el cero absoluto, todo movimiento de agitación térmica cesa.
Recíprocamente, si partimos que en el cero absoluto de temperatura, toda agitación cesa y el momentum de cada átomo de la red es exactamente cero (Δp=0), entonces el principio de incertidumbre de Heisenberg implicaría que la indeterminación en las posiciones de cada átomo sería infinita, es decir que pueden estar en cualquier posición.
Como consecuencia de la afirmación anterior, el número de microestados tendería al infinito y la entropía también tomaría un valor indeterminado.
En la superfluidez, que ocurre a muy bajas temperaturas, la materia pierde la fricción interna entre sus moléculas, denominada viscosidad. En tal caso, el fluido podría circular sin fricción por siempre, pero el problema es a esas temperaturas casi nada es líquido excepto el helio.
El helio y el helio 4 (su isótopo más abundante) constituyen un caso único, puesto que a presión atmosférica y a temperaturas cercanas al cero absoluto, el helio permanece líquido.
Cuando el helio-4 se somete a temperatura por debajo de 2.2 K a presión atmosférica se convierte en un superfluido. Este descubrimiento ocurrió en 1911 en Leyden por el físico holandés Heike Kamerlingh Onnes (1853-1926).
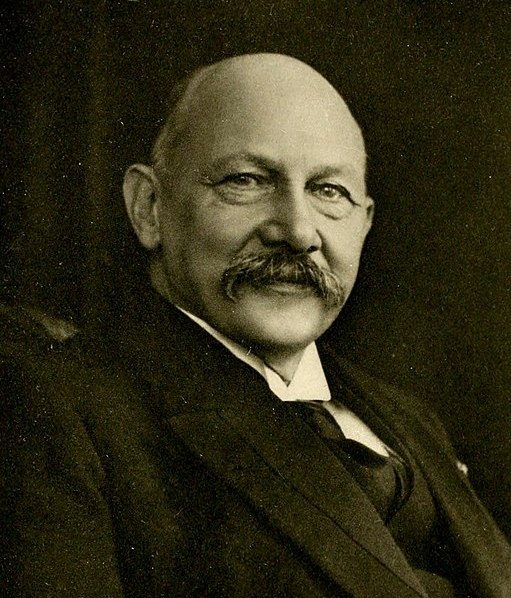
El átomo de helio-4 es un bosón. Los bosones, a diferencia de los fermiones, son partículas que pueden ocupar todas el mismo estado cuántico. Por lo tanto los bosones no cumplen el principio de exclusión de Pauli.
Entonces todos los átomos de helio-4 a temperaturas por debajo de 2.2 K ocupan el mismo estado cuántico y por lo tanto no hay más que un sólo microestado posible, implicando que el helio-4 superfluido tiene S= 0.
Consideremos un caso sencillo que consta de un sistema conformado sólo por tres partículas que disponen de tres niveles de energía. Para este sencillo sistema:
a) Determine el número de microestados posibles para tres rangos de temperatura:
-Alta
-Media
-Baja
b) Determine por medio de la ecuación de Boltzmann la entropía en los diferentes rangos de temperatura.
c) Discuta los resultados y explique si contradicen o no la tercera ley de la termodinámica.
Solución a
A escala molecular y atómica, las energías que puede adoptar un sistema están cuantizadas, lo que significa que únicamente pueden tomar ciertos valores discretos. Además, cuando las temperaturas son tan bajas, las partículas que conforman el sistema solo tienen la posibilidad de ocupar los niveles de menor energía.
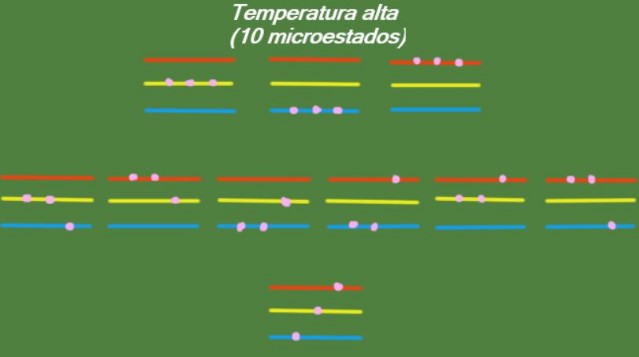
Temperatura alta
Si el sistema tiene una temperatura T relativamente alta, entonces las partículas tienen suficiente energía para ocupar cualquiera los niveles disponibles, dando lugar a 10 microestados posibles, los cuales aparecen en la siguiente figura:
Temperatura media
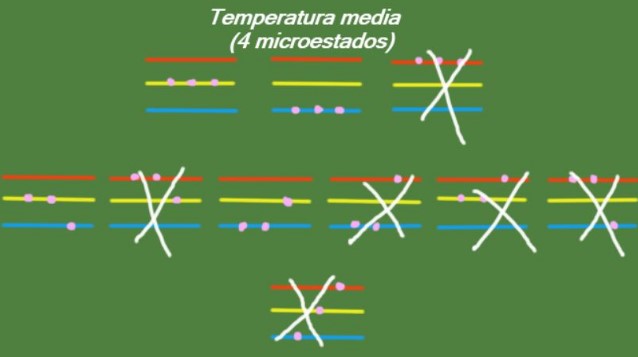
En el caso que el sistema posea una temperatura intermedia, entonces las partículas que lo conforman no tienen energía suficiente para ocupar el nivel más alto de energía. Los microestados posibles se ilustran en la figura:
Temperatura baja
Si la temperatura continúa descendiendo en nuestro sistema idealizado de tres partículas y tres niveles de energía, entonces las partículas dispondrán de tan poca energía que solo podrán ocupar el nivel más bajo. En este caso, queda solamente 1 microestado posible, tal como se aprecia en la figura 6:
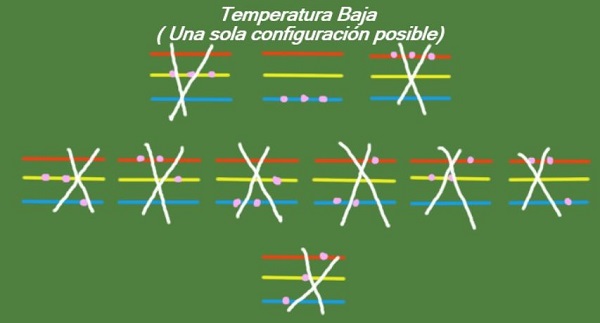
Solución b
Conocido ya el número de microestados en cada rango de temperatura, ya podemos utilizar la ecuación de Boltzmann dada anteriormente para hallar la entropía en cada caso.
S = k ln(10) = 2.30 x k = 3.18 x 10-23 J/K (Temperatura alta)
S = k ln(4) = 1.38 x k = 1.92 x 10-23 J/K (Temperatura media)
Y finalmente:
S = k ln(1) = 0 (Temperatura baja)
Solución c
En primer lugar notamos que la entropía decrece a medida que la temperatura desciende, tal como se esperaba. Pero para los valores más bajos de temperatura se llega a un valor umbral, a partir del cual se alcanza el estado base del sistema.
Aun cuando la temperatura sea tan cercana como sea posible al cero absoluto, no hay estados de menor energía disponibles. Entonces la entropía mantiene su valor mínimo constante, que en nuestro ejemplo es S=0.
Este ejercicio ilustra, a nivel de los microestados de un sistema, la razón por la que se cumple la tercera ley de la termodinámica.
Razone si el siguiente enunciado es verdadero o falso:
“La entropía de un sistema en el cero absoluto de temperatura es exactamente cero”.
Justifique la respuesta y describa algunos ejemplos.
Solución
La respuesta es: falso.
En primer lugar el 0 absoluto de temperatura no puede alcanzarse porque se violaría el principio de incertidumbre de Heisenberg y la tercera ley de la termodinámica.
Es muy importante observar que en la tercera ley no se dice lo que pasa en el 0 absoluto, sino cuando la temperatura es infinitamente cercana al 0 absoluto. La diferencia es sutil, pero significativa.
La tercera ley tampoco afirma que cuando la temperatura toma un valor arbitrariamente cercano al cero absoluto la entropía tiende a cero. Esto ocurriría únicamente en el caso analizado previamente: el cristal perfecto, que es una idealización.
Muchos sistemas a escala microscópica, es decir a escala cuántica, tienen su nivel base de energía degenerado, lo que significa la existencia de varias configuraciones en el nivel de energía más baja.
Lo anterior significa que en estos sistemas la entropía nunca sería exactamente cero. Tampoco la entropía sería exactamente cero en sistemas que se vitrifican cuando la temperatura tiende al cero absoluto. En tal caso, queda la entropía residual antes vista.
Se debe a que sus moléculas quedaron “atascadas” antes de llegar a ocupar los niveles más bajos de energía disponibles, lo cual aumenta considerablemente el número de microestados posibles, imposibilitando que la entropía sea exactamente cero.
- Cengel, Y. 2012. Termodinámica. 7ma Edición. McGraw Hill. 347.
- Jet Propulsion Laboratory. The Coolest Spot in the Universe. Recobrado de: coldatomlab.jpl.nasa.gov.
- González, A. Entropía y espontaneidad. Recuperado de: geocities.ws
- Quora. Whats is the practical use of third law of thermodynamics?. Recobrado de: quora.com
- Química general. Tercer principio de la termodinámica. Recuperado de: corinto.pucp.edu.pe
- Third law of thermodynamics. Recuperado de: youtube.com
- Wikipedia. Residual entropy. Recuperado de: en.wikipedia.com
- Wikipedia. Third law of thermodynamics. Recuperado de: en.wikipedia.com
