Energía electromagnética: fórmula, ecuaciones, usos, ejemplos
La energía electromagnética es aquella que se propaga a través de las ondas electromagnéticas (EM). Ejemplo de ello son la luz solar que irradia calor, la corriente que se extrae de la toma eléctrica y la que poseen los rayos X para producir radiografías.
Al igual que las ondas de sonido cuando hacen vibrar el tímpano, las ondas electromagnéticas son capaces de transferir energía que se puede convertir más tarde en calor, corrientes eléctricas o señales diversas.

La energía electromagnética se propaga tanto en un medio material como en el vacío, siempre en forma de onda transversal y hacer uso de ella no es algo nuevo. La luz solar es la fuente primordial de energía electromagnética y la más antigua que se conoce, pero usar electricidad es algo más reciente.
Fue apenas en 1891 cuando Edison Company puso en funcionamiento la primera instalación eléctrica en la Casa Blanca en Washington DC. Y eso como un complemento de las luces a base de gas que se utilizaban en la época, porque al principio hubo bastante escepticismo en cuanto a su uso.
Lo cierto es que aún, en los lugares más recónditos y carentes tendidos eléctricos, la energía electromagnética que llega sin cesar del espacio continuamente sigue manteniendo la dinámica del que llamamos nuestro hogar en el universo.
Índice del artículo
Las ondas electromagnéticas son ondas transversales, en las cuales el campo eléctrico E y el campo magnético B son perpendiculares entre sí, siendo además la dirección de propagación de la onda perpendicular a los campos.
Todas las ondas se caracterizan por su frecuencia. Es el amplio rango de frecuencias de las ondas EM, lo que les confiere versatilidad a la hora de transformar su energía, que es proporcional a la frecuencia.
La figura 2 muestra una onda electromagnética, en ella el campo eléctrico E en azul, oscila en el plano zy, el campo magnético B en rojo lo hace en el plano xy, mientras que la velocidad de la onda se dirige a lo largo del eje +y, de acuerdo al sistema de coordenadas mostrado.
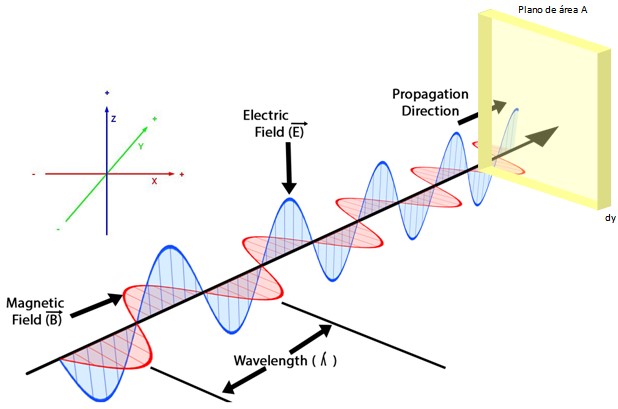
Si en el camino de ambas ondas se interpone una superficie, digamos un plano de área A y espesor dy, tal que sea perpendicular a la velocidad de la onda, el flujo de energía electromagnética por unidad de área, denotado S, se describe a través del vector de Poynting:
S = (1 /μo) E × B
μo es la permeabilidad del vacío (μo = 4π .10-7 Tesla. metro/ampere), una constante relacionada con la facilidad que el medio le brinda a la onda electromagnética para desplazarse.
El vector de Poynting fue introducido por el astrofísico inglés John Henry Poynting en 1884, pionero en el estudio de la energía de los campos eléctricos y magnéticos.
Ahora bien, hay que tomar en cuenta que la energía es un escalar, mientras que S es un vector.
Recordando que la potencia es la energía entregada por unidad de tiempo, entonces el módulo de S indica la potencia instantánea por unidad de área en la dirección de la propagación de la onda electromagnética (tasa de transferencia de energía).
Puesto que E y B son perpendiculares entre sí, el módulo de Ex B es simplemente EB y la potencia instantánea (un escalar) queda como:
S = (1 /μo)EB
Es fácil comprobar que las unidades de S son Watt/m2 en el Sistema Internacional.
Aún hay más. Las magnitudes de los campos E y B están relacionadas entre sí mediante la velocidad de la luz c. De hecho las ondas electromagnéticas en el vacío se propagan así de rápido. Dicha relación es:
E = cB
Sustituyendo esta relación en S se obtiene:
S = (1 /μo.c)E2
El vector de Poynting varía con el tiempo de forma sinusoidal, así que la expresión anterior es su valor máximo, porque la energía entregada por la onda electromagnética también oscila, al igual que lo hacen los campos. Claro que la frecuencia de la oscilación es muy grande, por eso no es posible detectarla en la luz visible, por ejemplo.
De entre los múltiples usos que ya hemos dicho tiene la energía electromagnética, aquí se mencionan dos que se utilizan continuamente en numerosas aplicaciones:
Las antenas están por todas partes llenando el espacio con ondas electromagnéticas. Las hay transmisoras, que transforman señales eléctricas en ondas de radio o de microondas, por ejemplo. Y las hay receptoras, que hacen el trabajo inverso: recogen las ondas y las convierten en señales eléctricas.
Veamos cómo crear una señal electromagnética que se propague en el espacio, a partir de un dipolo eléctrico. El dipolo consiste en dos cargas eléctricas de igual magnitud y signos contrarios, separadas por una pequeña distancia.
En la siguiente figura está el campo eléctrico E cuando la carga + está arriba (figura izquierda). E apunta hacia abajo en el punto mostrado.

En la figura 3 derecha, el dipolo cambió de posición y ahora E apunta hacia arriba. Repitamos este cambio muchas veces y muy rápido, digamos con una frecuencia f. Se crea así un campo E variable en el tiempo da lugar a un campo magnético B, también variable y cuya forma es senoidal (ver figura 4 y más abajo el ejemplo 1).
Y como la ley de Faraday asegura que un campo magnético B variable en el tiempo da lugar a un campo eléctrico, pues resulta que haciendo oscilar el dipolo ya se tiene un campo electromagnético capaz de propagarse en el medio.

Note que B apunta hacia dentro o hacia fuera de la pantalla alternadamente (siempre es perpendicular a E).
Los condensadores tienen la virtud de almacenar carga eléctrica y por consiguiente energía eléctrica. Forman parte de numerosos dispositivos: motores, circuitos de radio y televisión, sistema de luces de los automóviles y mucho más.
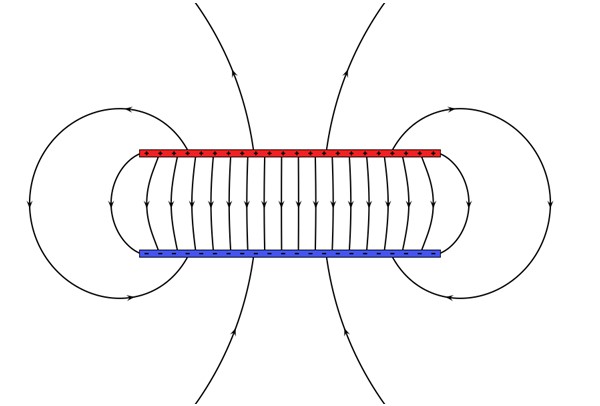
Los condensadores constan de dos conductores separados una pequeña distancia. A cada uno se le confiere una carga de igual magnitud y signo contrario, creándose entonces un campo eléctrico en el espacio entre ambos conductores. La geometría puede variar, siendo una muy conocida la del condensador de placas plano-paralelas.
La energía almacenada en un condensador proviene del trabajo que se hizo para cargarlo, el cual sirvió para crear el campo eléctrico en su interior. Introduciendo un material dieléctrico entre las placas, la capacidad del condensador aumenta y por lo tanto la energía que este puede almacenar.
Un condensador de capacidad C y descargado inicialmente, que se cargue mediante una batería que suministra un voltaje V, hasta alcanzar una carga Q, almacena una energía U dada por:
U = ½ (Q2/C) = ½ QV = ½ CV2
Con anterioridad se dijo que la magnitud del vector de Poynting equivale a la potencia que la onda entrega por cada metro cuadrado de superficie, y que además, al ser el vector dependiente del tiempo, su valor oscilaba hasta un máximo de S = S = (1 /μo.c)E2.
El valor promedio de S en un ciclo de la onda es fácil de medir e indicativo de la energía de la onda. A este valor se lo conoce como intensidad de la onda y se calcula de esta forma:
I = Smedia =S = (1 /μo.c)E2medio
Una onda electromagnética se representa mediante una función senoidal:
E = Eo sen (kx – ωt)
Donde Eo es la amplitud de la onda, k el número de onda y ω la frecuencia angular. Entonces:

Se tiene una estación de radio que transmite una señal de 10 kW de potencia y frecuencia de 100 MHz, la cual se propaga en forma esférica, como en la figura de arriba.
Encontrar: a) la amplitud de los campos eléctricos y magnéticos en un punto ubicado a 1 km de la antena y b) la energía electromagnética total que incide sobre una lámina cuadrada de lado 10 cm en un lapso de 5 minutos.
Los datos son:
Velocidad de la luz en el vacío: c= 300.000 km/s
Permeabilidad del vacío: μo = 4π .10-7 T.m/A (Tesla. metro/ampere)
Solución a
Se utiliza la ecuación dada en el ejemplo 1 para encontrar la intensidad de la onda electromagnética, pero antes hay que expresar los valores en el Sistema Internacional:
10 kW = 10000 W
100 MHz = 100 x 106 Hz
Enseguida se sustituyen estos valores en la ecuación para la intensidad, puesto que se trata de una fuente que emite por igual a todos lados (fuente isotrópica):
Anteriormente se dijo que las magnitudes de E y B estaban relacionadas por la velocidad de la luz:
E = cB
B= (0.775 /300.000.000) T = 2.58 x 10-9 T
Solución b
Smedio es potencia por unidad de área y a su vez la potencia es energía por unidad de tiempo. Multiplicando Smedio por el área de la placa y por el tiempo de exposición, se obtiene el resultado pedido:
5 minutos = 300 segundos
Área = (10/100)2 m2 = 0.01 m2.
U = 0.775 x 300 x 0.01 Joules = 2.325 Joules.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 6. Electromagnetismo. Editado por Douglas Figueroa (USB). 307-314.
- ICES (International Committee on Electromagnetic Safety). Electromagnetic Energy Facts, and a Qualitative View. Recobrado de: ices-emfsafety.org.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson. 893 – 896.
- Portland State University. EM waves transport energy. Recobrado de: pdx.edu
- What is Electromagnetic Energy and Why is it Important?. Recobrado de: sciencestruck.com.
