Energía gravitacional: fórmulas, características, aplicaciones, ejercicios
La energía gravitacional es la que tiene un objeto masivo cuando está inmerso en el campo gravitacional producido por otro. Algunos ejemplos de objetos con energía gravitacional son: la manzana en el árbol, la manzana cayendo, la Luna orbitando la Tierra y la Tierra orbitando el Sol.
Isaac Newton (1642-1727) fue el primero en darse cuenta que la gravedad es un fenómeno universal y que todo objeto con masa produce en su entorno un campo capaz de producir una fuerza sobre otro.

Índice del artículo
- 1 Fórmulas y ecuaciones
- 2 Características de la energía gravitatoria
- 3 Aplicaciones
- 4 Ejercicios
- 5 Referencias
La fuerza a la que se refería Newton se conoce como fuerza gravitacional y le proporciona energía al objeto sobre el que actúa. Newton formuló la ley de gravitación universal de la siguiente manera:
“Sean dos objetos puntuales de masas m1 y m2 respectivamente, cada uno ejerce sobre el otro una fuerza de atracción que es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa”.
La energía gravitacional U asociada a la fuerza gravitacional F es:
Un objeto que está inmerso en un campo gravitacional tiene energía potencial gravitacional U y energía cinética K. Si no hay otras interacciones, o son de intensidad despreciable, la energía total E de dicho objeto es la suma de su energía gravitacional más su energía cinética:
E = K + U
Si un objeto está en un campo gravitatorio y no están presentes otras fuerzas de tipo disipativo, como la fricción o la resistencia al aire, entonces la energía total E es una cantidad que se mantiene constante durante el movimiento.
– Un objeto tiene energía potencial gravitatoria si solo está en la presencia del campo gravitacional producido por otro.
– La energía gravitatoria entre dos objetos crece en la medida que la distancia de separación entre los mismos es mayor.
– El trabajo realizado por la fuerza gravitatoria es igual y contrario a la variación de la energía gravitacional de la posición final respecto a la de su posición inicial.
– Si un cuerpo está sometido únicamente a la acción de la gravedad, entonces la variación de su energía gravitatoria es igual y contraria a la variación de su energía cinética.
– La energía potencial de un objeto de masa m que se encuentra a una altura h respecto a la superficie terrestre es mgh veces mayor que la energía potencial en la superficie, siendo g la aceleración de gravedad, para alturas h mucho menores que el radio terrestre.
El campo gravitatorio g se define como la fuerza gravitacional F por unidad de masa. Se determina colocando una partícula de prueba m en cada punto del espacio y calculando el cociente entre la fuerza que actúa sobre la partícula de prueba dividida entre el valor de su masa:
g = F / m
Se define el potencial gravitatorio V de un objeto de masa m como la energía potencial gravitacional de ese objeto dividida entre su propia masa.
La ventaja de esta definición es que el potencial gravitatorio sólo depende del campo gravitatorio, de modo que una vez conocido el potencial V, la energía gravitacional U de un objeto de masa m es:
U = m.V
La energía potencial gravitatoria es la que almacenan los cuerpos cuando están en un campo gravitacional.
Por ejemplo, el agua contenida en un tanque tiene más energía en la medida que el tanque está a mayor altura.
A mayor altura del tanque, mayor será la velocidad de salida del agua por el grifo. Esto es debido a que la energía potencial del agua a la altura del tanque se transforma en energía cinética del agua en la salida del grifo.
Cuando el agua se represa en lo alto de una montaña, esa energía potencial puede ser aprovechada para hacer girar las turbinas de generación eléctrica.
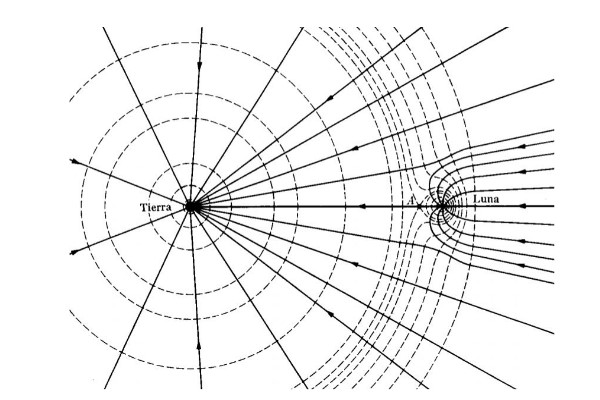
La energía gravitacional también explica las mareas. Como la energía y la fuerza gravitacional dependen de la distancia, el tirón gravitacional de la Luna es mayor en la cara de la Tierra más cercana a la Luna que la cara más lejana y opuesta.
Esto produce una diferencia de fuerzas que deforma la superficie del mar. El efecto es mayor en luna nueva, cuando el Sol y la Luna están alineados.
La posibilidad de construir estaciones espaciales y satélites que se mantengan relativamente cercanos a nuestro planeta, es debida a energía gravitacional que produce la Tierra. De no ser así las estaciones espaciales y los satélites artificiales quedarían vagando por el espacio.
Suponga que la Tierra tiene masa M y un objeto que está por encima de la superficie terrestre a la distancia r respecto al centro de la misma tiene masa m.
En este caso el potencial gravitacional se determina a partir de la energía gravitatoria simplemente dividiendo entre la masa del objeto resultando:
Supongamos que la Tierra tiene radio RT y masa M.
Aun cuando la Tierra no es un objeto puntual el campo sobre su superficie es equivalente al que se obtendría si toda su masa M estuviese concentrada en el centro, de modo que la energía gravitatoria de un objeto a altura h sobre la superficie terrestre es
U(RT + h) = -G.M m (RT + h)^-1
Pero debido a que h es mucho menor que RT, la expresión anterior puede aproximarse por
U = Uo + mgh
Donde g es la aceleración de gravedad, cuyo valor promedio para la Tierra es 9.81 m/s^2.
Entonces la energía potencial Ep de un objeto de masa m a la altura h sobre la superficie terrestre es:
Ep(h) = U +Uo = mgh
Sobre la superficie terrestre h=0, por lo que un objeto sobre la superficie tiene Ep = 0. Los cálculos detallados pueden verse en la figura 3.

Suponga que nuestro planeta sufre un colapso gravitacional por pérdida de energía térmica en su interior y su radio decae hasta la mitad del valor actual pero se mantiene constante la masa del planeta.
Determine cuál sería la aceleración de gravedad cerca de la superficie de la Nueva Tierra y cuánto pesaría un superviviente que pesaba 50 kg-f antes del colapso. Aumenta o disminuye la energía gravitacional de la persona y en qué factor.
Solución
La aceleración de gravedad en la superficie de un planeta depende de su masa y de su radio. La constante de gravitación es universal y sirve por igual para planetas y exoplanetas.
En el caso que se nos plantea, si se reduce el radio de la Tierra a la mitad entonces la aceleración de gravedad de la Nueva Tierra sería 4 veces mayor. Los detalles pueden verse en la pizarra siguiente.
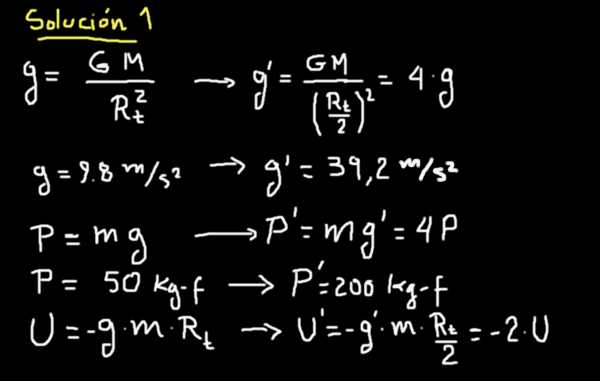
Esto significa que un superhombre y superviviente que en el viejo planeta pesaba 50 kg-f pesará 200 kg-f en el nuevo planeta.
Por otra parte, la energía gravitacional se habrá reducido a la mitad en la superficie del nuevo planeta.
En referencia a la situación planteada en el ejercicio 1, ¿qué pasaría con la velocidad de escape: aumenta, disminuye, en qué factor?
Solución 2
La velocidad de escape es la velocidad mínima necesaria para escapar de la atracción gravitacional de un planeta.
Para calcularla se supone que un proyectil que se dispara con esta velocidad llega al infinito con velocidad cero. Además, en el infinito la energía gravitacional es nula. Por lo tanto un proyectil que se dispare con la velocidad de escape tendrá energía total cero.
Es decir que en la superficie del planeta al momento del disparo la suma de la energía cinética del proyectil + la energía gravitacional debe ser nula:
½ m Ve^2 – (G M.m)/RT = 0
Note que la velocidad de escape no depende de la masa del proyectil y su valor al cuadrado es
Ve^2 = (2G M) / RT
Si el planeta colapsa hasta un radio mitad del original el cuadrado de la nueva velocidad de escape pasa a ser el doble.
Por lo tanto la nueva velocidad de escape crece y pasa a ser 1.41 veces la vieja velocidad de escape:
Ve’ = 1.41 Ve
Un chico en el balcón de un edificio a 30 metros de suelo suelta una manzana de 250 g, que al cabo de algunos segundos llega al suelo.

a) ¿Cuál es la diferencia de energía gravitacional de la manzana en lo alto respecto a la manzana a nivel del suelo?
b) ¿Qué rapidez tenía la manzana justo antes desparramarse en el suelo?
c) ¿Qué pasa con la energía una vez que la manzana se aplastó contra el suelo?
Solución
a) La diferencia de energía gravitacional es
m.g.h = 0.250 kg * 9.81 m/s^2 * 30 m = 73.6 J
b) La energía potencial que tenía la manzana cuando estaba a 30 m de altura se transforma en energía cinética para cuando la manzana llegue al suelo.
½ m v^2 = m.g.h
v^2 = 2.g.h
Al sustituir valores y despejar, se deduce que la manzana llega al suelo con una rapidez de 24.3 m/s = 87.3 km/h.
c) Obviamente la manzana se desperdiga y toda la energía gravitatoria acumulada al comienzo se pierde en forma de calor, ya que los trozos de manzana y la zona de impacto se calientan, además parte de la energía se disipa también en forma de ondas sonoras “splash”.
- Alonso, M. (1970). Física Vol. 1, Fondo Educativo Interamericano.
- Hewitt, Paul. 2012. Conceptual Physical Science. 5th. Ed. Pearson.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Sears, F. (2009).Física Universitaria Vol. 1
- Wikipedia. Energía gravitatoria. Recuperado de: es.wikipedia.com
- Wikipedia. Gravitational energy. Recuperado de: en.wikipedia.com
