Diferencia de cubos: fórmulas, ecuaciones, ejemplos, ejercicios
La diferencia de cubos es una expresión algebraica binomial de la forma a3 – b3, donde los términos a y b pueden ser números reales o también expresiones algebraicas de diversos tipos. Un ejemplo de diferencia de cubos es: 8 – x3, ya que 8 se puede escribir como 23.
Geométricamente podemos pensar en un cubo grande, de lado a, al cual se le resta el cubo pequeño de lado b, como se ilustra en la figura 1:
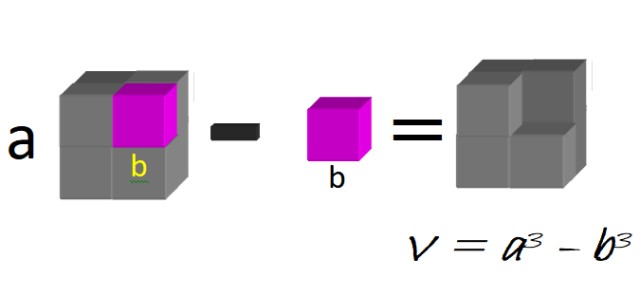
El volumen de la figura resultante es precisamente una diferencia de cubos:
V = a3 – b3
Para encontrar una expresión alternativa se observa que esta figura se puede descomponer en tres prismas, como se muestra a continuación:

Un prisma tiene un volumen dado por el producto de sus tres dimensiones: ancho x alto x profundidad. De esta manera, el volumen resultante es:
V = a3 – b3 = a2.b + b3 + a.b2
El factor b es común a la derecha. Además, en la figura mostrada arriba se cumple en particular que:
b = (a/2) ⇒ a = b + b
Por lo tanto puede decirse que: b = a – b. De esta forma:
a3 – b3 = b (a2 + b2 +a.b) = (a-b) (a2 + a.b + b2)
Esta manera de expresar la diferencia de cubos demostrará ser muy útil en multitud de aplicaciones y se habría obtenido de igual forma, aunque el lado del cubo faltante en la esquina fuera diferente a b = a/2.
Nótese que el segundo paréntesis se parece mucho al producto notable del cuadrado de la suma, pero el término cruzado no está multiplicado por 2. El lector puede desarrollar el lado derecho para verificar que efectivamente se obtiene a3 – b3.
Índice del artículo
Hay varias diferencias de cubos:
1 – m6
a6b3 – 8z12y6
(1/125).x6 – 27.y9
Analicemos cada una de ellas. En el primer ejemplo, el 1 se puede escribir como 1 = 13 y el término m6 queda: (m2)3. Ambos términos son cubos perfectos, por lo tanto su diferencia es:
1 – m6 = 13 – (m2)3
En el segundo ejemplo se reescriben los términos:
a6b3 = (a2b)3
8z12y6 = 23 (z4)3 (y2)3 = (2z4y2)3
La diferencia de estos cubos queda: (a2b)3 – (2z4y2)3.
Por último, la fracción (1/125) es (1/53), x6 = (x2)3, 27 = 33 y y9 = (y3)3. Sustituyendo todo esto en la expresión original, se obtiene:
(1/125).x6 – 27y9 = [(1/5) (x2)]3 – (3y3)3
Factorizar la diferencia de cubos simplifica muchas operaciones algebraicas. Para ello basta con usar la fórmula deducida anteriormente:

Ahora bien, el procedimiento para aplicar esta fórmula consta de tres pasos:
– En primer lugar se obtiene la raíz cúbica de cada uno de los términos de la diferencia.
– Después se construyen el binomio y el trinomio que aparecen en el lado derecho de la fórmula.
– Finalmente se sustituyen el binomio y el trinomio para obtener la factorización definitiva.
Ilustremos el uso de estos pasos con cada uno de los ejemplos de diferencia de cubos propuestos arriba y obtengamos así su equivalente factorizado.
Ejemplo 1
Factorizar la expresión 1 – m6 siguiendo los pasos descritos. Comenzamos reescribiendo la expresión como 1 – m6 = 13 – (m2)3 para extraer las respectivas raíces cúbicas de cada término:
Seguidamente se construyen el binomio y el trinomio:
a = 1
b = m2
Entonces:
a – b = 1 – m2
(a2 +a.b + b2) = 12 + 1.m2 + (m2)2 = 1 + m2 + m4
Por último se sustituye en la fórmula a3 – b3 = (a-b) (a2 +a.b + b2):
1 – m6 = (1 – m2) (1 + m2 + m4)
Ejemplo 2
Factorizar:
a6b3 -8z12y6 = (a2b)3 – (2z4y2)3
Puesto que se trata de cubos perfectos, las raíces cúbicas son inmediatas: a2b y 2z4y2, de allí se sigue que:
– Binomio: a2b – 2z4y2
– Trinomio: (a2b)2 + a2b. 2z4y2 + (a2b +2z4y2)2
Y ahora se construye la factorización deseada:
a6b3 -8z12y6 = (a2b – 2z4y2). [(a2b)2 + a2b. 2z4y2 + (a2b + 2z4y2)2] =
= (a2b – 2z4y2). [a4b2 + 2a2b.z4y2 + (a2b + 2z4y2)2]
En principio está lista la factorización, pero con frecuencia es necesario simplificar cada término. Entonces se desarrolla el producto notable –cuadrado de una suma- que aparece al final y después sumar términos semejantes. Recordando que el cuadrado de una suma es:
(x + y)2 = x2 + 2xy + y2
El producto notable a la derecha se desarrolla de esta forma:
(a2b + 2z4y2)2 = a4b2 + 4a2b.z4y2 + 4z8y4
Sustituyendo el desarrollo obtenido en la factorización de la diferencia de cubos:
a6b3 -8z12y6 = (a2b – 2z4y2). [a4b2 + 2a2b.z4y2 + a4b2 + 4a2b.z4y2 + 4z8y4] =
Finalmente, agrupando términos semejantes y factorizando los coeficientes numéricos, que son todos pares, se obtiene:
(a2b – 2z4y2). [2a4b2 + 6a2b.z4y2 + 4z8y4] = 2(a2b – 2z4y2). [a4b2 + 3a2b.z4y2 + 2z8y4]
Ejemplo 3
Factorizar (1/125).x6 – 27y9 es bastante más sencillo que el caso anterior. Primero se identifican los equivalentes de a y de b:
a = (1/5)x2
b = 3y3
Después se sustituyen directamente en la fórmula:
(1/125).x6 – 27y9 = [(1/5)x2 – 3y3]. [(1/25)x4 + (3/5)x2y3 + 9y6]
La diferencia de cubos tiene, como hemos dicho, variedad de aplicaciones en el Álgebra. Veamos algunas:
Resolver las siguientes ecuaciones:
a) x5 – 125 x2 = 0
b) 64 – 729 x3 = 0
Solución a
Primero se factoriza la ecuación de esta forma:
x2 (x3 – 125) = 0
Como 125 es un cubo perfecto, el paréntesis se escribe como una diferencia de cubos:
x2 . (x3 – 53) = 0
La primera solución es x = 0, pero encontramos más si hacemos x3 – 53 = 0, entonces:
x3 = 53 → x = 5
Solución b
Se reescribe el lado izquierdo de la ecuación como 64 – 729 x3 = 43 – (9x)3. Por lo tanto:
43 – (9x)3 = 0
Ya que el exponente es el mismo:
9x = 4 → x = 9/4
Factorizar la expresión:
(x + y)3 – (x – y)3
Solución
Esta expresión es una diferencia de cubos, si en la fórmula de la factorización notamos que:
a = x+ y
b = x- y
Entonces se construye primero el binomio:
a – b = x+ y – (x- y) = 2y
Y ahora el trinomio:
a2 + a.b + b2 = (x+ y)2 + (x+y)(x-y) + (x-y)2
Se desarrollan los productos notables:
(x+ y)2 = x2 + 2xy +y2
(x+y)(x-y) = x2– y2
(x- y)2 = x2 – 2xy +y2
Enseguida hay que sustituir y reducir los términos semejantes:
a2 + a.b + b2 = x2 + 2xy +y2+ x2– y2+ x2 – 2xy +y2 = 3x2 + y2
La factorización resulta en:
(x + y)3 – (x – y)3 = 2y. (3x2 + y2)
- Baldor, A. 1974. Álgebra. Editorial Cultural Venezolana S.A.
- CK-12 Foundation. Suma y diferencia de cubos. Recuperado de: ck12.org.
- Khan Academy. Factorización de diferencias de cubos. Recuperado de: es.khanacademy.org.
- Math is Fun Advanced. Difference of two cubes. Recuperado de: mathsisfun.com
- UNAM. Factorización de una diferencia de cubos. Recuperado de: dcb.fi-c.unam.mx.
