¿Qué es el equilibrio dinámico? (Con ejemplo)
El equilibrio dinámico es el estado en que se encuentra un objeto móvil representado idealmente como una partícula cuando su movimiento es rectilíneo uniforme. Este fenómeno se produce cuando la sumatoria de fuerzas externas que actúan sobre él se anula.
Suele creerse que si no existe una fuerza neta o resultante sobre un objeto, el reposo es la única consecuencia posible. O también que para que un cuerpo esté en equilibrio no debe haber fuerza alguna actuando.
En realidad el equilibrio es ausencia de aceleración, y por lo tanto la velocidad constante es perfectamente posible. El gato de la figura puede estar moviéndose sin aceleración.
Un objeto que posea movimiento circular uniforme no se encuentra en equilibrio dinámico. Pese a que su rapidez es constante, existe una aceleración dirigida hacia el centro de la circunferencia que lo mantiene en la trayectoria. Esta aceleración se encarga de ir cambiando adecuadamente al vector velocidad.
La velocidad nula es una situación particular del equilibrio de una partícula, equivalente a afirmar que el objeto está en reposo.
En cuanto a considerar a los objetos como partícula, se trata de una idealización muy útil a la hora de describir su movimiento global. En realidad los objetos móviles que nos rodean están compuestos por una gran cantidad de partículas cuyo estudio individual resultaría engorroso.
Índice del artículo
Este principio permite sustituir la acción de múltiples fuerzas sobre un objeto por una equivalente llamada fuerza resultante FR o fuerza neta FN y que en este caso es nula:
F1+ F2 + F3 +…. = FR = 0
Donde las fuerzas F1, F2, F3…., Fi son las diferentes fuerzas que actúan sobre el cuerpo. La notación de sumatoria es una manera compacta de expresarlo:
Siempre y cuando no intervenga una fuerza no equilibrada, el objeto puede mantenerse indefinidamente moviéndose con velocidad constante, dado que solo una fuerza puede alterar este panorama.
En términos de las componentes de la fuerza resultante, la condición de equilibrio dinámico de una partícula queda expresada así: Fx = 0; Fy = 0; Fz = 0.
Para el modelo de partícula, la condición FR = 0 es suficiente garantía de equilibrio. Sin embargo, al tomar en cuenta las dimensiones del móvil en estudio, está la posibilidad de que el objeto pueda rotar.
El movimiento de rotación implica la existencia de una aceleración, por lo tanto los cuerpos que rotan no se encuentran en equilibrio dinámico. El giro de un cuerpo necesita no solo de la participación de una fuerza, sino que es necesario aplicarla el sitio conveniente.
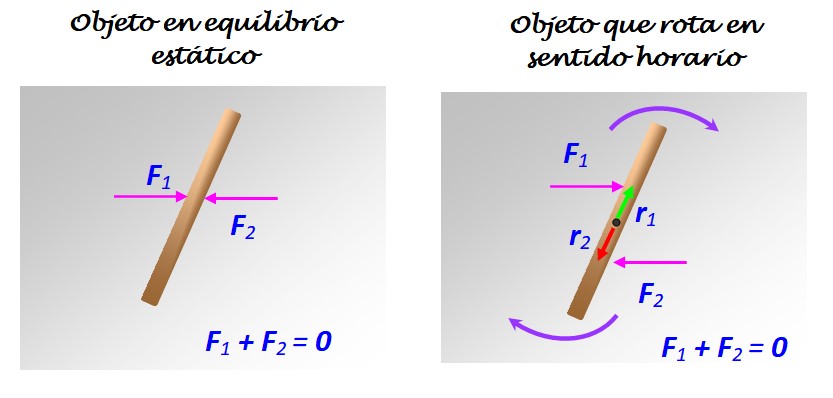
Para comprobarlo, se puede colocar una varilla delgada de longitud sobre una superficie libre de rozamientos, como por ejemplo una superficie helada o un espejo o vidrio muy pulido. La normal equilibra al peso en sentido vertical, y al aplicar en horizontal dos fuerzas F1 y F2 de la misma magnitud, según el diagrama de la siguiente figura, se comprueba lo que ocurre:
Si F1 y F2 se aplican como se muestra a la izquierda, con una línea de acción común, la varilla permanecerá en reposo. Pero si F1 y F2 se aplican según se muestra a la derecha, con distintas líneas de acción, aunque paralelas, ocurre una rotación en sentido horario, alrededor del eje que pasa por el centro.
En tal caso, F1 y F2 constituyen un par de fuerzas o simplemente un par.
El efecto del par consiste en producir una rotación sobre un objeto extendido como la varilla del ejemplo. La magnitud vectorial encargada se denomina torque o también momento de una fuerza. Se denota como τ y se calcula mediante:
τ = r x F
En esta expresión F es la fuerza aplicada y r es el vector que va desde el eje de giro hasta el punto de aplicación de la fuerza (ver la figura 2). La dirección de τ siempre es perpendicular al plano donde yacen F y r y sus unidades en sistema internacional son N.m.
Para el ejemplo, la dirección de los momentos producidos por F1 y F2 es hacia el papel, de acuerdo a las reglas del producto vectorial.
Aunque las fuerzas se anulan entre sí, sus torques no. Y el resultado es la rotación mostrada.
Son dos condiciones que deben cumplirse para garantizar el equilibrio de un objeto extendido:
Se tiene un cajón o baúl que pesa 16 kg-f, el cual desliza por un plano inclinado con velocidad constante. El ángulo de inclinación de la cuña es θ = 36º. Responder:
a) ¿Cuál es la magnitud de la fuerza de roce dinámico necesaria para que el baúl deslice con velocidad constante?
b) ¿Cuánto vale el coeficiente de rozamiento cinético?
c) Si la altura h del plano inclinado es de 3 metros, encontrar la velocidad de descenso del baúl sabiendo que tarda 4 segundos en llegar al suelo.
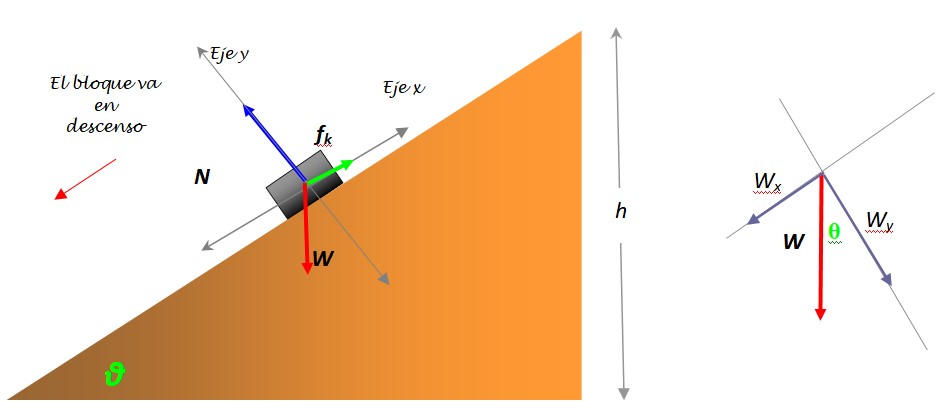
El baúl puede tratarse como si fuera una partícula. Por ello se aplicarán las fuerzas en un punto ubicado aproximadamente en su centro, sobre el cual se puede suponer concentrada toda su masa. Es a este punto al que se le seguirá la pista.
El peso W es la única fuerza que no cae sobre uno de los ejes coordenados y debe ser descompuesta en dos componentes: Wx y Wy. Esta descomposición se muestra en el esquema (figura 3).
También conviene pasar el peso a unidades del sistema internacional, para lo cual basta con multiplicar por 9.8:
Wy = W.cosθ = 16 x 9.8 x cos 36º N = 126.9 N
Wx = W.senθ = 16 x 9.8 x sen 36º = 92.2 N
Apartado a
A lo largo del eje horizontal están la componente horizontal del peso Wx y la fuerza de roce dinámico o cinético fk, que se opone al movimiento.
Eligiendo el sentido positivo en la dirección del movimiento, es sencillo advertir que es Wx la responsable de que el bloque vaya cuesta abajo. Y como el rozamiento se opone, en vez de resbalar aceleradamente, el bloque tiene la posibilidad de ir deslizando con rapidez constante cuesta abajo.
La primera condición de equilibrio es suficiente, puesto que estamos tratando al baúl como a una partícula, que se nos asegura en el enunciado que está en equilibrio dinámico:
Wx – fk = 0 (no hay aceleración en la dirección horizontal)
fk = 92.2 N
Apartado b
La magnitud del roce dinámico es constante y está dada por fk = μk N. Esto significa que la fuerza de rozamiento dinámico es proporcional a la normal y se requiere la magnitud de esta para conocer el coeficiente de rozamiento.
Observando el diagrama de cuerpo libre se aprecia que sobre el eje vertical tenemos la fuerza normal N, que la cuña ejerce sobre el baúl y está dirigida hacia arriba. Ella está equilibrada con la componente vertical del peso Wy. Seleccionando hacia arriba como sentido positivo y haciendo uso de la segunda ley de Newton y la condición de equilibrio resulta:
N – Wy = 0 (no hay movimiento a lo largo del eje vertical)
Por lo tanto:
N = Wy = 126.9 N
fk = μk N
μk = fk / N=92.2 /126.9= 0.73
Apartado c
La distancia total recorrida por el baúl desde el tope de la cuña hasta el suelo se encuentra mediante trigonometría:
d= h/sen 36º = 3/sen 36º m = 5.1 m.
Para calcular la velocidad se emplea la definición para movimiento rectilíneo uniforme:
v = d/t = 5.1 m/4 s = 1.3 m/s
- Rex, A. 2011. Fundamentos de Física. Pearson. 76 – 90.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning. 120 – 124.
- Serway, R., Vulle, C. 2011. Fundamentos de Física. 9na Ed. Cengage Learning. 99-112.
- Tippens, P. 2011. Física: Conceptos y Aplicaciones. 7ma Edición. MacGraw Hill. 71 – 87.
- Walker, J. 2010. Physics. Addison Wesley. 148-164.