Tipos de integrales
Los tipos de integrales que nos encontramos en el cálculo son las integrales indefinidas y las integrales definidas. Aunque las integrales definidas tienen muchas más aplicaciones que las integrales indefinidas, es necesario primero aprender a resolver integrales indefinidas.
Una de las aplicaciones más atractivas de las integrales definidas es el cálculo del volumen de un sólido de revolución. Ambos tipos de integrales poseen las mismas propiedades de linealidad y además las técnicas de integración no dependen del tipo de integral.
Pero a pesar de ser muy parecidos, existe una diferencia principal; en el primer tipo de integral el resultado es una función (la cual no es específica) mientras que en el segundo tipo el resultado es un número.
Tipos básicos de integrales
El mundo de las integrales es muy amplio, pero dentro de éste podemos distinguir dos tipos básicos de integrales, las cuales tienen una gran aplicabilidad en la vida cotidiana.
1- Integrales indefinidas
Si F''(x)=f(x) para todo x en el dominio de f, decimos que F(x) es una antiderivada, una primitiva o una integral de f(x).
Por otro lado, observemos que (F(x)+C)’=F''(x)=f(x), lo cual implica que la integral de una función no es única, pues dando diferentes valores a la constante C obtendremos diferentes antiderivadas.
Por esta razón F(x)+C es llamada la Integral Indefinida de f(x) y C es llamada constante de integración y lo escribimos de la siguiente manera:

Como podemos ver, la integral indefinida de la función f(x) es una familia de funciones.
Por ejemplo, si se quiere calcular la integral indefinida de la función f(x)=3x², primero se debe hallar una antiderivada de f(x).
Es fácil notar que F(x)=x³ es una antiderivada, ya que F''(x)=3x². Por lo tanto, se puede concluir que
∫f(x)dx=∫3x²dx=x³+C.
2- Integrales definidas
Sea y=f(x) una función real, continua en un intervalo cerrado [a,b] y sea F(x) una antiderivada de f(x). Se llama integral definida de f(x) entre los límites a y b al número F(b)-F(a), y se denota como sigue:
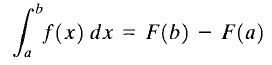
La fórmula mostrada arriba es mejor conocida como “El Teorema Fundamental del Cálculo”. Aquí “a” es llamado límite inferior y “b” es llamado límite superior. Como se puede ver, la integral definida de una función es un número.
En este caso, si se calcula la integral definida de f(x)=3x² en el intervalo [0,3], se obtendrá un número.
Para determinar dicho número escogemos F(x)=x³ como antiderivada de f(x)=3x². Luego, calculamos F(3)-F(0) lo cual nos arroja como resultado 27-0=27. En conclusión, la integral definida de f(x) en el intervalo [0,3] es 27.
Se puede destacar que si se escoge G(x)=x³+3, entonces G(x) es una antiderivada de f(x) distinta a F(x), pero esto no afecta el resultado pues G(3)-G(0)=(27+3)-(3)=27. Por esta razón, en las integrales definidas no aparece la constante de integración.
Una de las aplicaciones más útiles que posee este tipo de integral es que permite calcular el área (volumen) de una figura plana (de un sólido de revolución), estableciendo funciones y límites de integración adecuados (y un eje de giro).
Dentro de las integrales definidas podemos encontrar diversas extensiones de ésta como por ejemplo integrales de línea, integrales de superficie, integrales impropias, integrales múltiples, entre otras, todas con aplicaciones muy útiles en las ciencias e ingeniería.
Referencias
- Kishan, H. (2005). Integral Calculus. Atlantic Publishers & Distributors.
- Purcell, E. J., Varberg, D., & Rigdon, S. E. (2007). Cálculo (Novena ed.). Prentice Hall.
