Lente divergente: características, elementos, tipos, aplicaciones
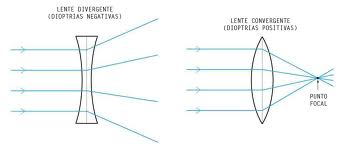
Las lentes divergentes son aquellas que son más delgadas en su parte central y más gruesas en los bordes. Como consecuencia de ello, separan (hacen divergir) los rayos de luz que inciden sobre ellas de forma paralela al eje principal. Sus prolongaciones acaban convergiendo en el foco imagen situado a la izquierda de la lente.
Las lentes divergentes, o negativas como también se las conoce, forman lo que se denomina imágenes virtuales de los objetos. Cuentan con diversas aplicaciones. En particular, en oftamología se emplean para corregir la miopía y algunos tipos de astigmatismo.

De modo que, si sufres de miopía y utilizas gafas, tienes a mano un ejemplo perfecto de lente divergente.
Índice del artículo
- 1 Características de las lentes divergentes
- 2 Elementos de las lentes divergentes
- 3 Formación de imágenes
- 4 Aplicaciones
- 5 Tipos
- 6 Diferencias con las lentes convergentes
- 7 Ecuación de Gauss de las lentes y aumento de una lente
- 8 Ejercicio resuelto
- 9 Referencias
Tal y como se ha explicado anteriormente las lentes divergentes son más estrechas en su parte central que en los bordes. Además, en este tipo de lentes una de sus superficies siempre es cóncava. Esto les confiere a este tipo de lentes una serie de características.
Para empezar, la prolongación de los rayos que inciden sobre ellas da como resultado imágenes virtuales que no se pueden recoger en ningún tipo de pantalla. Esto es así, porque los rayos que atraviesan la lente no convergen en ningún punto, ya que divergen en todas las direcciones. Además, según sea la curvatura de la lente los rayos se abrirán en mayor o menor medida.
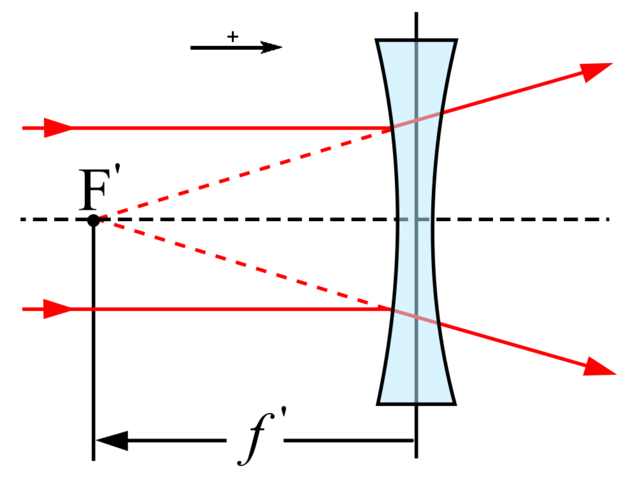
Otra característica importante de este tipo de lentes es que el foco se encuentra a la izquierda de la lente, de modo que está entre esta y el objeto.
Además, en las lentes divergentes las imágenes son más reducidas que el objeto y se encuentran entre este y el foco.
A la hora de estudiarlas, es esencial conocer qué elementos que constituyen las lentes en general y las lentes divergentes en particular.
Se denomina centro óptico de una lente al punto a través del cual los rayos no experimentan ninguna desviación. El eje principal, por su parte, es la recta que une dicho punto y el foco principal, estando representado este último con la letra F.
Recibe el nombre foco principal el punto en el que se encuentran todos los rayos que inciden en la lente de forma paralela al eje principal.
De este modo, se denomina distancia focal la distancia existente entre el centro óptico y el foco.
Los centros de curvatura se definen como los centros de las esferas que crean la lente; siendo, de este modo, los radios de curvatura los radios de las esferas que dan origen a la lente. Y ya, por último, se llama plano óptico al plano central de la lente.
Para determinar gráficamente la formación de una imagen en una lente delgada únicamente es necesario conocer la dirección que seguirán dos de los tres rayos
cuya trayectoria se conoce.
Uno de ellos es el que incide en la lente de forma paralela al eje óptico de la lente. Este, una vez refractado en la lente, pasará por el foco imagen. El segundo de los rayos cuya trayectoria es conocida es el que atraviesa el centro óptico. Este no verá modificada su trayectoria.
El tercero y último es el que pasa por el foco objeto (o bien su prolongación atraviesa el foco objeto) el cual después de refractarse seguirá una dirección paralela a la del eje óptico de la lente.
De esta forma, en general, en las lentes se formará un tipo de imagen u otra dependiendo de la posición del objeto o cuerpo respecto de la lente.
Sin embargo, en el caso particular de las lentes divergentes, sea cual sea la posición del cuerpo frente a la lente, la imagen que se formará tendrá unas características determinadas. Y es que en las lentes divergentes la imagen siempre será virtual, de menor tamaño que el cuerpo y derecha.
El hecho de que puedan separar la luz que las atraviesa otorga a las lentes divergentes unas interesantes cualidades dentro del ámbito de la óptica. De esta forma, pueden corregir la miopía y algunos tipos concretos de astigmatismo.
Las lentes divergentes oftálmicas separan los rayos de luz para que cuando lleguen al ojo humano estén más distanciados. Así, cuando atraviesan la cornea y el cristalino llegan más lejos y pueden alcanzar la retina corriendo los problemas de visión de las personas que sufren miopia.
Como ya hemos comentado, las lentes convergentes tienen al menos una superficie cóncava. Debido a esto, existen tres tipos de lentes divergentes: bicóncavas, planocóncavas y convexo-cóncavas.
Las lentes divergentes bicóncavas están formadas por dos superficies cóncavas, las planocóncavas cuentan con una superficie cóncava y otra plana, mientras que en las convexo-cóncavas o menisco divergentes una superficie es ligeramente convexa y la otra es cóncava.
En las lentes convergentes, al contrario de lo que ocurre en las divergentes, el espesor disminuye desde el centro hacia los bordes. Así, en este tipo de lentes los rayos de luz que inciden de forma paralela al eje principal se concentran o convergen en único punto (en el foco). De esta forma, siempre crean imágenes reales de los objetos.
En óptica, las lentes convergentes o positivas, se utilizan principalmente para corregir la hipermetropía, la presbicia y algunos tipos de astigmatismo.
El tipo de lentes que se estudia más habitualmente son las denominadas como lentes delgadas. Se definen así todas las lentes cuyo grosor es muy reducido en comparación con los radios de curvatura de las superficies que las limitan.
El estudio de este tipo de lentes se puede llevar a cabo principalmente a través de dos ecuaciones: la ecuación de Gauss y la ecuación que permite determinar el aumento de la lente.
La importancia de la ecuación de Gauss de las lentes delgadas radica en la gran cantidad de problemas de óptica básica que permite resolver. Su expresión es la siguiente:
1/f = 1/p +1/q
En donde 1/ f es la potencia de la lente y f es la distancia focal o distancia del centro óptico al foco F. La unidad de medida de la potencia de una lente es la dioptría (D), siendo el valor de 1 D = 1 m-1. Por su parte, p y q son, respectivamente, la distancia a la que ubica un objeto y la distancia a la que se observa su imagen.
Se coloca un cuerpo a 40 centímetros de una lente divergente de -40 centímetros de distancia focal. Calcule la altura de la imagen si la altura del objeto es de 5 cm. Determine también si la imagen es derecha o invertida.
Disponemos de los siguientes datos: h = 5 cm; p = 40 cm; f = -40 cm.
Se sustituyen estos valores en la ecuación de Gauss de las lentes delgadas:
1/f = 1/p +1/q
Y se obtiene:
1/-40 = 1/40 +1/q
De donde q = – 20 cm
A continuación, sustituimos el resultado obtenido anteriormente en la ecuación del aumento de una lente:
M = – q / p = – -20/40= 0,5
Obteniéndose que el valor del aumento es:
M = h’/h = 0,5
Despejando de esta ecuación h’, que es el valor de la altura de la imagen, se llega a:
h’ = h/2 = 2,5 cm.
La altura de la imagen es de 2.5 cm. Además, la imagen es derecha ya que M > 0 y disminuida ya que el valor absoluto de M es inferior a 1.
- Luz (n.d.). En Wikipedia. Recuperado el 11 de abril, 2019, desde es.wikipedia.org.
- Lekner, John (1987). Theory of Reflection, of Electromagnetic and Particle Waves. Springer.
- Light (n.d.). In Wikipedia. Recuperado el 11 de abril, 2019, desde en.wikipedia.org.
- Lente (n.d.). En Wikipedia. Recuperado el 11 de abril, 2019, desde es.wikipedia.org.
- Lens (optics). In Wikipedia. Recuperado el 11 de abril, 2019, desde en.wikipedia.org.
- Hecht, Eugene (2002). Optics (4th ed.). Addison Wesley.
- Tipler, Paul Allen (1994). Física. 3ª Edición. Barcelona: Reverté.
