Número de Froude: cómo se calcula y ejemplos
El número de Froude en hidráulica señala la relación que existe entre las fuerzas inerciales y las fuerzas gravitatorias para un fluido. Por lo tanto, es una manera de designar el siguiente cociente:
Donde NF es la notación para el número de Froude, una cantidad adimensional a la cual se dio este nombre para honrar al ingeniero hidráulico y notable arquitecto naval británico William Froude (1810-1879). Froude y su hijo experimentaron arrastrando láminas planas por el agua para estimar la resistencia que los barcos presentan ante las olas.

En el accionar de las olas causadas por un barco al navegar o la corriente sobre el pilar de un puente, están presentes las fuerzas de inercia y gravedad.
El número de Froude es particularmente importante para caracterizar el flujo de fluido en un canal abierto. Una tubería o canal abierto es un conducto cuya superficie superior está abierta a la atmósfera. En la naturaleza abundan los ejemplos, en forma de ríos y corrientes de agua.
Y en las construcciones hechas por el hombre tenemos:
-Las canaletas y los desagües en calles y edificios para conducir el agua de las lluvias.
-Acequias para el regadío.
-Vertederos y drenajes.
-Canales de enfriamiento para maquinarias industriales.
Todos estos son ejemplos de tuberías abiertas a la atmósfera, en las cuales el número de Froude siempre debe ser tomado en cuenta al momento de caracterizar el flujo.
Índice del artículo
- 1 Cálculo del número de Froude
- 2 Tipos de flujo de acuerdo al número de Froude
- 3 Ejemplo resuelto
- 4 Referencias
El cociente indicado al comienzo, entre las fuerzas de inercia y las de gravedad, toma la forma siguiente, en función de los parámetros del fluido:
La ecuación anterior o bien su raíz cuadrada es el número de Froude:
Tal como se explicó al comienzo, el flujo de agua por canales abiertos a la atmósfera es muy frecuente. Para estos casos, el cálculo del número de Froude se efectúa aplicando la siguiente fórmula:
NF = v /(gyh) ½
Donde yh es la profundidad hidráulica, v es la velocidad media del flujo y g es el valor de la aceleración de la gravedad. A su vez la profundidad hidráulica se calcula de la siguiente forma:
yh = A/T
En esta fórmula, A representa el área de sección transversal neta y T es el ancho de la superficie libre del fluido, la que está expuesta a la atmósfera, en la parte superior del canal o tubería. Es válida para un canal rectangular o bien uno lo bastante ancho y con profundidad constante.
Es importante destacar el hecho de que, puesto que NF es adimensional, entonces el producto gyh debe ser el cuadrado de una velocidad. En efecto, se puede demostrar que:
co2 = gyh
Con co como la velocidad de propagación de una onda superficial, análoga a la velocidad del sonido en un fluido. Por lo tanto el número de Froude también es análogo al número de Mach, muy utilizado para comparar la velocidad de los aviones con la del sonido.
El flujo de fluido en un canal abierto se clasifica en tres regímenes, de acuerdo al valor de NF:
-Cuando NF 1, se tiene un movimiento en régimen lento o subcrítico.
-Si NF = 1 el flujo recibe el nombre de flujo crítico.
-Finalmente si se tiene NF > 1 el movimiento se lleva a cabo en régimen rápido o supercrítico.
El número de Reynolds NR es otra cantidad adimensional importantísima en el análisis del flujo de fluidos, mediante la cual se conoce cuándo el fluido tiene comportamiento laminar y cuándo es turbulento. Estos conceptos son aplicables tanto a flujos en tuberías cerradas como en canales abiertos.
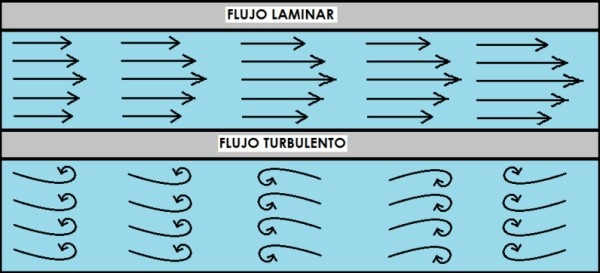
Un flujo es laminar cuando el fluido se mueve suave y ordenadamente en capas que no se mezclan. En cambio el flujo turbulento si se caracteriza por ser caótico y desordenado.
Una forma de averiguar si un flujo de agua es laminar o turbulento es inyectando una corriente de tinta. Si el flujo es laminar, la corriente de tinta fluye por separado de la de agua, pero si se trata de un flujo turbulento la tinta se mezcla y se disipa en el agua rápidamente.
En este sentido, al combinar los efectos del número de Froude con los del número de Reynolds se tiene:
-Laminar subcrítico: NR 500 y NF 1
-Turbulento subcrítico: NR > 2000 y NF 1
-Laminar supercrítico: NR 500 y NF > 1
-Turbulento supercrítico: NR > 2000 y NF > 1
Cuando los flujos ocurren en las regiones de transición es más complicado caracterizarlos, a causa de su inestabilidad.
Un río de 4 m de ancho y 1 m de profundidad tiene un caudal de 3 m3 /s. Determinar si el flujo es subcrítico o supercrítico.
Para encontrar el valor de NF se requiere conocer la velocidad de la corriente del río. El enunciado nos da el caudal, también conocido como rapidez de flujo de volumen, que depende del área de sección transversal y de la velocidad v del flujo. Se calcula así:
Q = A.v
Donde Q es el caudal, A es el área de la sección transversal y v es la velocidad. Suponiendo un área de sección transversal rectangular:
A = ancho x profundidad = 4 m x 1 m = 4 m2
Entonces la velocidad v es:
v = Q/A = 3 m3 /s / 4 m2= 0.75 m/s
La profundidad hidráulica en el caso de la tubería de sección rectangular coincide con la profundidad, por lo tanto, sustituyendo valores en la ecuación de NF, con yh = 1 m y g = 9.8 m/s2 se tiene:
NF = v /(gyh) ½ = 0.75 m/s / (9.8 m/s2 x 1m) ½ = 0.24
Puesto que NF es menor que 1, el flujo tiene un comportamiento subcrítico, esto es, de régimen lento.
- Cimbala, C. 2006. Mecánica de Fluidos, Fundamentos y Aplicaciones. Mc. Graw Hill.
- Franzini, J. 1999. Mecánica de Fluidos con Aplicación es en Ingeniería. Mc. Graw Hill.
- Mott, R. 2006. Mecánica de Fluidos. 4ta. Edición. Pearson Educación.
- White, F. 2004. Mecánica de Fluidos. 5ta Edición. Mc Graw Hill.
- Wikipedia. Número de Froude. Recuperado de: es.wikipedia.org.
