Números complejos: propiedades, ejemplos, operaciones

Los números complejos son el conjunto numérico que abarca a los números reales y a todas las raíces de los polinomios, incluyendo las raíces pares de los números negativos. Estas raíces no existen en el conjunto de los números reales, pero en los números complejos está la solución.

Un número complejo consta de una parte real y otra denominada “imaginaria”. A la parte real se la llama a, por ejemplo, y la parte imaginaria ib, con a y b números reales e “i” como la unidad imaginaria. De esta forma el número complejo toma la forma:

z = a + ib

Ejemplos de números complejos son 2 – 3i, -πi, 1 + (1/2)i. Pero antes de operar con ellos, vamos a ver de dónde se origina la unidad imaginaria i, considerando esta ecuación cuadrática:

x² – 10x + 34 = 0

En la cual a = 1, b = -10 y c = 34.

Cuando se aplica la fórmula resolvente para determinar la solución, nos encontramos con lo siguiente:

¿Cómo determinar el valor de √-36? No existe un número real que elevado al cuadrado resulte una cantidad negativa. Entonces se concluye que esta ecuación no tiene soluciones reales.

Sin embargo, podemos escribir esto:

√-36 = √-6² = √6² (-1) = 6√-1

Si definimos un cierto valor x tal que:

x² = -1

Entonces:

x = ±√-1

Y la ecuación anterior tendría solución. Por ello se definió la unidad imaginaria como:

i = √-1

Y así:

√-36 = 6i

Muchos matemáticos de la antigüedad trabajaron en resolver problemas similares, destacando los renacentistas Girolamo Cardano (1501-1576), Nicolo Fontana (1501-1557) y Raffaele Bombelli (1526-1572).

Años más tarde René Descartes (1596-1650) denominó “imaginarias”  a las cantidades como la √-36 del ejemplo. Por tal motivo a la √-1 se la conoce como la unidad imaginaria.

Índice del artículo

• 1 Propiedades de los números complejos
• 2 Representación de los números complejos
  • 2.1 – Forma binómica
  • 2.2 – Forma polar
• 3 Ejemplos de números complejos
• 4 ¿Para qué sirven?
• 5 Operaciones con números complejos
  • 5.1 – Ejemplo 1
  • 5.2 – Ejemplo 2
• 6 Aplicación
• 7 Referencias

Propiedades de los números complejos

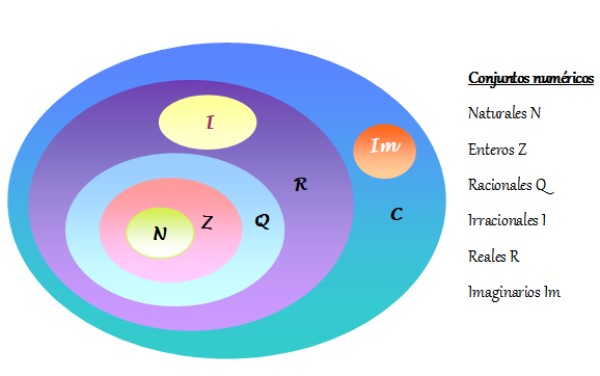
-El conjunto de los números complejos se denota como C e incluye a los números reales R y a los números imaginarios Im. Los conjuntos numéricos se representan en un diagrama de Venn, como se muestra en la siguiente figura:

-Todo número complejo consta de una parte real y otra parte imaginaria.

-Cuando la parte imaginaria de un número complejo es 0, se trata de un número real puro.

-Si la parte real de un número complejo es 0, entonces el número es imaginario puro.

-Dos números complejos son iguales si sus respectivas parte real y parte imaginaria son las mismas.

-Con los números complejos se realizan las operaciones conocidas de sumas, resta, multiplicación, producto y potenciación, dando como resultado otro número complejo.

Representación de los números complejos

Los números complejos se pueden representar de diversas maneras. He aquí las principales:

– Forma binómica

Es la forma dada al principio, donde z es el número complejo, a es la parte real, b es la parte imaginaria e i es la unidad imaginaria:

z = a + ib

O también:

z = x + iy

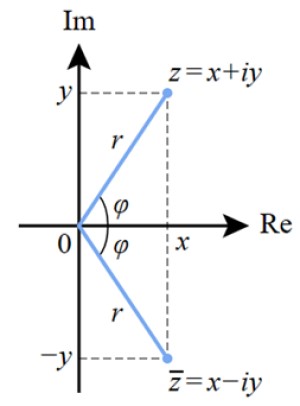
Una forma de representar gráficamente al número complejo es a través del plano complejo que se muestra en esta figura. El eje imaginario Im es vertical, mientras que el eje real es horizontal y se denota como Re.

El número complejo z se representa en este plano como un punto de coordenadas (x,y) o (a,b), tal como se hace con los puntos del plano real.

La distancia desde el origen al punto z es el módulo del número complejo, denotado como r, mientras que φ es el ángulo que forma r con el eje real.

Esta representación guarda estrecha relación con la de los vectores en el plano real. El valor de r corresponde al módulo del número complejo.

– Forma polar

La forma polar consiste en expresar el número complejo dando los valores de r y de φ. Si nos fijamos en la figura, el valor de r corresponde a la hipotenusa de un triángulo rectángulo. Los catetos valen a y b, o bien x y y.

De la forma binómica o binomial, podemos pasar a la forma polar mediante:

r = √x²+y²

El ángulo φ es el que forma el segmento r con el eje horizontal o eje imaginario. Se le conoce como argumento del número complejo. De esta manera:

φ = arctg (y/x)

El argumento tiene infinitos valores, tomando en cuenta que cada vez que se gira una vuelta, la cual vale 2π radianes, r vuelve a ocupar la misma posición. De esta forma en general, el argumento de z, denotado Arg (z), se expresa así:

Arg (z) = φ + 2kπ

Donde k es entero y sirve para indicar la cantidad de vueltas giradas: 2, 3, 4…. El signo señala el sentido del giro, si se hace horario o antihorario.

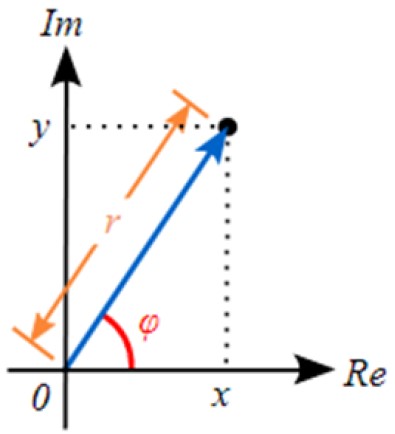
Y si queremos pasar de la forma polar a la forma binomial, empleamos las razones trigonométricas. De la figura anterior podemos ver que:

x = r cos φ

y = r sen φ

De esta forma z = r (cos φ+i sen φ)

Que se abrevia así:

z = r cis φ

Ejemplos de números complejos

Los siguientes números complejos están dados en forma binomial:

a) 3 + i

b) 4

d) -6i

Y estos en forma de par ordenado:

a) (-5, -3)

b) (0, 9)

c) (7,0)

Por último, este grupo viene dado en forma polar o trigonométrica:

a) √2 cis 45º

b) √3 cis 30º

c) 2 cis 315º

¿Para qué sirven?

La utilidad de los números complejos va más allá de la resolución de la ecuación de segundo grado mostrada al comienzo, ya que son imprescindibles en el campo de la ingeniería y de la física, sobre todo en:

-El estudio de las ondas electromagnéticas

-Análisis de la corriente y el voltaje alternos

-La modelización de toda clase de señales

-Teoría de la relatividad, donde el tiempo se asume como una magnitud imaginaria.

Operaciones con números complejos

Con los números complejos podemos realizar todas las operaciones que se hacen con los reales. Algunas son más fáciles de hacer si los números vienen en forma binómica, como por ejemplo la suma y la resta. En cambio, la multiplicación y la división son más simples si se llevan a cabo con la forma polar.

Veamos algunos ejemplos:

– Ejemplo 1

Sumar z₁ = 2 + 5i y z₂ = -3 -8i

Solución

Se suman las partes reales por separado de las partes imaginarias:

z₁ + z₂ = (2 + 5i) + (-3 -8i) = -1 -3i

– Ejemplo 2

Multiplicar z₁ = 4 cis 45º y z₂ = 5 cis 120º

Solución

Se puede demostrar que el producto de dos números complejos en forma polar o trigonométrica viene dado por:

z₁ . z₂ = r₁.r₂ cis (φ₁ + φ₂)

De acuerdo a esto:

z₁ . z₂ = (4×5) cis (45 + 120) = 20 cis 165º

Aplicación

Una aplicación sencilla de los números complejos es hallar todas las raíces de una ecuación polinómica como la que se muestra al principio del artículo.

En el caso de la ecuación  x² – 10x + 34 = 0, al aplicar la fórmula resolvente se obtiene:

Por lo tanto las soluciones son:

x₁ = 5 + 3i

x₂ = 5 – 3i

Referencias

1. Earl, R. Complex numbers. Recuperado de: maths.ox.ac.uk.
2. Figuera, J. 2000. Matemática 1ro. Diversificado. ediciones CO-BO.
3. Hoffmann, J. 2005. Selección de temas de Matemática. Publicaciones Monfort.
4. Jiménez, R. 2008. Álgebra. Prentice Hall.
5. Wikipedia. Complex numbers. Recuperado de: en.wikipedia.org