Muestreo por cuotas: método, ventajas, desventajas, ejemplos
El muestreo por cuotas es una forma no probabilística de tomar los datos de una muestra asignando cuotas por estratos. Las cuotas deben ser proporcionales a la fracción que representa dicho estrato respecto a la población total y la suma de las cuotas debe ser igual al tamaño de la muestra.
El investigador es quien decide cuáles serán los grupos o los estratos, por ejemplo puede dividir una población en hombres y mujeres. Otro ejemplo de estratos son rangos de edad, por ejemplo de 18 a 25, de 26 a 40 y de 40 en adelante, que pueden etiquetarse así: jóvenes, adultos y mayores.

Es muy conveniente conocer previamente qué porcentaje de la población total representa cada estrato. Luego se elige un tamaño de muestra que sea estadísticamente significativo, y se asignan cuotas proporcionales al porcentaje de cada estrato respecto a la población total. La suma de las cuotas por estrato debe ser igual al tamaño total de la muestra.
Finalmente se procede a tomar los datos de las cuotas asignadas a cada estrato, eligiendo los primeros elementos que completan la cuota.
Es precisamente a causa de esta forma no-aleatoria de elegir los elementos, que este método de muestreo se considera no probabilístico.
Índice del artículo
- 1 Pasos para realizar un muestreo por cuotas
- 2 Caso práctico
- 3 Aplicabilidad, ventajas y desventajas
- 4 Ejemplo sencillo de aplicación
- 5 Ejercicio propuesto
- 6 Referencias
Segmentar la población total en estratos o grupos con alguna característica común. Dicha característica será decidida previamente por el investigador estadístico que conduce el estudio.
Determinar qué porcentaje respecto a la población total representa cada uno de los estratos o grupos elegidos en el paso anterior.
Estimar un tamaño de muestra estadísticamente significativo, de acuerdo a los criterios y metodologías propios de la ciencia estadística.
Calcular el número de elementos o cuotas por cada estrato, de modo que sean proporcionales al porcentaje que representa cada uno de ellos respecto de la población total y del tamaño total de la muestra.
Tomar la data de los elementos en cada estrato hasta completar la cuota correspondiente a cada estrato.
Supongamos que se desea conocer el nivel de satisfacción con respecto al servicio de metro en una ciudad. Estudios previos sobre una población de 2000 personas determinaron que el 50% de los usuarios son jóvenes entre 16 y 21 años, el 40% son adultos entre 21 y 55 años y solo un 10% de los usuarios son mayores de más de 55 años.
Aprovechando los resultados de este estudio se segmenta o estratifica de acuerdo a la edad de los usuarios:
-Jóvenes: 50%
-Adultos: 40%
-Mayores: 10%
Como se dispone de un presupuesto limitado, el estudio ha de aplicarse a una muestra pequeña, pero que sea estadísticamente significativa. Se elige un tamaño de muestra de 200, es decir la encuesta sobre nivel de satisfacción se aplicará a 200 personas en total.
Falta ahora determinar la cuota o número de encuestas por cada segmento o estrato, el cual debe ser proporcional al tamaño de la muestra y al porcentaje por estrato.
Cuota por estrato
La cuota de número de encuestas por estrato queda así:
Jóvenes: 200 * 50% = 200 * (50/100) = 100 encuestas
Adultos: 200 * 40% = 200 * (40/100) = 80 encuestas
Mayores: 200 * 10% = 200 * (10/100) = 20 encuestas
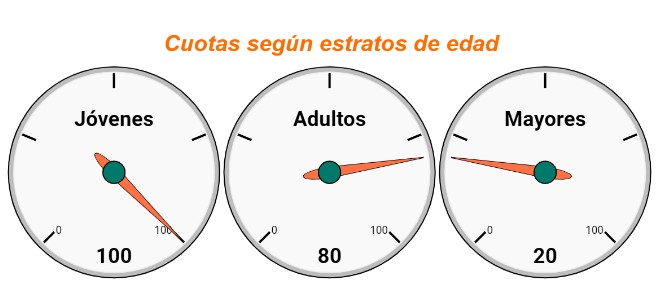
Note que la suma de las cuotas tiene que ser igual al tamaño de la muestra, es decir igual al número total de encuestas que se aplicarán. Luego se pasan las encuestas hasta cumplir las cuotas por cada estrato.
Es importante destacar que este método es mucho mejor que tomar todas las encuestas y pasarlas a las primeras 200 personas que aparezcan, porque de acuerdo a los datos previos, es muy probable que el estrato minoritario quede fuera del estudio.
Para que el método sea aplicable se requiere de un criterio para la formación de los estratos, el cual depende del objetivo del estudio.
El muestreo por cuotas es adecuado cuando se desea conocer las preferencias, diferencias o características por sectores para dirigir campañas específicas según el estrato o segmento.
También resulta útil su uso cuando por algún motivo interesa conocer las características o intereses de sectores minoritarios, o cuando no se quieren dejar fuera del estudio.
Para que sea aplicable debe conocerse el peso o significancia de cada estrato respecto de la población total. Es muy importante que este conocimiento sea fidedigno, de lo contrario se obtendrán resultados errados.
-Disminuye los tiempos del estudio, porque las cuotas por estrato suelen ser pequeñas
-Simplifica el análisis de los datos.
-Minimiza los costos porque el estudio se aplica a muestras pequeñas pero bien representativas de la población total.
-Como los estratos son definidos a priori, es posible que ciertos sectores de la población queden fuera del estudio.
-Al establecer un número limitado de estratos, es posible que se esté perdiendo detalle en el estudio.
-Al obviar o incorporar como parte de otro algún estrato puede tenerse conclusiones equivocadas en el estudio.
-Imposibilita la estimación del error máximo de muestreo.
Se desea hacer un estudio estadístico sobre el nivel de ansiedad en una población de 2000 personas.
El investigador que dirige la investigación intuye que deben encontrarse diferencias en los resultados dependiendo de la edad y del sexo. Por ello decide formar tres estratos de edad denotados así: Primera_Edad, Segunda_Edad y Tercera_Edad. Respecto al segmento sexo se definen los dos tipos usuales: Masculino y Femenino.
Se define Primera_Edad, la comprendida entre 18 y 25 años, Segunda_Edad la comprendida entre 26 y 50 años y finalmente Tercera_Edad la comprendida entre 50 y 80 años.
Analizando los datos de la población total se tiene que:
El 45% de la población pertenece a la Primera_Edad.
El 40% está en la Segunda_Edad.
Por último solo el 15% de la población en estudio pertenece a la Tercera_Edad.
Usando una metodología adecuada, que no se detalla aquí, se determina que una muestra de 300 personas es estadísticamente significativa.
El próximo paso será entonces encontrar las cuotas correspondientes por el segmento Edad, lo cual se realiza de la siguiente manera:
Primera_Edad: 300 * 45% = 300 * 45 / 100 = 135
Segunda_Edad: 300 * 40% = 300 * 40 / 100 = 120
Tercera_Edad: 300 * 15% = 300 * 15 / 100 = 45
Se verifica que la suma de las cuotas da el tamaño total de la muestra.
Hasta el momento no se ha tomado en cuenta el segmento sexo de la población, de este segmento ya se han definido dos estratos: Femenino y Masculino. De nuevo hay que analizar los datos de la población total, los cuales arrojan la siguiente información:
-El 60% de la población total son de sexo Femenino.
-Mientras, un 40% de la población a ser estudiada pertenece al sexo Masculino.
Es importante señalar que los porcentajes anteriores en cuanto a la distribución de la población según el sexo, no toman en cuenta la edad.
En vista que no se dispone de más información, se hará la suposición que estas proporciones en cuanto a sexo están igualmente distribuidas en los 3 estratos de Edad que se han definido para este estudio. Con estas consideraciones pasamos ahora a establecer las cuotas por Edad y Sexo, lo cual significa que ahora se tendrán 6 sub-estratos:
S1 = Primera_Edad y Femenino: 135 * 60% = 135 * 60 /100 = 81
S2 = Primera_Edad y Masculino: 135 * 40% = 135 * 40 /100 = 54
S3 = Segunda_Edad y Femenino: 120 * 60% = 120 * 60 /100 = 72
S4 = Segunda_Edad y Masculino: 120 * 40% = 120 * 40 /100 = 48
S5 = Tercera_Edad y Femenino: 45 * 60% = 45 * 60 /100 = 27
S6 = Tercera_Edad y Masculino: 45 *40% = 45 * 40 /100 = 18
Aplicación de encuestas y estudio de los resultados
Una vez establecido los seis (6) segmentos y sus correspondientes cuotas se procede a preparar 300 encuestas que se aplicarán según las cuotas ya calculadas.
Las encuestas se aplicarán de la siguiente manera, se toman 81 encuestas y se entrevista a las primeras 81 personas que estén en el segmento S1. Luego se hace de igual manera con los restantes cinco segmentos.
La secuencia de estudio es como sigue:
-Analizar los resultados de la encuesta, que luego se discuten, analizando los resultados por segmento.
-Hacer las comparaciones entre los resultados por segmento.
-Finalmente elaborar hipótesis que expliquen las causas de dichos resultados.
En nuestro ejemplo en el que aplicamos el muestreo por cuotas, lo primero que se hace es establecer las cuotas para luego realizar el estudio. Claro que estas cuotas no son del todo caprichosas, porque se han basado en información estadística previa sobre la población total.
En caso de no poseer información previa sobre la población en estudio, es preferible llevar el procedimiento a la inversa, es decir, definir primero el tamaño de la muestra y una vez establecido el tamaño de la muestra, proceder a la aplicación de la encuesta en forma aleatoria.
Una forma de asegurar la aleatoriedad sería usar un generador de números aleatorios y encuestar a los empleados cuyo número de empleado coincida con el del generador aleatorio.
Una vez se tengan los datos, y como el objetivo del estudio es ver los niveles de ansiedad según los estratos de edad y sexo, se procede a separar la data según las seis categorías que habíamos definido previamente. Pero sin establecer ninguna cuota previa.
Es por esta razón que el método de muestreo aleatorio estratificado se considera un método probabilístico. Mientras que el muestreo por cuotas previamente establecidas no.
Sin embargo, si las cuotas se establecen con información basada en las estadísticas de la población, entonces puede decirse que el método de muestreo por cuotas es aproximadamente probabilístico.
Se propone el siguiente ejercicio:
En un colegio de educación secundaria se quiere hacer una encuesta sobre la preferencia entre estudiar ciencias o estudiar humanidades.
Suponga que el colegio tiene en total 1000 estudiantes agrupados en cinco niveles según el año de estudio. Se sabe que hay 350 estudiantes en primer año, 300 en segundo, 200 en tercero, 100 en cuarto y por último 50 en quinto año. Se sabe también que el 55% de los estudiantes del colegio son chicos y 45% son chicas.
Determine los estratos y las cuotas por estrato, para saber el número de encuestas a aplicar atendiendo los segmentos año de estudio y sexo. Suponga adicionalmente que la muestra será de un 10% de la población total de estudiantes.
- Berenson, M. 1985.Estadística para Administración y Economía, Conceptos y Aplicaciones. Editorial Interamericana.
- Estadística. Muestreo por cuotas. Recuperado de: enciclopediaeconomica.com.
- Estadística. Muestreo. Recuperado de: estadistica.mat.uson.mx.
- Explorable. Muestreo por cuotas. Recuperado de: explorable.com.
- Moore, D. 2005. Estadística Básica Aplicada. 2da. Edición.
- Netquest. Muestreo probabilístico: muestreo estratificado. Recuperado de: netquest.com.
- Wikipedia. Statistical sampling. Recuperado de: en.wikipedia.org
