Divisores de 120: qué son, cómo se calculan y ejercicios resueltos

Los divisores de 120 son todos aquellos números que lo dividen exactamente. Dichos números son los siguientes:

Divisores de 120 = {1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120}

También los opuestos a este conjunto de números, es decir, los negativos, son divisores de 120, puesto que la división resulta exacta. El 120 tiene 16 divisores enteros positivos y otros tantos negativos.

Hay varias maneras de hallar los divisores de un número. Si este no es muy grande, se pueden usar las tablas de multiplicar (para números menores que 100) y verificar en cuáles tablas aparece el número en cuestión. Por ejemplo, el 12 aparece en las tablas del 2, 3, 4 y 6, y estos son sus divisores, junto con el 1 y el mismo 12.

También se puede descomponer el número en sus factores primos, aplicar las reglas de divisibilidad y multiplicar los factores. Pero hay que tener cuidado de no pasar ningún divisor por alto.

Como el 120 es mayor que 100, no se encuentra directamente en las tablas de multiplicar, sin embargo, no es demasiado laborioso hallar sus 16. Enseguida se muestra un procedimiento válido para todos los números, mediante el uso de tablas muy sencillas.

¿Cuántos divisores tiene 120?

En primer lugar, se averigua el número de divisores de 120. Existe una fórmula que permite saber cuántos tiene, aunque no dice cuáles son.

Los números compuestos, como el 120, se pueden expresar como el producto de números primos, o potencias de estos. Llamando N a un número compuesto cualquiera:

N = aⁿ ∙ b^m ∙ c^p … r^k

Los números a, b, c…r son números primos, y los valores de n, m, p, …k, las respectivas potencias. La descomposición en factores primos de 120 es la siguiente:

120|2
60|2
30|2
15|3
5|5
1|1

De esta forma, 120 es el producto de los factores:

120 = 2³ ∙ 3 ∙ 5

Fórmula para calcular el número de divisores de N

Número de divisores = (n +1) × (m+1) × (p +1) …× (k+1)

Ahora se aplica la fórmula a 120. De la descomposición en factores se tiene que:

n = 3 (Es la potencia del 2)

m = 1 (El 3 está elevado a la 1: 3¹ = 3)

p = 1 (El 5 también aparece elevado a la 1)

Con estos valores:

Número de divisores de 120 = (3 +1) × (1+1) × (1 +1) = 4 × 2 × 2 = 16

Este resultado coincide con la figura del comienzo: el 120 tiene 16 divisores. Además, ya se sabe que el 2, el 3 y el 5 son divisores de 120, así como el 10, ya que cualquier número terminado en 0 es divisible por 10. Enseguida se muestra el procedimiento para encontrarlos a todos.

Cálculo de los divisores de 120

Se hace con ayuda de los factores calculados en la sección anterior. Allí se vió que el 2 es un factor primo con exponente 3, y el 3 es otro factor primo, con exponente 1. Con esta información se construye la siguiente tabla:

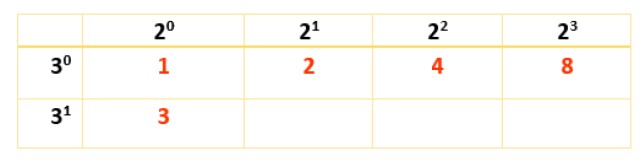
Nótese que las potencias de 2 comienzan en 2⁰ y terminan en 2³, que es el factor que surge al descomponer 120. Recuérdese que 2⁰ y 3⁰ ambos son igual a 1 (cualquier número elevado a 0 es 1). Para el factor 3, se comienza en 3⁰ hasta 3¹, ya que 3¹ = 3.

Seguidamente, se completa la tabla con el producto de los números en rojo, como se muestra acá:

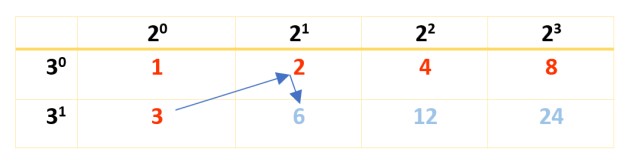
Todos los números en rojo y en azul son divisores de 120, pero apenas hay 8. Para hallar los restantes, se contruye una nueva tabla, se escriben los divisores ya obtenidos en la primera fila y el factor que falta por tomar en cuenta: el 5, con sus potencias en la primera columna, a la izquierda, así:

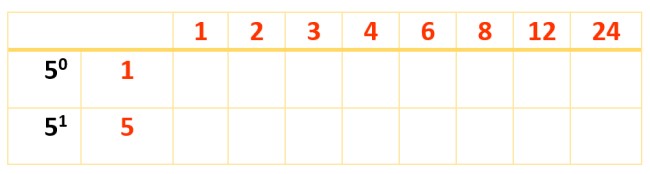
Ahora, se completa la tabla con los productos de los números en rojo, como se hizo con la primera tabla:

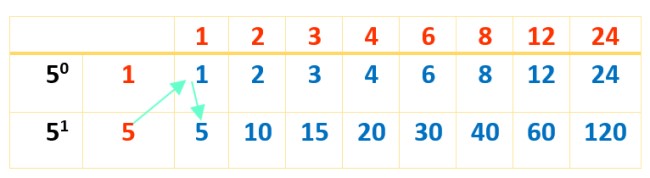
Y por fin aparecen los 16 divisores de 120 en color azul. Las tablas son una excelente ayuda para que que las operaciones se hagan en orden y así ningún divisor de 120 quede por fuera.

Ejercicios resueltos

El procedimiento para hallar todos los divisores de un número se resume así:

1. Descomponer el número en factores primos.
2. Calcular la cantidad de divisores con la fórmula.
3. Construir la o las tablas necesarias para encontrar los divisores. Si el número tiene dos factores, basta con una tabla, si tiene tres factores, hay que hacer dos tablas, como en el caso de 120.

Ejercicio 1

Hallar todos los divisores de 288.

Solución

Se descompone 288 en factores primos:

288|2
144|2
72|2
36|2
18|2
9|3
3|3
1|1

El 288 se escribe así:

288 = 2⁵ ∙3²

De inmediato se encuentra el número de divisores de 288 mediante:

Número de divisores = (n +1) × (m+1) × (p +1) …× (k+1)

De la descomposición en factores primos se advierte que n = 5 y m = 2, entonces:

Divisores de 288 = (5 +1) × (2+1) = 6 × 3 = 18

Hay 18 divisores y como solamente hay dos factores, es suficiente con una sola tabla:

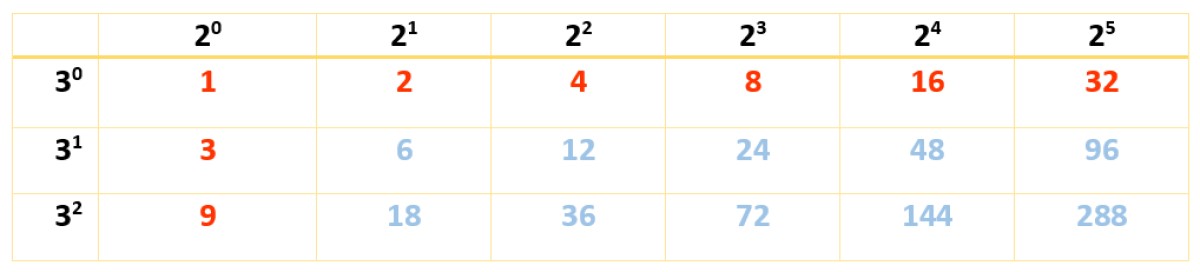
Los divisores de 288 son los números en rojo y en azul:

Div (288) = {1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288}

Se pueden comprobar rápidamente con ayuda de una calculadora.

Ejercicio 2

Hallar los divisores de 350

Solución

Se descompone el 350:

350|2
175|5
35|5
7|7
1|1

El 350 se puede escribir como producto de tres factores:

350 = 2 ∙5²∙7

El siguiente paso es calcular cuántos divisores tiene, a través de la fórmula:

Número de divisores = (n +1) × (m+1) × (p +1) …× (k+1)

Con n = 1, m = 2, p = 1

Divisores de 288 = (1 +1) × (2+1) ×(1 +1) = 2 × 3 × 2= 12

Como 350 requiere de tres factores, hay que hacer dos tablas. La primera se hace con 2 y 5², pero también puede hacerse con 2 y 7, o con 7 y 5², según la preferencia, ya que de todas las formas, el resultado final es el mismo:

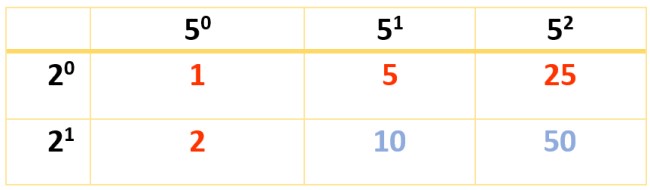
Se obtienen 6 divisores. Los demás aparecen con ayuda de esta otra tabla:

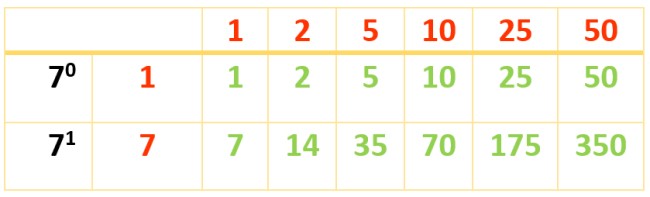
Los divisores de 350 son:

Div (350) = {1, 2, 5, 7, 10, 14, 25, 35, 50, 70, 175, 350}