Coordenadas esféricas: ejemplos y ejercicios resueltos
Las coordenadas esféricas son un sistema de ubicación de puntos en el espacio tridimensional que consta de una coordenada radial y dos coordenadas angulares denominadas coordenada polar y coordenada azimutal.
En la figura 1, que vemos a continuación, se muestra las coordenadas esféricas (r, θ, φ) de un punto M. Estas coordenadas están referidas a un sistema ortogonal de ejes cartesianos X, Y, Z de origen O.

En este caso, la coordenada r del punto M es la distancia de ese punto al origen O. La coordenada polar θ representa el ángulo entre el semieje positivo Z y el radio vector OM. Mientras que la coordenada azimutal φ es el ángulo entre el semieje positivo X y el radio vector OM’, siendo M’ la proyección ortogonal de M sobre el plano XY.
La coordenada radial r solo toma valores positivos, pero si un punto está ubicado en el origen entonces r=0. La coordenada polar θ toma como valor mínimo 0º para puntos ubicados sobre el semieje positivo Z y valor máximo 180º para los puntos está ubicado en el semieje negativo Z. Por último, la coordenada azimutal φ toma como valor mínimo 0º y cota máxima de 360º.
0 ≤ r ∞
0 ≤ θ ≤ 180º
0 ≤ φ 360º
Índice del artículo
- 1 Cambio de coordenadas
- 2 Relación con las coordenadas geográficas
- 3 Ejemplos
- 4 Ejercicios
- 5 Referencias
A continuación se darán las fórmulas que permiten obtener las coordenadas cartesianas (x, y, z) de un punto M suponiendo conocidas las coordenadas esféricas del mismo (r, θ, φ) punto:
x = r Sen(θ) Cos(φ)
y = r Sen(θ) Sen(φ)
z = r Cos(θ)
De igual manera, es útil hallar las relaciones para pasar de las coordenadas cartesianas (x, y, z) de un punto dado a las coordenadas esféricas de dicho punto:
r = √( x^2 + y^2 + z^2 )
θ = Arctan( √( x^2 + y^2) / z )
φ = Arctan( y / x )
A partir de las coordenadas esféricas se define una base ortonormal de vectores base, los cuales se denotan por Ur, Uθ, Uφ. En la figura 1 se muestran estos tres vectores unitarios, los cuales tienen las siguientes características:
– Ur es el vector unitario tangente a la recta radial θ = ctte y φ = ctte;
– Uθ es el vector unitario tangente al arco φ = ctte y r = ctte;
– Uφ es el vector unitario tangente al arco r = ctte y θ = ctte.
El vector posición de un punto en el espacio en coordenadas esféricas se escribe así:
r = r Ur
Pero una variación o desplazamiento infinitesimal de un punto en el espacio tridimensional, en estas coordenadas está expresado mediante la siguiente relación vectorial:
dr = dr Ur + r dθ Uθ + r Sen(θ) dφ Uφ
Por último, un volumen infinitesimal dV en las coordenadas esféricas se escribe así:
dV = r^2 Sen(θ) dr dθ dφ
Estas relaciones son de gran utilidad para el cálculo de integrales de línea y de volumen en las situaciones físicas que tengan simetría esférica.
Se entiende por coordenadas geográficas las que sirven para ubicar lugares en la superficie terrestre. Este sistema usa las coordenadas de la latitud y la longitud para ubicar la posición sobre la superficie de la Tierra.
En el sistema de coordenadas geográficas, la superficie terrestre se supone esférica de radio Rt, aun cuando se sabe que es achatada en los polos, y se considera un conjunto de líneas imaginarias denominadas paralelos y meridianos.
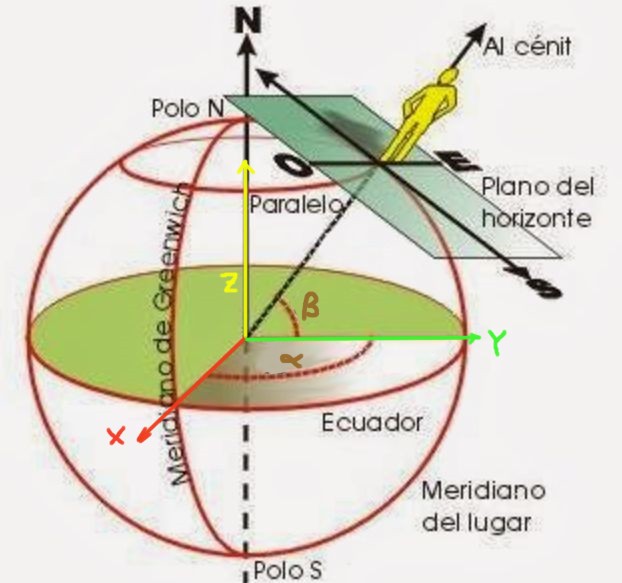
La latitud β es un ángulo formado por un radio que parte del centro de la Tierra hasta el punto que se quiere posicionar. Se mide a partir del plano ecuatorial, tal como se muestra en la figura 2. Por otra parte, la longitud α es el ángulo que el meridiano del punto que se está ubicando forma respecto del meridiano cero (conocido como meridiano de Greenwich).
La latitud puede ser norte o latitud sur ,dependiendo si el lugar que se está ubicando está en el hemisferio norte o en el hemisferio sur. Similarmente, la longitud puede ser oeste o este dependiendo de si la ubicación está al oeste o el este del meridiano cero.
Para obtener estas fórmulas lo primero es establecer un sistema de coordenadas. Se elige el plano XY coincidiendo con el plano ecuatorial, siendo el semieje positivo X el que va del centro de la Tierra y pasando por el meridiano cero. A su vez, el eje Y pasa por el meridiano 90º E. La superficie terrestre tiene radio Rt.
Con este sistema de coordenadas las transformaciones de geográficas a esférica quedan así:
αEβN → (Rt, θ=90º-β, φ=α)
αOβN → (Rt, θ=90º-β, φ=360º-α)
αEβS → (Rt, θ=90º+β, φ=α)
αOβS → (Rt, θ=90º+β, φ=360º-α)
Las coordenadas geográficas de Palma de Mallorca (España) son:
Longitud Este 38,847º y Latitud Norte 39,570º. Para determinar las coordenadas esféricas correspondientes a Palma de Mallorca se aplica la primera de las fórmulas de las fórmulas de la sección previa:
38,847ºE39,570ºN → (r=6371 km, θ=90º-39,570º, φ=38,847º)
Entonces las coordenadas esféricas son:
Palma de Mallorca:(r=6371 km, θ=50,43º, φ=38,85º)
En la respuesta anterior se ha tomado r igual al radio promedio de la Tierra.
Sabiendo que las islas Malvinas (Falkland) tienen coordenadas geográficas 59ºO 51,75ºS, determinar las coordenadas polares correspondientes. Recordar que el eje X va del centro de la Tierra al meridiano 0º y sobre el plano ecuatorial; el eje Y también en el plano ecuatorial y pasando por el meridiano 90º Oeste; por último el eje Z en el eje de rotación terrestre en sentido Sur-Norte.
Para hallar entonces las coordenadas esféricas correspondientes usamos las fórmulas presentadas en la sección anterior:
59ºO 51,75ºS → (r=6371 km, θ=90º+51,75º, φ=360º-59º) es decir
Malvinas:(r=6371 km, θ=141,75º, φ=301º)
Hallar las coordenadas cartesianas de Palma de Mallorca en el sistema de referencia cartesiano XYZ mostrado en la figura 2.
Solución: Previamente, en el ejemplo 1 se obtuvo las coordenadas esféricas partiendo de las coordenadas geográficas de Palma de Mallorca. De modo que pueden usarse las fórmulas presentadas más arriba para pasar de esféricas a cartesianas:
x = 6371 km Sen(50,43º) Cos(38,85º)
y = 6371 km Sen(50,43º) Sen(38,85º)
z = 6371 km Cos(50,43º)
Realizando los cálculos correspondientes se tiene:
Palma de Mallorca: (x=3825 km, y=3081 km, z=4059)
Hallar las coordenadas cartesianas de las islas Malvinas en el sistema de referencia cartesiano XYZ mostrado en la figura 2.
Solución: Previamente en el ejemplo 2 se obtuvo las coordenadas esféricas partiendo de las coordenadas geográficas de las islas Malvinas. De modo que pueden usarse las fórmulas presentadas más arriba para pasar de esféricas a cartesianas:
x = 6371 km Sen(141,75º) Cos(301º)
y = 6371 km Sen(141,75º) Sen(301º)
z = 6371 km Cos(141,75º)
Realizando los cálculos correspondientes se obtiene:
Islas Malvinas: (x=2031 km, y=-3381 km, z=-5003)
- Arfken G and Weber H. (2012). Mathematical methods for physicists. A comprehensive guide. 7th edition. Academic Press. ISBN 978-0-12-384654-9
- Cálculo cc. Problemas resueltos de coordenadas cilíndricas y esféricas. Recuperado de: calculo.cc
- Taller astronomía. Latitud y longitud. Recuperado de: tarifamates.blogspot.com/
- Weisstein, Eric W. “Spherical Coordinates.” From MathWorld-A Wolfram Web. Recuperado de: mathworld.wolfram.com
- wikipedia. Spherical coordinate system. Recuperado de: en.wikipedia.com
- wikipedia. Vector fields in cylindrical and spherical coordinates. Recuperado de: en.wikipedia.com
