Funciones trigonométricas: básicas, en el plano cartesiano, ejemplos, ejercicio
Las funciones trigonométricas de variable real hacen corresponder a un ángulo cualquiera (expresado en en radianes), una razón trigonométrica, que puede ser seno, coseno, tangente, cotangente, secante y cosecante.
De esta manera tenemos las seis funciones trigonométricas: seno, coseno, tangente, cosecante, secante y cotangente.
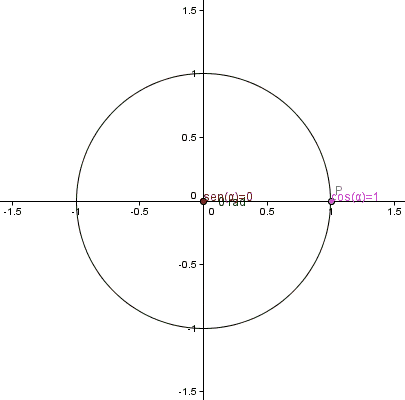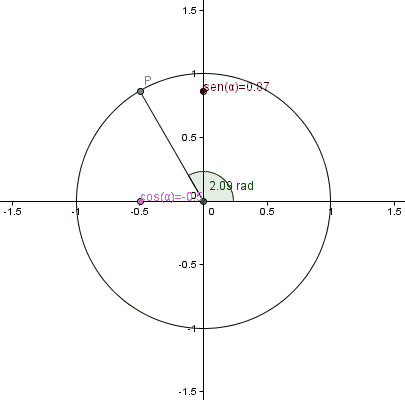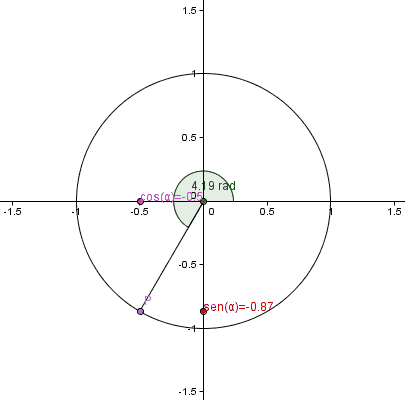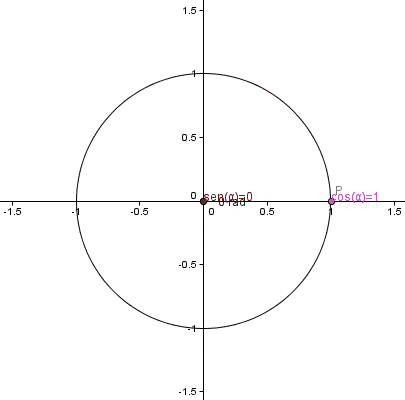
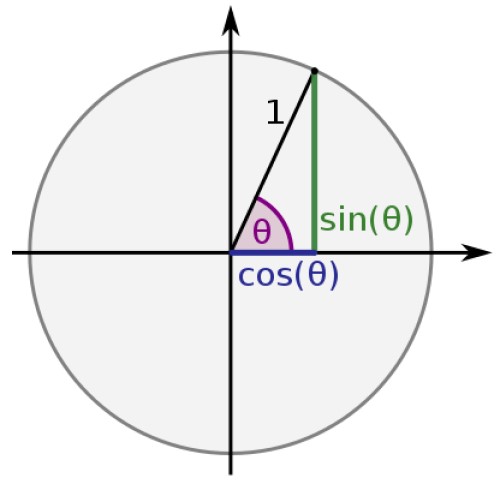
Las funciones trigonométricas para ángulos comprendidos entre 0 y 2π se definen con la ayuda de la circunferencia unitaria, de radio 1 y cuyo centro coincide con el del origen del sistema de coordenadas cartesianas: el punto (0,0).
Podemos ubicar cualquier punto P de coordenadas (x,y) sobre esta circunferencia.
El segmento que une al origen con P, junto a los respectivos segmentos que unen a las proyecciones de P sobre los ejes coordenados, conforman un triángulo rectángulo, cuyas razones trigonométricas son conocidas como los cocientes entre los lados del triángulo. Así:
- sen θ = cateto opuesto /hipotenusa
- cos θ = cateto adyacente /hipotenusa
- tg θ = cateto opuesto /cateto adyacente
Y ahora las razones que son el inverso de las anteriores:
- sec θ = hipotenusa /cateto adyacente
- cosec θ = hipotenusa /cateto opuesto
- ctg θ = cateto adyacente /cateto opuesto
En el círculo unitario la hipotenusa de cualquier triángulo es igual a 1 y los catetos valen x e y, entonces:
sen θ = y
cos θ = x
De esta forma, las funciones seno y coseno siempre adquieren valores comprendidos entre -1 y 1, mientras que las restantes:
tg θ = y/x
cosec θ = 1/y
sec θ = 1/x
No están definidas cuando x o y valen 0.
Índice del artículo
Como veremos a continuación, las funciones trigonométricas se caracterizan por ser periódicas. Por ello no son biyectivas, salvo en un dominio restringido.
Comenzando en el círculo trigonométrico en el punto P (1,0), el ángulo es 0 radianes. Después el radio gira en sentido antihorario y la función sen x va creciendo paulatinamente hasta llegar a π/2 radianes (90º), equivalente a 1.571 radianes aproximadamente.
Allí alcanza el valor y = 1 y después va disminuyendo hasta llegar a cero en π radianes (180°). Posteriormente disminuye aún más, ya que el valor se hace negativo hasta alcanzar −1 cuando el ángulo es 3π/2 radianes (270°).
Por último, aumenta nuevamente hasta regresar a cero en 360°, donde todo comienza de nuevo. Esto hace de y = sen x una función periódica de período 2π, por ello la función seno no es biyectiva.
Además, la gráfica es simétrica con respecto al punto (0,0), por lo tanto la función es impar.
A continuación la gráfica de y = sen x:
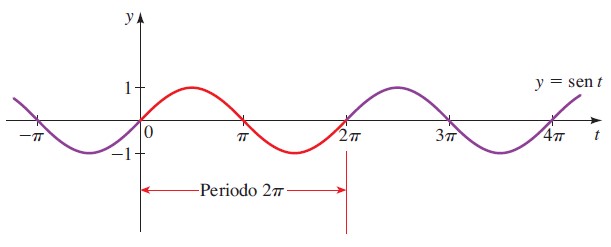
La sección en color rojo es el primer período. Los ángulos negativos también se consideran, ya que el radio del círculo trigonométrico puede girar en sentido horario.
Dominio de sen x = Todos los reales.
Rango o recorrido de sen x = [-1,1]
En el punto P (1,0) la función coseno vale 1 y a partir de allí disminuye, llegando a 0 cuando el ángulo es π/2. Sigue disminuyendo y toma valores negativos, hasta llegar a -1 en el ángulo π.
Entonces comienza a aumentar paulatinamente hasta llegar a 0 en 3π/2 y vuelve a tomar el valor 1 cuando el radio ha dado una vuelta completa. A partir de allí el ciclo se repite, ya que cos x es periódica y además es par (simétrica alrededor del eje vertical).
La forma de la función coseno es la misma que la de la función seno, salvo que están desplazadas π/2 una respecto a la otra.
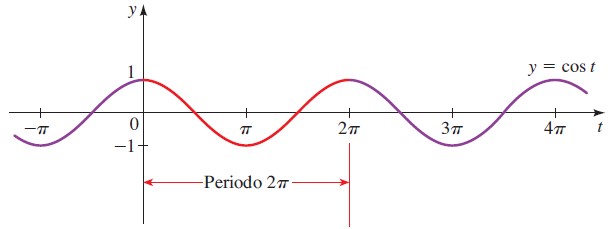
Dominio de cos x = Todos los reales.
Rango o recorrido de cos x = [-1,1]
Las funciones tg x, ctg x, sec x y cosec x son discontinuas, ya que son cocientes entre seno y coseno, o bien las inversas. Como estas valen 0 en algunos ángulos, cuando aparecen en el denominador hacen que la función sea discontinua.
Y puesto que seno y coseno son funciones periódicas, las funciones tg x, ctg x, sec x, cosec x también lo son.
Función tangente f(x) = tg x
Para la función tangente, los valores de discontinuidad son: ± π/2, ± 3π/2, ± 5π/2… Allí la función toma valores muy grandes o muy pequeños. En general esto sucede para todos los múltiplos de π de la forma (2n+1) π/2, tanto positivos como negativos, con n= 0, 1, 2…
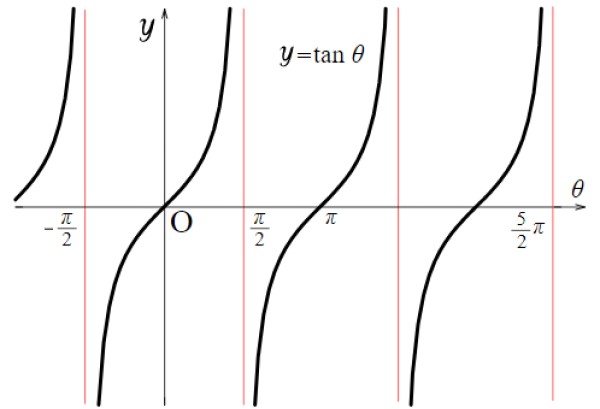
Por lo tanto:
Dominio de tg x: D = {x ∈ R / x ≠ (2n+1) π/2; n ∈ Z}
Rango o recorrido de tg x: Todos los reales.
Nótese que la función f(x) = tg x se repite entre – π/2 y + π/2, por lo tanto su período es π. Además, es simétrica respecto al origen.
Función cotangente f(x) = ctg x
Para esta función los valores de discontinuidad ocurren en 0, ± π, ± 2π…, es decir, los múltiplos enteros de π.
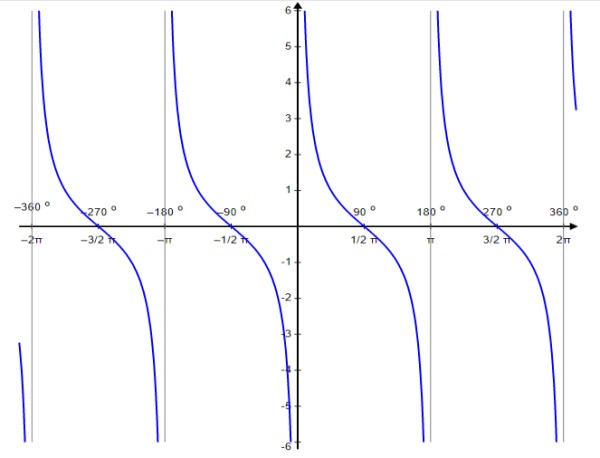
Al igual que la función tangente, la función cotangente es periódica de período π. Para ella se cumple que:
Dominio de ctg x: D = {x ∈ R / x ≠ n π; n ∈ Z}
Rango o recorrido de ctg x: Todos los reales.
Función secante f(x) = sec x
La función sec x tiene puntos de discontinuidad en ± π/2, ± 3π/2, ± 5π/2…, donde cos x = 0. Asimismo es periódica de período π y también se observa de la gráfica que la función jamás toma valores en el intervalo (-1,1)
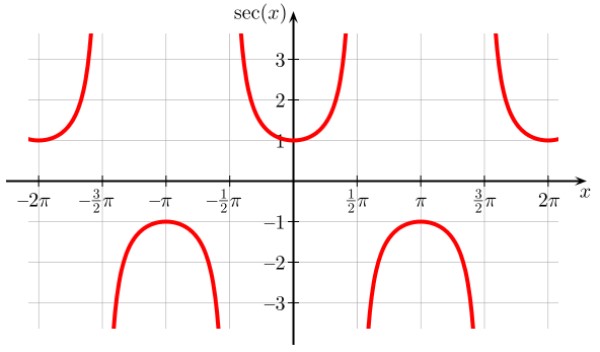
Dominio de sec x: D = {x ∈ R / x ≠ (2n+1) π/2; n ∈ Z}
Rango o recorrido de sec x: Todos los reales excepto (-1,1)
Función cosecante f(x) = cosec x
Es semejante a la función secante, aunque está desplazada hacia la derecha, por lo tanto los puntos de discontinuidad son 0, ±π, ± 2π y todos los múltiplos enteros de π. Asimismo es periódica.
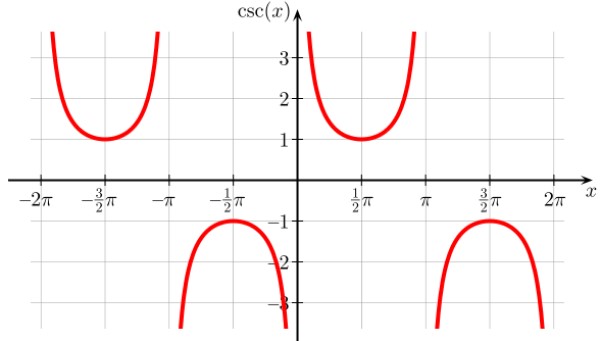
Dominio de cosec x: D = {x ∈ R / x ≠ n π; n ∈ Z}
Rango o recorrido de cosec x: Todos los reales excepto (-1,1)
Un hombre de 6 pies de estatura proyecta una sombra S cuyo largo viene dado por:
S (t) = 6 │cot (π.t/12) │
Con S en pies y t el número de horas transcurridas a partir de las 6 AM. ¿Cuánto mide la sombra a las 8 AM, a las 12 M, a las 2 PM y a las 5:45 PM?
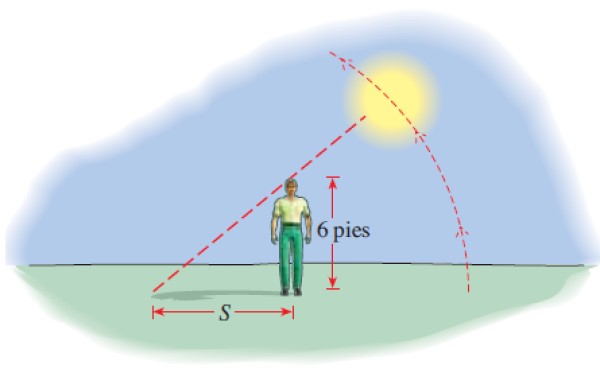
Debemos evaluar la función para cada uno de los valores dados, nótese que debe tomar el valor absoluto, ya que la longitud de la sombra es positiva:
-A las 8 AM han transcurrido 2 horas a partir de las 6 AM, por lo tanto t = 2 y S(t) es:
S (2) = 6 │cot (π.2/12) │pies = 6 │cot (π/6) │pies = 10.39 pies.
-Cuando son las 12 N, han transcurrido t = 6 horas, por lo tanto:
S (6) = 6 │cot (π.6/12) │pies = 6 │cot (π/2) │pies = 0 pies. (A esa hora el Sol cae verticalmente sobre la cabeza de la persona).
-A las 2 PM pasaron t = 8 horas:
S (8) = 6 │cot (π.8 /12) │pies = 6 │cot (2π/3) │pies = 3.46 pies.
-Cuando son las 5:45 PM ya pasaron 11.75 horas desde las 6 AM, entonces:
S (11.75) = 6 │cot (π x 11.75 /12) │pies = 91.54 pies. A esta hora las sombras son cada vez más largas.
¿Puede el lector calcular la hora en que la sombra de la persona es igual a su altura?
- Carena, M. 2019. Manual de Matemática Preuniversitaria. Universidad Nacional del Litoral.
- Figuera, J. 1999. Matemática. 1ro. Diversificado. Ediciones Colegial Bolivariana.
- Hoffman, J. Selección de temas de Matemática. Volumen 4.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Zill, D. 1984. Álgebra y Trigonometría. McGraw Hill.
