Valor relativo: qué es, ejemplos, ejercicios resueltos

¿Qué es el valor relativo de un número?

El valor relativo de un número o dígito del sistema decimal depende de la posición que ocupa cuando forma parte de una cifra. Por lo tanto, se dice que es un valor posicional. Un ejemplo muy sencillo: el valor relativo de 1 en el número 123, será de 100, pues el 1 ocupa la posición de las centenas.

Otro ejemplo: el número 58 está formado por los dígitos 5 y 8. Examinando esta cifra de derecha a izquierda se tiene que el valor relativo del 8 es 8, por estar en la posición de las unidades y el valor relativo del 5 es 50, por ocupar el sitio de las decenas. El número se lee “cincuenta y ocho”.

En cambio, los mismos dígitos tienen valores relativos diferentes en el número 85, ya que han intercambiado posiciones. Siempre comenzando de derecha a izquierda, el valor relativo del 5 en este caso es 5, el valor relativo del 8 es 80 y el número se lee “ochenta y cinco”.

¿Cómo hallar el valor relativo de un número?

El procedimiento general para hallar el valor relativo de cada dígito es como sigue:

• El primer dígito de derecha a izquierda se encuentra en la posición de las unidades y su valor se multiplica por 1.
• El siguiente dígito corresponde a las decenas y se multiplica por 10.
• La próxima posición corresponde a las centenas y el valor del dígito se multiplica por 100.
• La siguiente posición es el millar, por lo tanto el dígito se multiplica por 1000.

Y así sucesivamente para números más grandes, multiplicando el dígito por la potencia de 10 correspondiente: 100000, 1000000 y más allá.

Por ejemplo, el número 321 se puede escribir como 3*100 + 2*10 + 1*1, o equivalentemente 300+20+1. En el ejemplo anterior, se puede apreciar de forma rápida que el valor relativo de 3 es 300, de 2 es 20 y de 1 es 1.

Ejemplos de valores relativos

Número 727

Para determinar el valor relativo de un dígito hay que guiarse por el siguiente principio básico de la numeración escrita del sistema decimal:

Cualquier dígito a la izquierda de otro representa una unidad 10 veces mayor, y a la inversa: todo dígito a la derecha de otro, representa una unidad 10 veces menor. 

Por ejemplo la cifra 727, que se lee “setecientos veinte y siete”, consta de los dígitos 2 y 7, con el 7 repetido, pero ocupando posiciones diferentes.

Leyendo 727 de derecha a izquierda, se observa que el 7 de la derecha ocupa la posición de la unidad, por lo tanto se multiplica por 1:

7 x 1 = 7

Y su valor relativo es 7.

El dígito 2 en el medio ocupa la posición de las decenas y para hallar su valor relativo se le multiplica por 10:

2 x 10 = 20

Finalmente el 7 a la extrema izquierda tiene la posición de las centenas. Entonces hay que multiplicarlo por 100 y su valor relativo es:

7 x 100 = 700

Nótese que únicamente cuando el dígito ocupa la posición de la unidad es que su valor absoluto y su valor relativo son iguales. Por lo tanto, si el valor relativo del número es VR y su valor absoluto es VA, la fórmula general para hallar el valor relativo es:

VR = valor absoluto VA × valor de su posición

Una cifra se puede escribir como la suma de los valores relativos de sus dígitos, a esto se le conoce como notación desarrollada. Siguiendo con el ejemplo del número 727 se tiene que:

727 = 700 + 20 + 7

Y si se prefiere hacer uso de las potencias de 10, el número 727 también se expresa de manera equivalente como:

727 = 7∙10² + 2∙10¹ + 7∙10⁰

Donde los exponentes de la potencia en base 10 representan la posición de cada dígito y se llaman índices. En la siguiente figura se ilustra otro ejemplo.

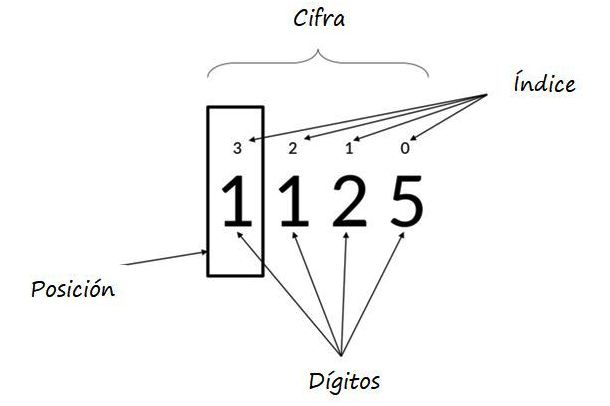
Número 63

Comenzando de izquierda a derecha, el 3 se encuentra en la posición de las unidades, por lo tanto:

Valor relativo del 3: 3 x 1 = 3

En cuanto al 6, este se encuentra en la posición de las decenas, luego:

Valor relativo del 6: 6 x 10 = 60

Número 603

Esta cifra es diferente de la anterior, porque aunque el valor relativo del 0 es 0, los demás dígitos tienen valores relativos diferentes. Comenzando de derecha a izquierda como siempre:

• Valor relativo del 3: 3 x 1 = 3
• Valor relativo del 0: 0 x 10 = 0
• Valor relativo del 6: 6 x 100 = 600

Número 630

En este caso el 0 se encuentra en la posición de las unidades:

• Valor relativo del 0: 0 x 1 = 0
• Valor relativo del 3: 3 x 10 = 30
• Valor relativo del 6: 6 x 100 = 600

Ejercicios resueltos

Ejercicio 1

Indicar el valor relativo de los números subrayados:

a) 1209

b) 2782

c) 376

d) 3045

e) 273

Solución

a) El dígito 1 en 1209 ocupa la posición del millar o lo miles. Por lo tanto, su valor relativo es 1000.

VR(1) = 1 x 1000 = 1000

b) El 2 ocupa la posición de las unidades en 2782, por lo tanto su valor relativo es 2.

c) En 376 el 7 está en la posición de las decenas y:

VR(7) = 7 x 10 = 70.

d) En  3045 el 4 también está en la posición de las decenas:

VR(4) = 4 x 10 = 40.

e) Para 273 el 3 se encuentra en el lugar de las unidades y su valor relativo coincide con la figura del dígito, es decir:

VR (3) = 3 x 1 = 3

Ejercicio 2

Escribir el menor número de 5 dígitos, sin que ninguno se repita y cumpliendo las siguientes condiciones:

a) Que todos los dígitos sean diferentes

b) Tiene un 7 en la posición del millar

c) El 8 esté en la posición de las unidades.

Solución a

El número más pequeño de 5 dígitos, con todos ellos diferentes, debe comenzar por 1, ya que aunque el 0 es menor, como primer dígito a la izquierda no cuenta, por lo tanto el número buscado es:

10234

Solución b

La posición del millar para el 7 corresponde a 7000, pero como se quiere la cifra más pequeña posible que contenga 5 dígitos, el número tiene que comenzar por 1, seguido del 7 y luego 023 en las restantes posiciones, ya que ningún dígito debe repetirse.

Por lo tanto el número es:

17023

Solución c

Como se pide que el 8 esté en la posición de las unidades, debe estar a la extrema derecha. Siendo el menor número posible, sin que ninguno de sus 5 dígitos se repita, el número buscado es:

10238

Ejercicio 3

Calcule el valor absoluto y relativo (de cada cifra) del número 579.

Solución

Se tiene que 579 es igual a 5×100+7×10+9×1, o de forma equivalente, es igual a 500+70+9. Por lo tanto el valor relativo de 5 es 500, el valor relativo de 7 es 70 y el de 9 es 9.

Por otro lado, el valor absoluto de 579 es igual a 579.

Ejercicio 4

Dado el número 9.648.736, ¿cuál es el valor relativo del 9 y del primer 6 (de izquierda a derecha)? ¿Cuál es el valor absoluto del número dado?

Solución

Al reescribir al número 9.648.736 se obtiene que este es equivalente a

9×1.000.000 + 6×100.000 + 4×10.000 + 8×1.000 + 7×100 + 3×10 + 6×1

o se puede escribir como

9.000.000 + 600.000 + 40.000 + 8.000 + 700 + 30 + 6.

De modo que el valor relativo de 9 es 9.000.000 y el valor relativo del primer 6 es 600.000.

Por otro lado, el valor absoluto del número dado es 9.648.736.