Absorbancia: qué es, ejemplos y ejercicios resueltos
La absorbancia es el logaritmo con signo negativo del cociente entre la intensidad luminosa emergente y la intensidad luminosa incidente sobre una muestra de solución traslúcida que ha sido iluminada con luz monocromática. Este cociente es la transmitancia.
El proceso físico del paso de la luz a través de una muestra se llama transmisión luminosa, y la absorbancia es una medida de ella. De aquí que la absorbancia viene a ser el menos logaritmo de la transmitancia y es un dato importante para determinar la concentración de una muestra que generalmente está disuelta en un solvente como agua, alcohol o cualquier otro.
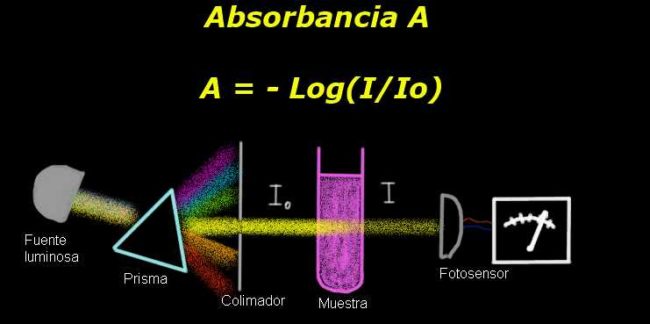
Para medir la absorbancia, se requiere de un dispositivo llamado electro-fotómetro, con el cual se mide una corriente que es proporcional a la intensidad luminosa incidente sobre su superficie.
Al momento de calcular la transmitancia, generalmente se mide primero la señal de la intensidad correspondiente al solvente solo y se registra este resultado como Io.
Luego se coloca la muestra disuelta en el solvente con la mismas condiciones de iluminación. La señal medida por el electro-fotómetro se denota como I, lo cual permite calcular la transmitancia T de acuerdo a la siguiente fórmula:
T = I / Io
Se trata de una cantidad sin dimensiones. La absorbancia A queda así expresada como:
A = – log (T) = – log(I / Io)
Índice del artículo
Las moléculas que componen una sustancia química son capaces de absorber la luz, y una medida de ello es precisamente la absorbancia. Es el resultado de la interacción entre los fotones y los electrones moleculares.
Por lo tanto se trata de una magnitud que dependerá de la densidad o concentración de las moléculas que componen la muestra y también del camino óptico o distancia recorrida por la luz.
Los datos experimentales señalan que la absorbancia A es linealmente proporcional a la concentración C y a la distancia d recorrida por la luz. De modo que para calcularla en función de estos parámetros, puede establecerse la siguiente fórmula:
A = ε⋅C⋅d
En la fórmula anterior, ε es una constante de proporcionalidad conocida con el nombre de absortividad molar.
La absortividad molar depende del tipo de sustancia y de la longitud de onda con la que se mide la absorbancia. La absortividad molar también es sensible a la temperatura de la muestra y al pH de la misma.
Esta relación entre la absorbancia, la absortividad, la concentración y la distancia del grosor del camino que sigue la luz dentro de la muestra se conoce con el nombre de ley de Beer-Lambert.

A continuación hay algunos ejemplos de cómo utilizarla.
Durante un experimento se ilumina una muestra con luz roja de un láser de helio-neón, cuya longitud de onda es 633 nm. Un electro-fotómetro mide 30 mV cuando la luz del láser incide directamente y 10 mV cuando pasa a través de una muestra.
En tal caso la transmitancia es:
T = I / Io = 10 mV / 30 mV = ⅓.
Y La absorbancia es:
A = – log(⅓) = log(3) = 0,48
Si la misma sustancia se coloca en recipiente que tiene la mitad del espesor del usado en el ejemplo 1, diga cuánto marcará el electro-fotómetro, cuando se hace pasar por la muestra la luz del láser de helio-neón.
Hay que considerar que si el espesor disminuye a la mitad, entonces la absorbancia que es proporcional al grosor óptico disminuye a la mitad, es decir A= 0,28. La transmitancia T estará dada por la siguiente relación:
T = 10-A = 10^(-0.28) = 0,53
El electro-fotómetro marcará 0,53*30 mV = 15,74 mV.
Se quiere determinar la absortividad molar de cierto compuesto patentado que se encuentra en disolución. Para ello se ilumina la solución con luz proveniente de una lámpara de sodio de 589 nm. La muestra será colocada en un portamuestra de 1,50 cm de espesor.
Se parte de una solución de concentración 4,00×10^-4 moles por litro y se mide la transmitancia dando como resultado 0,06. Determine con estos datos la absortividad molar de la muestra.
Solución
En primer lugar se determina la absorbancia, la cual se define como el menos logaritmo en base diez de la transmitancia:
A = – log (T)
A = – log (0,06) = 1,22
Luego se usa la ley de Lambert-Beer que establece una relación entre la absorbancia, la absortividad molar, la concentración y la longitud óptica:
A = ε⋅C⋅d
Despejando la absortividad molar se obtiene la siguiente relación:
ε = A/(C⋅d)
sustituyendo los valores dados se tiene:
ε = 1,22/(4,00×10^-4 M⋅1,5 cm)=2030 (M⋅cm)^-1
El resultado anterior se ha redondeado a tres dígitos significativos.
Con el fin de mejorar la precisión y determinar el error de la medida de la absortividad molar de la muestra en el ejercicio 1, se procede a diluir la muestra sucesivamente a la mitad de la concentración y se mide la transmitancia en cada caso.
Partiendo de Co = 4×10^-4 M con transmitancia T= 0,06 se obtiene la siguiente secuencia de datos para la transmitancia y de la absorbancia calculada a partir de la transmitancia:
Co/1–>0,06–>1,22
Co/2–>0,25–>0,60
Co/4–>0,50–>0,30
Co/8–>0,71–>0,15
Co/16–>0,83–>0,08
Co/32–>0,93–>0,03
Co/64–>0,95–>0,02
Co/128–>0,98–>0,01
Co/256–>0,99–>0,00
Con estos datos realice:
a) Una gráfica de la absorbancia en función de la concentración.
b) Un ajuste lineal de los datos y encuentre la pendiente.
c) De la pendiente obtenida, calcule la absortividad molar.
Solución
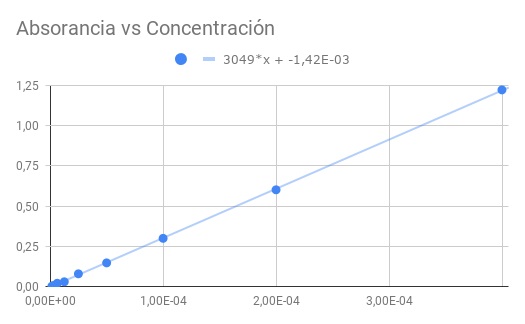
La pendiente obtenida es el producto de la absortividad molar por la distancia óptica, por lo que dividiendo la pendiente por la longitud 1,5 cm obtenemos la absortividad molar
ε = 3049/1,50 = 2033 (M⋅cm)^-1
Con los datos del ejercicio 2:
a) Calcule la absortividad para cada dato.
b) Determine un valor promedio para la absortividad molar, su desviación estándar y el error estadístico asociado al promedio.
Solución
Se calcula la absortividad molar para cada uno de las concentraciones ensayadas. Recordemos que las condiciones de iluminación y la distancia óptica se mantienen fijas.
Los resultados para la absortividad molar son:
2033, 2007, 2007, 1983, 2158, 1681, 2376, 1,872, 1862 en unidades de 1/(M*cm).
De estos resultados podemos tomar el valor promedio:
ε> = 1998 (M*cm)^-1
Con una desviación estándar de : 184 (M*cm)^-1
El error del promedio es la desviación estándar dividido entre la raíz cuadrada del número de datos, es decir:
Δε>= 184/9^0,5 = 60 (M*cm)^-1
Finalmente se concluye que la sustancia patentada tiene una absortividad molar a la frecuencia 589 nm producida por una lámpara de sodio de:
ε> = (2000 ± 60) (M*cm)^-1
- Atkins, P. 1999. Química Física. Ediciones Omega. 460-462.
- La guía. Transmitancia y absorbancia. Recuperado de: quimica.laguia2000.com
- Toxicología Ambiental. Transmitancia, absorbancia y ley de Lambert. Recuperado de: repositorio.innovacionumh.es
- Física aventura. Absorbancia y transmitancia. Recuperado de: rpfisica.blogspot.com
- Spectophotometry. Recobrado de: chem.libretexts.org
- Toxicología Ambiental. Transmitancia, absorbancia y ley de Lambert. Recuperado de: repositorio.innovacionumh.es
- Wikipedia. Absorbancia. Recuperado de: wikipedia.com
- Wikipedia. Espectrofotometría. Recuperado de: wikipedia.com
