Semicírculo: cómo calcular el perímetro, área, centroide, ejercicios
El semicírculo es una figura plana delimitada por un diámetro de la circunferencia y uno de los dos arcos circulares planos determinados por dicho diámetro.
De esta manera, un semicírculo está bordeado por una semicircunferencia, la cual consta de un arco circular plano y un segmento recto que une los extremos del arco circular plano. El semicírculo abarca la semicircunferencia y todos los puntos interiores a la misma.
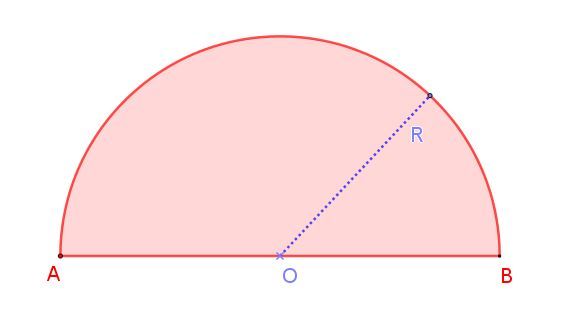
Esto lo podemos apreciar en la figura 1, que muestra un semicírculo de radio R, cuya medida es la mitad de la del diámetro AB. Nótese que a diferencia de un círculo, en el que hay infinitos diámetros, en la semicircunferencia sólo hay un diámetro.
El semicírculo es una figura geométrica con muchos usos en arquitectura y diseño, tal como vemos en la siguiente imagen:

Índice del artículo
Los elementos de un semicírculo son:
1.- El arco circular plano A⌒B
2.- El segmento [AB]
3.- Los puntos interiores a semicircunferencia compuesta por el arco A⌒B y el segmento [AB].
El perímetro es la suma del contorno del arco más la del segmento recto, por lo tanto:
Perímetro = longitud del arco A⌒B + longitud del segmento [AB]
En el caso de un semicírculo de radio R su perímetro P estará dado por la fórmula:
P = π⋅R + 2⋅R = (π + 2)⋅R
El primer término es la mitad del perímetro de una circunferencia de radio R, mientras que el segundo es la longitud del diámetro, el cual es el doble del radio.
Como un semicírculo es uno de los sectores angulares planos que quedan al trazar un diámetro por la circunferencia, su área A será la mitad del área del círculo que contiene al semicírculo de radio R:
A = (π⋅R2) / 2 = ½ π⋅R2
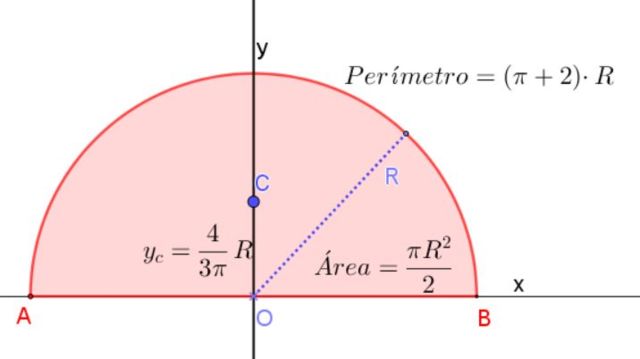
El centroide de un semicírculo está sobre su eje de simetría a una altura medida desde su diámetro de 4/(3π) veces el radio R.
Esto corresponde aproximadamente a 0,424⋅R, medido desde el centro del semicírculo y sobre su eje de simetría, tal como se muestra en la figura 3.
Se define el momento de inercia de una figura plana respecto a un eje, por ejemplo eje x, como:
La integral del cuadrado de la distancia de los puntos que pertenecen a la figura hasta el eje, siendo el diferencial de integración un elemento infinitesimal de área, tomado en la posición de cada punto.
En la figura 4 se muestra la definición del momento de inercia Ix del semicírculo de radio R, respecto del eje X que pasa por su diagonal:
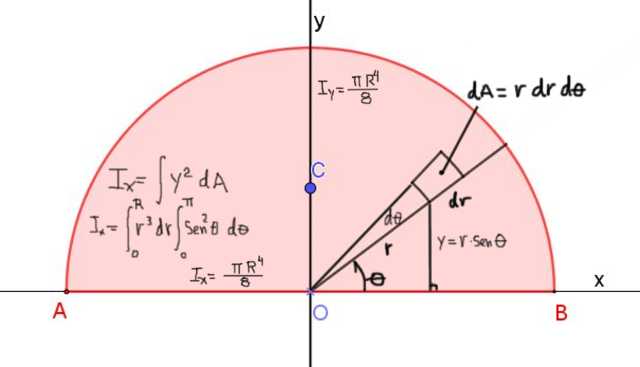
El momento de inercia respecto del eje x está dado por:
Ix = (π⋅R4) / 8
Y el momento de inercia respecto del eje de simetría y es:
Iy = (π⋅R4) / 8
Se nota que ambos momentos de inercia coinciden en su fórmula, pero es importante destacar que están referidos a ejes diferentes.
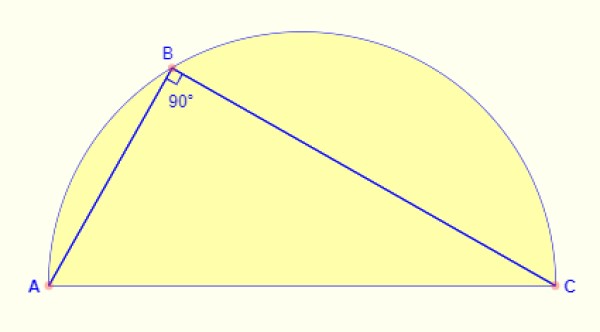
El ángulo inscrito en el semicírculo siempre es de 90º. Sin importar en que parte del arco se tome al punto, el ángulo que se forma entre los lados AB y BC de la figura siempre es recto.
Determine el perímetro de un semicírculo de radio 10 cm.
Solución
Recordemos que el perímetro en función del radio está dado por la fórmula que vimos anteriormente:
P = (2 + π)⋅R
P = (2 + 3,14)⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.
Hallar el área de un semicírculo de radio 10 cm.
Solución
La fórmula para el área de un semicírculo es:
A = ½ π⋅R2 = ½ π⋅(10cm)2 = 50π cm2 = 50 x 3,14 cm2 = 157 cm2.
Determinar la altura h del centroide de un semicírculo de radio R= 10 cm medida a partir de su base, siendo la misma el diámetro del semicírculo.
Solución
El centroide es el punto de equilibrio del semicírculo y su posición está sobre el eje de simetría a una altura h de la base (diámetro del semicírculo):
h = (4⋅R) / (3π) = (4⋅10 cm) / (3 x 3,14) = 4,246 cm
Hallar el momento de inercia de un semicírculo respecto de el eje que coincide con su diámetro, sabiendo que el semicírculo está hecho de una lámina delgada. Su radio es de 10 cm y su masa es de 100 gramos.
Solución
La fórmula que da el momento de inercia del semicírculo es:
Ix = (π⋅R4) / 8
Pero como el problema nos dice que se trata de un semicírculo material, entonces la relación anterior debe ser multiplicada por la densidad superficial de masa del semicírculo, la cual se denotará por σ.
Ix = σ(π⋅R4) / 8
Pasamos a continuación a determinar σ, que no es otra cosa que la masa del semicírculo dividido entre el área del mismo.
El área fue determinada en el ejercicio 2 y el resultado fue 157 cm2. Entonces la densidad superficial de este semicírculo será:
σ = 100 gramos / 157 cm2 = 0,637 g/cm2
Entonces el momento de inercia respecto del diámetro se calculará así:
Ix = (0,637 g/cm2) [3,1416 ⋅ (10cm)4] / 8
Dando como resultado:
Ix = 2502 g⋅cm2
Determinar el momento de inercia de un semicírculo de radio 10 cm construido de una lámina material con una densidad superficial de 0,637 g/cm2 por un eje que pase por su centroide y sea paralelo a su diámetro.
Solución
Para resolver este ejercicio es necesario recordar el teorema de Steiner sobre momentos de inercia de ejes paralelos, el cual dice así:
El momento de inercia I respecto de un eje que está a distancia h del centroide es igual a la suma del momento de inercia Ic respecto de un eje que pasa por el centroide y es paralelo al primero más el producto de la masa por el cuadrado de la separación de los dos ejes.
I = Ic + M h2
En nuestro caso se conoce I que es el momento de inercia respecto del diámetro, el cual ya fue calculado en el ejercicio 4. También se conoce la separación h entre el diámetro y el centroide, el cual fue calculado en el ejercicio 3.
Solo nos queda despejar Ic:
Ic = I – M h2
Ic = 2502 g⋅cm2 – 100g ⋅ (4,246 cm)2 dando como resultado que el momento de inercia por un eje paralelo al diámetro y que pasa por el centroide es:
Ic = 699,15 g⋅cm2
- Alexander, D. 2013. Geometría. 5ta. Edición. Cengage Learning.
- Math Open Reference. Semicircle. Recuperado de: mathopenref.com.
- Universo Fórmulas.Semicírculo. Recuperado de: universoformulas.com.
- Universo Fórmulas. Área de un Semicírculo. Recuperado de: universoformulas.com.
- Wikipedia. Semicircle. Recuperado de: en.wikipedia.com.
