Regla empírica: cómo aplicarla, para qué sirve, ejercicios resueltos
Una regla empírica es el resultado de la experiencia práctica y la observación de la vida real. Por ejemplo, se puede saber que especies de aves se pueden observar en ciertos lugares en cada época del año y de esa observación se puede establecer una “regla” que describa los ciclos de vida de estas aves.
En estadística, la regla empírica hace referencia a la forma de agrupación de las observaciones alrededor de un valor central, la media o promedio, en unidades de desviación estándar.

Supóngase que se tiene un grupo de personas con una altura promedio de 1.62 metros y una desviación estándar de 0.25 metros, entonces la regla empírica permitiría definir, por ejemplo, ¿Cuántas personas estarían en un intervalo de la media más o menos una desviación estándar?
Según la regla, el 68% de los datos se encuentra a más o menos una desviación estándar de la media, o sea, el 68% de las personas del grupo tendrá una altura entre 1.37 (1.62-0.25) y 1.87 (1.62+0.25) metros.
Índice del artículo
- 1 ¿De donde surge la regla empírica?
- 2 ¿Como aplicar la regla empírica?
- 3 ¿Para que sirve la regla empíríca?
- 4 Ejercicios resueltos
- 5 Referencias
La regla empírica es una generalización del Teorema de Tchebyshev y de la Distribución Normal.
El teorema de Tchebyshev dice que: para algún valor de k >1, la probabilidad de que una variable aleatoria se encuentre entre la media menos k veces la desviación estándar, y la media más k veces, la desviación estándar es mayor o igual que (1 – 1/k2).
La ventaja de este teorema es que se aplica a variables aleatorias discretas o continuas con cualquier distribución de probabilidad, pero la regla definida a partir de él no siempre es muy precisa, pues depende de la simetría de la distribución. Mientras más asimétrica sea la distribución de la variable aleatoria, menos ajustada a la regla será su comportamiento.
La regla empírica definida a partir de este teorema es:
Si k = √2, se dice que el 50% de los datos están en el intervalo: [µ – √2 s, µ + √2 s]
Si k = 2, se dice que el 75% de los datos están en el intervalo: [µ – 2 s, µ + 2 s]
Si k = 3, se dice que el 89% de los datos están en el intervalo: [µ – 3 s, µ + 3 s]
La distribución normal, o campana de Gauss, permite establecer la Regla Empírica o Regla 68 – 95 – 99.7.
La regla se basa en las probabilidades de ocurrencia de una variable aleatoria en intervalos entre la media menos una, dos o tres desviaciones estándar y la media más una, dos o tres desviaciones estándar.
La regla empírica define los siguientes intervalos:
El 68.27% de los datos están en el intervalo: [µ – s, µ + s]
El 95.45% de los datos están en el intervalo: [µ – 2s, µ + 2s]
El 99.73% de los datos están en el intervalo: [µ – 3s, µ + 3s]
En la figura se puede observar como se presentan estos intervalos y la relación entre ellos al aumentar el ancho de la base de la gráfica.
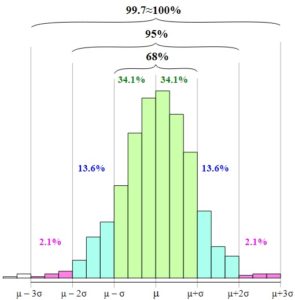
Por tanto, la aplicación de la regla empírica en escala de una variable normal estándar, z, define los siguientes intervalos:
El 68.27% de los datos están en el intervalo: [-1, 1]
El 95.45% de los datos están en el intervalo: [-2, 2]
El 99.73% de los datos están en el intervalo: [-3, 3]
La regla empírica permite abreviar cálculos cuando se trabaja con una distribución normal.
Supóngase que un grupo de 100 estudiantes universitarios tiene una edad promedio de 23 años, con una desviación estándar de 2 años. ¿Qué información permite obtener la regla empírica?
La aplicación de la regla empírica implica seguir los pasos:
1- Construir los intervalos de la regla
Dado que la media es 23 y la desviación estándar es 2, entonces los intervalos son:
[µ – s, µ + s] = [23 – 2, 23 + 2] = [21, 25]
[µ – 2s, µ + 2s] = [23 – 2(2), 23 + 2(2)] = [19, 27]
[µ – 3s, µ + 3s] = [23 – 3(2), 23 + 3(2)] = [17, 29]
2-Calcular la cantidad de estudiantes en cada intervalo de acuerdo a los porcentajes
(100)*68.27% = 68 estudiantes aproximadamente
(100)*95.45% = 95 estudiantes aproximadamente
(100)*99.73% = 100 estudiantes aproximadamente
3-Se asocian los intervalos de edades con las cantidades de estudiantes y se interpreta
Al menos 68 estudiantes tienen entre 21 y 25 años de edad.
Al menos 95 estudiantes tienen entre 19 y 27 años de edad.
Prácticamente los 100 estudiantes tienen entre 17 y 29 años de edad.
La regla empírica es una manera rápida y práctica de analizar datos estadísticos, siendo cada vez más confiable en la medida en que la distribución se acerca a la simetría.
Su utilidad depende del campo en que se use y de las preguntas que se presenten. Es muy útil saber que es casi improbable la ocurrencia de valores de tres desviaciones estándar por debajo o por encima de la media, incluso para las variables de distribución no normal, al menos el 88.8% de los casos está en el intervalo de tres sigma.
En las ciencias sociales, un resultado generalmente concluyente es el intervalo de la media más o menos dos sigma (95%), mientras que en física de partículas, un nuevo efecto requiere un intervalo cinco sigmas (99.99994%) para considerarse un descubrimiento.
En una reserva de fauna silvestre se estima que hay un promedio de 16.000 conejos con una desviación estándar de 500 conejos. Si se desconoce la distribución de la variable ‘número de conejos en la reserva’, ¿es posible estimar cuál es la probabilidad de que la población de conejos esté entre 15.000 y 17.000 conejos?
Se puede presentar el intervalo en estos términos:
15000 = 16000 – 1000 = 16000 – 2(500) = µ – 2 s
17000 = 16000 + 1000 = 16000 + 2(500) = µ + 2 s
Por tanto: [15000, 17000] = [µ – 2 s, µ + 2 s]
Aplicando el teorema de Tchebyshev, se tiene una probabilidad de al menos el 0.75 de que la población de conejos de la reserva de fauna silvestre esté entre 15.000 y 17.000 conejos.
El peso promedio de niños de un año en un país se distribuye normalmente con una media de 10 kilogramos y una desviación estándar de aproximadamente 1 kilogramo.
a) Estimar el porcentaje de niños de un año en el país que tienen un peso promedio entre 8 y 12 kilogramos.
8 = 10 – 2 = 10 – 2(1) = µ – 2 s
12 = 10 + 2 = 10 + 2(1) = µ + 2 s
Por tanto: [8, 12] = [µ – 2s, µ + 2s]
Según la regla empírica se puede afirmar que el 68.27% de los niños de un año del país tienen entre 8 y 12 kilogramos de peso.
b) ¿Cuál es la probabilidad de hallar un niño de un año de 7 kilogramos o menos de peso?
7 = 10 – 3 = 10 – 3(1) = µ – 3 s
Se sabe que 7 kilogramos de peso representa el valor µ – 3s, así como también se conoce que el 99.73% de los niños están entre 7 y 13 kilogramos de peso. Eso deja solo el 0.27% del total de niños para los extremos. La mitad de ellos, el 0.135%, tiene 7 kilogramos de peso o menos y la otra mitad, 0.135%, tiene 11 kilogramos de peso o más.
Entonces, se puede concluir que hay una probabilidad de 0.00135 de que un niño tenga 7 kilogramos de peso o menos.
c) Si la población del país alcanza 50 millones de habitantes y los niños de 1 año representan el 1% de la población del país, ¿Cuántos niños de un año tendrán un peso entre 9 y 11 kilogramos?
9 = 10 – 1 = µ – s
11 = 10 + 1 = µ + s
Por tanto: [9, 11] = [µ – s, µ + s]
De acuerdo con la regla empírica, el 68.27% de los niños de un año en el país están en el intervalo [µ – s, µ + s]
En el país hay 500000 niños de un año (el 1% de 50 millones), por lo que 341350 niños (el 68.27% de 500000) tienen entre 9 y 11 kilogramos de peso.
- Abraira, V. (2002). Desviación estándar y error estándar. Revista Semergen. Recuperado de web.archive.org.
- Freund, R.; Wilson, W.; Mohr, D. (2010). Statistical methods. Third ed. Academic Press-Elsevier Inc.
- servidor Alicante (2017). Regla empírica (Términos estadísticos). Recuperado de glosarios.servidor-alicante.com.
- Lind, D.; Marchal, W.; Wathen, S. (2012). Estadística aplicada a los negocios y la economía. Decimoquinta ed. McGraw-Hill/Interamericana de México S. A.
- Salinas, H. (2010). Estadística y probabilidades. Recuperado de uda.cl.
- Sokal, R.; Rohlf, F. (2009). Introduction to biostatistics. Second ed. Dover publications, Inc.
- Spiegel, M. (1976). Probabilidad y estadística. Serie Schaum. McGraw-Hill/Interamericana de México S. A.
- Spiegel, M.; Stephens, L. (2008). Estadística. Cuarta ed. McGraw-Hill/Interamericana de México S. A.
- Stat119 Review (2019). Solving empirical rule questions. Recuperado de stat119review.com.
- (2019). 68-95-99.7 rule. Recuperado de en.wikipedia.org.
