Dinámica de un sistema de partículas: ejemplos, ejercicios
La dinámica de un sistema de partículas consiste en la aplicación de las leyes de Newton del movimiento a un conjunto de partículas, el cual puede ser discreto (las partículas se pueden contar) o bien formar parte de un objeto extendido, en este caso el sistema es continuo.
Para explicar el movimiento de un sistema de partículas, resulta inconveniente analizar a cada una por separado y ver qué fuerzas actúan sobre ella. En vez de eso, se define un punto representativo del conjunto, llamado el centro de masas.
Describir el movimiento del centro de masas ofrece un panorama muy acertado del movimiento global del conjunto, además permite aplicar las leyes de Newton de forma análoga a cuando se considera al objeto como una partícula sin dimensiones.
Este último modelo, llamado modelo de partícula, es bueno para describir traslaciones y también cuando no es necesario considerar las dimensiones del objeto. Pero los objetos ordinarios tienen tamaño y si también tienen movimiento de rotación, es preciso tomar en cuenta los puntos sobre los cuales se aplican las fuerzas.
Índice del artículo

Un conjunto de partículas discretas m1, m2, m3… que eventualmente se mueve respecto al origen de un sistema de coordenadas, debido a alguna fuerza resultante que actúa sobre ellas es un buen ejemplo de sistema de partículas.
La Tierra se puede considerar como una partícula y la Luna otra, entonces ambas constituyen un sistema de 2 partículas bajo la acción de la fuerza de gravedad del Sol.
Una persona, un animal o cualquier objeto del entorno, también se puede considerar como un sistema de partículas, solo que estas son tan pequeñas, que no se pueden contar una a una. Este es un sistema continuo, pero tomando en cuenta ciertas consideraciones, su tratamiento es el mismo que para un sistema discreto.
A continuación están los detalles.
Para empezar el estudio de un sistema de partículas hay que hallar el centro de masas (CM), que es el punto donde se concentra toda la masa del sistema.
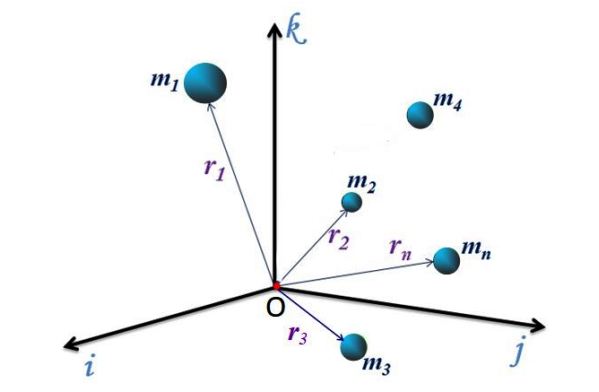
Para el sistema discreto de la figura 1, con n partículas, cada una tiene un vector de posición dirigido desde el origen O del sistema de coordenadas hasta el punto P(x,y,z) donde está la partícula. A estos vectores se los denota como r1, r2, r3… rn.
Las coordenadas del CM se calculan mediante las siguientes ecuaciones:
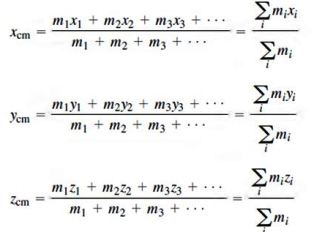
Donde cada de las masas del conjunto se representa como m1, m2, m3 …mn. Obsérvese que la sumatoria ∑ mi equivale a la masa total M del conjunto. Si el sistema es continuo, las sumatorias se sustituyen con integrales.
Cada una de las direcciones perpendiculares está representada por los vectores unitarios i, j y k, por lo tanto, el vector de posición del CM, denotado rCM, se puede expresar mediante:
rCM = xCM i + yCMj + zCMk
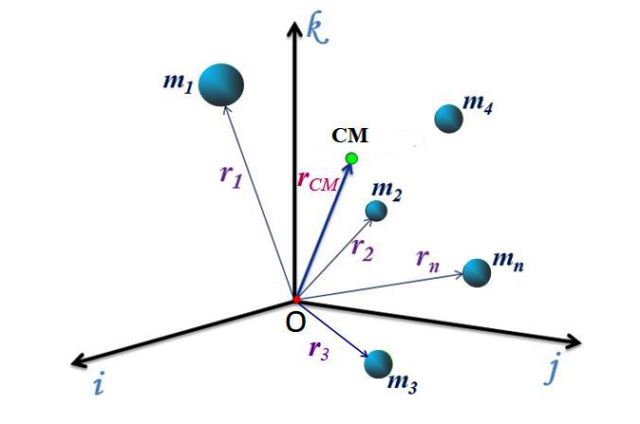
Una vez que se conoce la ubicación del centro de masas, se aplican las ecuaciones conocidas del movimiento. La velocidad del CM es la primera derivada de la posición respecto al tiempo:
En este caso, el sistema tiene una cantidad de movimiento total P que se calcula como el producto de la masa total del sistema y la velocidad del centro de masas:
P = M∙vCM
Alternativamente, la cantidad de movimiento total del sistema se puede calcular directamente:
P = m1v1 + m2v2 + m3v3 +…. = ∑ mi vi
Mientras que la aceleración del CM es la derivada de la velocidad:
Las fuerzas que actúan sobre un sistema de partículas pueden ser:
- Fuerzas internas, debido a interacciones entre las mismas partículas.
- Fuerzas externas, causadas por agentes externos al sistema.
Como las fuerzas internas se presentan por pares, de igual magnitud y dirección, pero sentidos opuestos, según la tercera ley de Newton, se cumple que:
∑ Fint = 0
Por lo tanto, las fuerzas internas no alteran el movimiento del conjunto, pero sí son muy importantes para determinar la energía interna.
Si el sistema está aislado y no hay fuerzas externas, según la primera ley de Newton el centro de masas está en reposo o se mueve con movimiento rectilíneo uniforme. En caso contrario, el centro de masa experimenta una aceleración dada por:
∑ Fext = M∙aCM
Donde M es la masa total del sistema. La ecuación anterior se puede escribir así:
Y significa que la fuerza externa equivale a la variación temporal en la cantidad de movimiento, otra forma de expresar la segunda ley de Newton y la misma que usó el famoso físico inglés en su libro Principia.
El centro de masas de un sistema de 2 partículas se encuentra sobre el eje x en un determinado momento, en la posición x = 2.0 m y moviéndose con velocidad 5.0 m/s en esa misma dirección y con sentido positivo. Si una de las partículas está en el origen y la otra, de masa 0.1 kg, está en reposo en x = 8.0 m, calcular:
a) La masa de la partícula que está en el origen.
b) Cantidad de movimiento del sistema
c) ¿Qué velocidad tiene la partícula que está en el origen?
De la ecuación para la posición del centro de masas:
rCM = xCM i + yCMj + zCMk = 2.0 m i
Como el CM tiene coordenada en x únicamente, se usa nada más la primera ecuación del trío dado previamente:
Ahora se sustituyen las coordenadas, si se denota a la partícula en el origen como la número 1 y a la otra como la número 2, los datos numéricos son:
x1 = 0 m, x2 = 8.0 m, m2 = 0.1 kg, xCM = 2.0 m
Quedando:
La cantidad de movimiento del sistema se calcula mediante:
P = M∙vCM
La masa total M es igual a:
M = 0.3 kg + 0.1 kg = 0.4 kg
Por lo tanto:
P = 0.4 kg∙5.0 m/s i = 2 kg.m/s i
De la ecuación para P de un sistema de dos partículas, se despeja v1, ya que los demás datos se conocen, pues el enunciado dice que la partícula 2 está en reposo, por lo tanto:
v2 = 0
Y P queda simplemente como:
P = m1v1
v1 = P / m1 = 2 kg.m/s i / 0.3kg = 6.67 m/s i
- Duke University. Systems of Particles. Recuperado de: webhome.phy.duke.edu.
- Rex, A. 2011. Fundamentos de Física. Pearson.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1. Pearson.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.
- Tipler, P. (2006) Física para la Ciencia y la Tecnología. 5ta Ed. Volumen 1. Editorial Reverté.
