Paralelepípedo: qué es, elementos, características, tipos, área, volumen

¿Qué es un paralelepípedo?

Un paralelepípedo es un cuerpo geométrico formado por seis caras, cuya característica principal es que todas sus caras son paralelogramos y además sus caras opuestas son paralelas entre sí. Se trata de un poliedro común en nuestra vida cotidiana, ya que lo podemos encontrar en las cajas de zapatos, la forma de un ladrillo, la forma de un microondas, etc.

Siendo un poliedro, el paralelepípedo encierra un volumen finito y todas sus caras son planas. Forma parte del grupo de los prismas, que son aquellos poliedros en los que todos sus vértices están contenidos en dos planos paralelos.

Elementos del paralelepípedo

Caras

Son cada una de las regiones formadas por paralelogramos que limitan al paralelepípedo. Un paralelepípedo posee seis caras, donde cada cara tiene cuatro caras adyacentes y una opuesta. Además, cada cara es paralela con su opuesta.

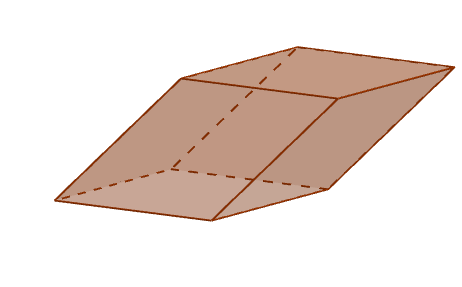
Aristas

Son el lado común de dos caras. En total, un paralelepípedo posee doce aristas.

Vértice

Es el punto en común de tres caras que son adyacentes entre sí dos a dos. Un paralelepípedo tiene ocho vértices.

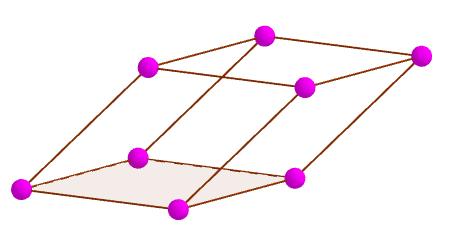
Diagonal

Dadas dos caras de un paralelepípedo opuestas entre sí, podemos trazar un segmento de recta que va desde el vértice de una cara hacia el vértice opuesto de la otra.

Este segmento se conoce como diagonal del paralelepípedo. Cada paralelepípedo posee cuatro diagonales.

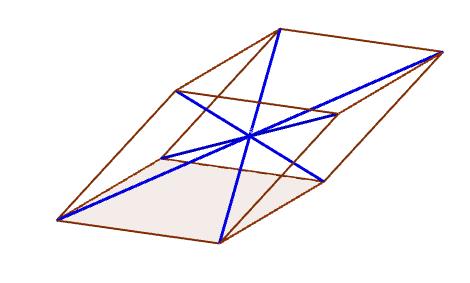
Centro

Es el punto en el cual se intersectan todas las diagonales.

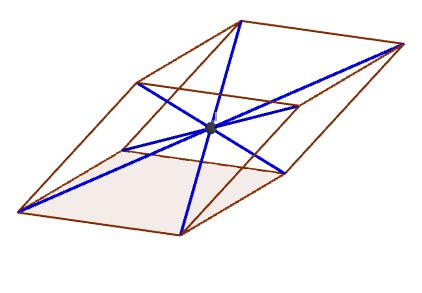
Características del paralelepípedo

Como ya mencionamos, este cuerpo geométrico posee doce aristas, seis caras y ocho vértices.

En un paralelepípedo pueden identificarse tres conjuntos formados por cuatro aristas, las cuales son paralelas entre sí. Además, las aristas de dichos conjuntos también cumplen con la propiedad de poseer la misma longitud.

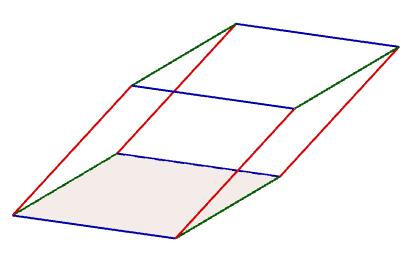
Otra propiedad que poseen los paralelepípedos es que son convexos, es decir si tomamos un par de puntos cualesquiera pertenecientes al interior del paralelepípedo, el segmento determinado por dicho par de puntos también estará en el interior del paralelepípedo.

Además, los paralelepípedos, al ser poliedros convexos, cumplen con el teorema de Euler para poliedros, el cual nos da una relación entre el número de caras, el número de aristas y el número de vértices. Esta relación está dada en forma de la siguiente ecuación:

C + V = A + 2

Esta característica se conoce como característica de Euler. Donde C es el número de caras, V el número de vértices y A el número de aristas.

Tipos de paralelepípedos

Podemos clasificar los paralelepípedos basándonos en sus caras, en los siguientes tipos:

Ortoedro

Son los paralelepípedos donde sus caras están formadas por seis rectángulos. Cada rectángulo es perpendicular con aquellos con que comparte arista. Son los más comunes en nuestra vida cotidiana, siendo esta la forma habitual de las cajas de zapatos y ladrillos.

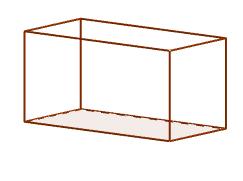
Cubo o hexaedro regular

Este es un caso particular del anterior, en donde cada una de las caras es un cuadrado.

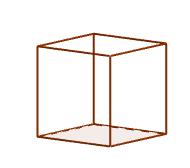
El cubo también es parte de los cuerpos geométricos denominados sólidos platónicos. Un sólido platónico es un poliedro convexo, de forma que tanto sus caras como sus ángulos internos son iguales entre sí.

Romboedro

Es un paralelepípedo que tiene por cara rombos. Estos rombos son todos iguales entre sí, ya que comparten aristas.

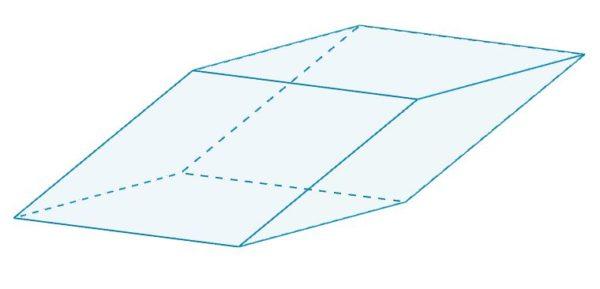
Romboiedro

Sus seis caras son romboides. Recordemos que un romboide es un polígono de cuatro lados y cuatro ángulos que son iguales dos a dos. Los romboides son los paralelogramos que no son ni cuadrados, ni rectángulos, ni rombos.

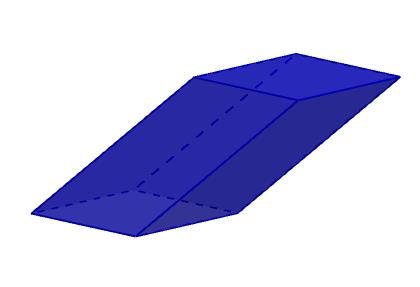
Por otra parte, los paralelepípedos oblicuos son aquellos en los que al menos una altura no concuerda con su arista. En esta clasificación podemos incluir a los romboedros y romboiedros.

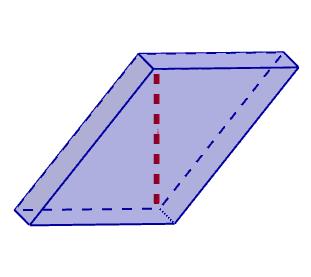
Cálculo de diagonales

Para calcular la diagonal de un ortoedro podemos usar el teorema de Pitágoras para R³.

Recordemos que un ortoedro tiene la característica de que cada lado es perpendicular con los lados que comparte arista. De este hecho podemos deducir que cada arista es perpendicular con aquellas que comparte vértice.

Para calcular la longitud de una diagonal de un ortoedro procedemos de la siguiente manera:

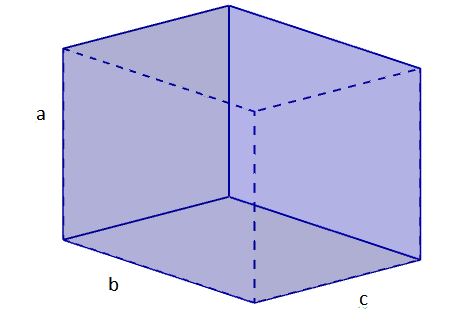
1. Calculamos la diagonal de una de las caras, la cual pondremos por base. Para esto usamos el teorema de Pitágoras. Nombremos a dicha diagonal d_b.

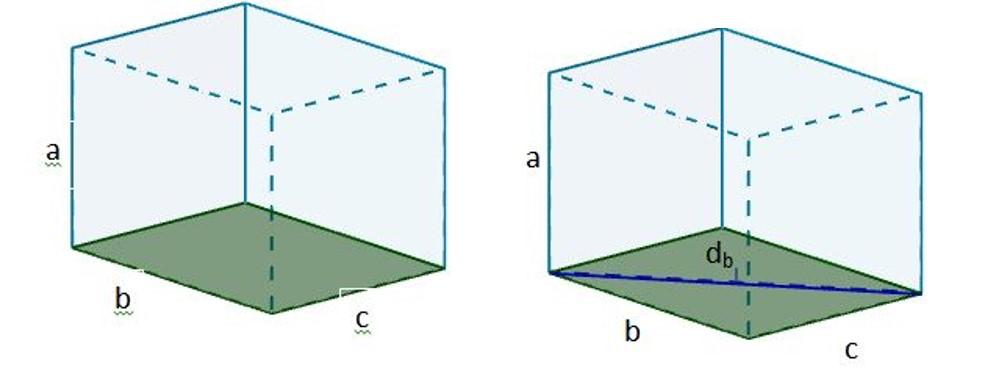
2. Luego con d_b podemos formar un nuevo triángulo rectángulo, tal que la hipotenusa de dicho triángulo sea la diagonal D buscada.

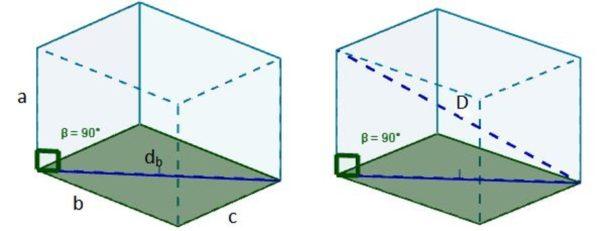
3. Usamos de nuevo el teorema de Pitágoras y tenemos que la longitud de dicha diagonal es:

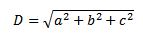
Otra forma de calcular diagonales de una manera más gráfica es con la suma de vectores libres.

Recordemos que dos vectores libres A y B se suman colocando la cola del vector B con la punta del vector A.

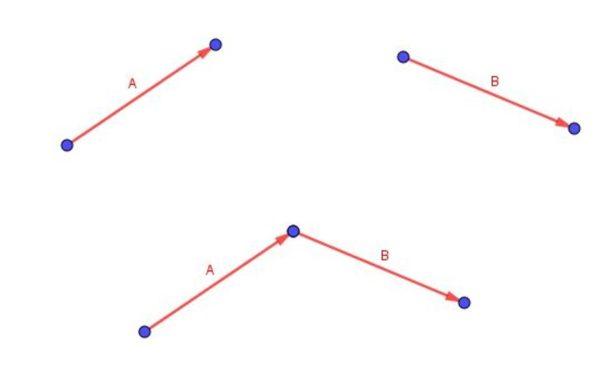
El vector (A + B) es aquel que comienza en la cola de A y termina en la punta de B.

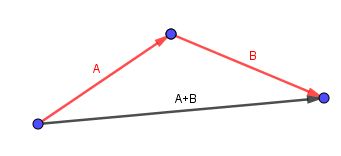
Consideremos un paralelepípedo al que deseamos calcular una diagonal. Identificamos las aristas con vectores orientados de manera conveniente.

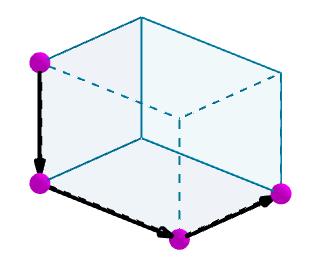
Luego sumamos dichos vectores y el vector resultante va a ser la diagonal del paralelepípedo.

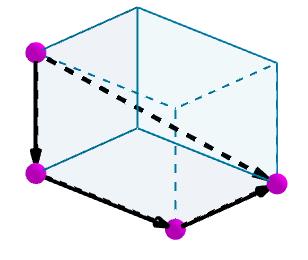
Área de un paralelepípedo

El área de un paralelepípedo viene dada por la suma de cada una de las áreas de sus caras.

Si determinamos uno de los lados como la base,

A_L + 2A_B = Área Total

Donde A_L es igual a la suma de las áreas de todos los lados adyacentes a la base, llamada área lateral y A_B es el área de la base.

Dependiendo del tipo de paralelepípedo con el que estemos trabajando podemos reescribir dicha fórmula.

Área de un ortoedro

Viene dada por la fórmula

A = 2 (ab + bc + ca).

Ejemplo 1

Dado el siguiente ortoedro, con lados a = 6 cm, b = 8 cm y c = 10 cm, calcular el área del paralelepípedo y la longitud de su diagonal.

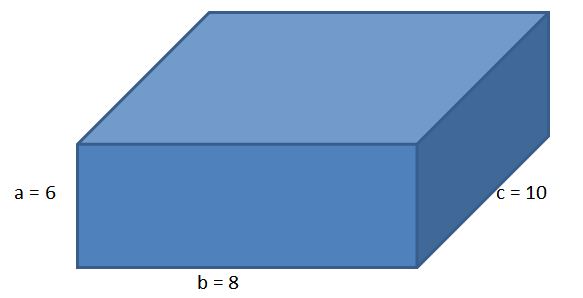
Usando la fórmula para el área de un ortoedro tenemos que

A = 2[(6)(8) + (8)(10) + (10)(6)] = 2[48 + 80 + 60] = 2[188] = 376 cm².

Nótese que como es un ortoedro la longitud de cualquiera de sus cuatro diagonales es la misma.

Usando el teorema de Pitágoras para el espacio tenemos que

D = (6² + 8² + 10²)^1/2 = (36 + 64 + 100)^1/2 = (200)^1/2

Área de un cubo

Como cada arista tiene la misma longitud, tenemos que a = b y a = c. Sustituyendo en la fórmula anterior tenemos

A = 2(aa + aa + aa) = 2(3a²) = 6a²

A = 6a²

Ejemplo 2

La caja de una consola de juegos posee la forma de un cubo. Si deseamos envolver dicha caja con papel para regalos, ¿cuánto papel gastaríamos sabiendo que la longitud de las aristas del cubo son 45 cm?

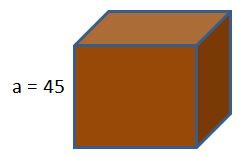
Usando la fórmula del área del cubo obtenemos que

A = 6(45 cm)² = 6(2025 cm²) = 12150 cm²

Área de un romboedro

Como todas sus caras son iguales, basta con calcular el área de una de ellas y multiplicarla por seis.

Tenemos que el área de un rombo la podemos calcular mediante sus diagonales con la siguiente fórmula

A_R = (Dd)/2

Usando esta fórmula se deduce que el área total del romboedro es

A_T = 6(Dd)/2 = 3Dd.

Ejemplo 3

Las caras del siguiente romboedro están formadas por un rombo cuyas diagonales son D = 7 cm y d = 4 cm. Su área será

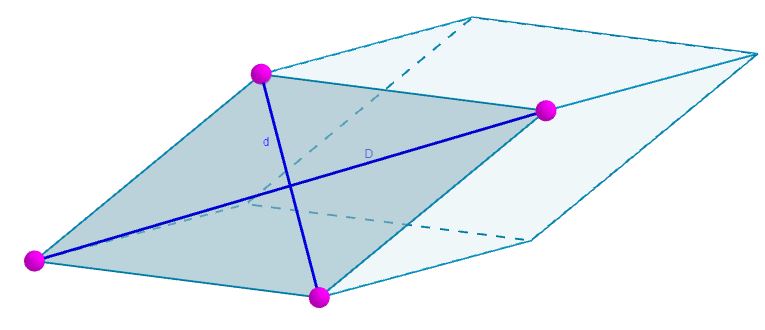
A = 3(7 cm)(4 cm) = 84 cm².

Área de un romboiedro

Para calcular el área de un romboiedro debemos calcular el área de los romboides que lo componen. Como los paralelepípedos cumplen con la propiedad de que los lados opuestos poseen la misma área, podemos asociar los lados en tres pares.

De esta manera tenemos que su área será

A_T = 2b₁h₁ + 2b₂h₂ + 2b₃h₃

Donde los b_i son las bases asociadas a los lados y los h_i su altura relativa correspondiente a dichas bases.

Ejemplo 4

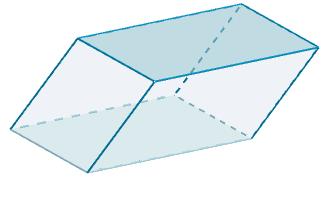
Considere el siguiente paralelepípedo,

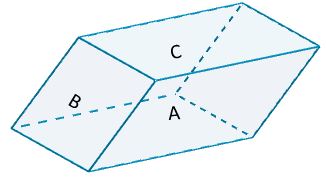
donde el lado A y el lado A’ (su lado opuesto) tienen por base b = 10 y por altura h = 6. El área marcada tendrá un valor de

A₁ = 2(10)(6) =120

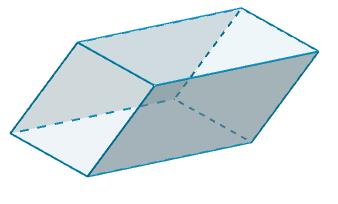
El B y B’ tienen b = 4  y h = 6, entonces

A₂ = 2(4)(6) = 48

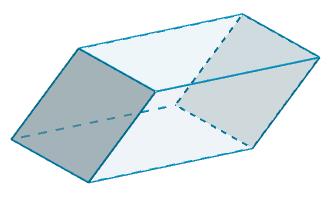
Y C y C’ tienen b = 10 y h = 5, así

A₃ = 2(10)(5) =100

Finalmente el área del romboiedro es

A = 120 + 48 + 100 = 268.

Volumen de un paralelepípedo

La fórmula que nos da el volumen de un paralelepípedo es el producto del área de una de sus caras por la altura correspondiente a dicha cara.

V = A_Ch_C

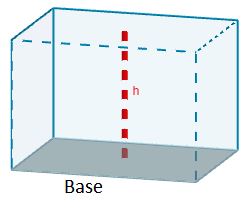
Dependiendo del tipo de paralelepípedo, dicha fórmula puede ser simplificada.

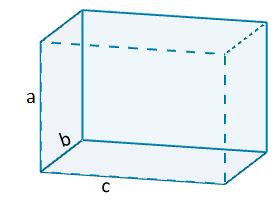
Así tenemos, por ejemplo, que el volumen de un ortoedro vendría dado por

V = abc.

Donde a, b y c representan la longitud de las aristas del ortoedro.

Y en el caso particular del cubo es

V = a³

Ejemplo 1

Se tienen tres modelos diferentes para cajas de galletas y se desea saber en cuál de dichos modelos se pueden guardar más galletas, es decir, cuál de las cajas tiene mayor volumen.

El primero es un cubo cuya arista posee una longitud de a = 10 cm.

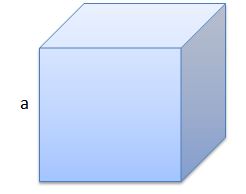
Su volumen será V = 1000 cm³

El segundo tiene por aristas b = 17 cm, c = 5 cm, d = 9 cm.

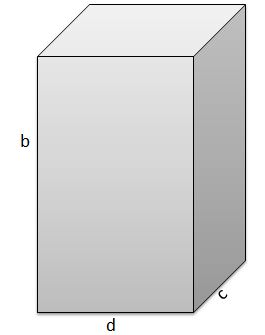
Y por lo tanto su volumen es de V = 765 cm³

Y la tercera tiene e = 9 cm, f = 9 cm y g = 13 cm.

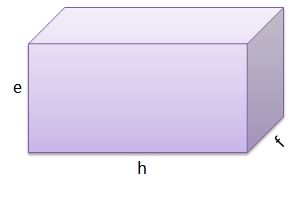
Y su volumen es de V = 1053 cm³

Por lo tanto, la caja con mayor volumen es la tercera.

Otro método para obtener el volumen de un paralelepípedo es recurrir al álgebra vectorial. En particular, el triple producto escalar.

Una de las interpretaciones geométricas que tiene el triple producto escalar es la del volumen del paralelepípedo, cuyas aristas son tres vectores que comparten un mismo vértice como punto de partida.

De esta manera, si tenemos un paralelepípedo y deseamos saber cuál es su volumen, basta con representarlo en un sistema de coordenadas en R³ haciendo coincidir uno de sus vértices con el origen.

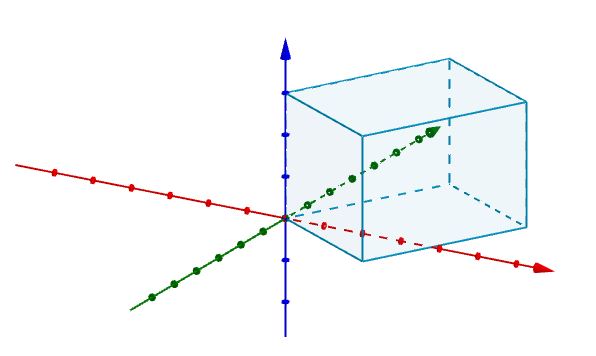
Luego representamos las aristas que concurren en el origen con vectores, como se muestra en la figura.

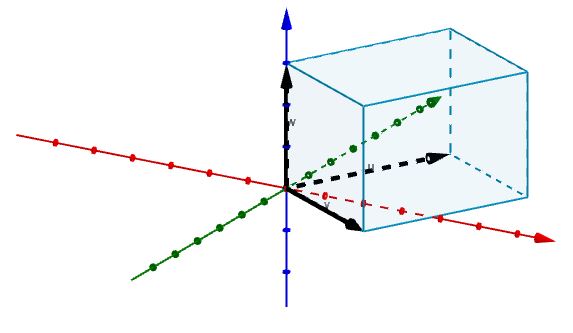
Y de esta manera tenemos que el volumen de dicho paralelepípedo viene dado por

V =| AxB ∙ C|

O de manera equivalente, el volumen es el determinante de la matriz 3×3, formada por los componentes de los vectores arista.

Ejemplo 2

Al representar el siguiente paralelepípedo en R³ podemos observar que los vectores que lo determinan son los siguientes

u = (-1,-3,0) , v = (5, 0, 0) y w = (-0.25, -4, 4)

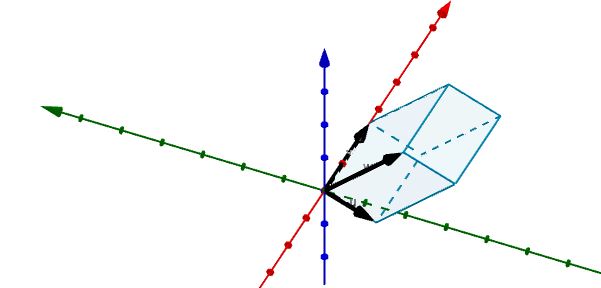
Usando el triple producto escalar tenemos

V = | (uxv)∙w|

uxv = (-1,-3,0) x  (5, 0, 0) = (0,0 ,– 15 )

(uxv)∙w = (0,0 ,– 15 ) ∙ (-0.25, -4, 4) = 0 + 0 + 4 (– 15) = – 60

De esto concluimos que V = 60

Consideremos ahora el siguiente paralelepípedo en R³ cuyas aristas vienen determinadas por los vectores

A = (2, 5, 0) , B = (6, 1, 0) y C = (3, 4, 4)

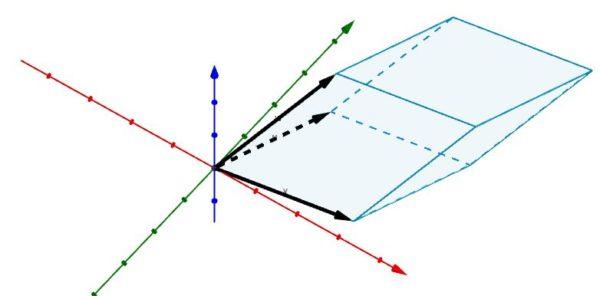
Usando determinantes nos da que

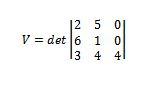
Así tenemos que el volumen de dicho paralelepípedo es de 112.

Ambas son maneras equivalentes de calcular el volumen.

Paralelepípedo perfecto

Se le conoce como ladrillo de Euler (o bloque de Euler) a un ortoedro que cumpla la propiedad de que tanto la longitud de sus aristas como la longitud de las diagonales de cada una de sus caras son números enteros.

Si bien Euler no fue el primer científico en estudiar los ortoedros que cumplen esa propiedad, sí encontró resultados interesantes sobre ellos.

El ladrillo de Euler más pequeño fue descubierto por Paul Halcke (1662-1731) y las longitudes de sus aristas son a = 44, b = 117 y c = 240.

Un problema abierto en la teoría de números es el siguiente:

¿Existen ortoedros perfectos?

En la actualidad, esta pregunta aún no tiene respuesta, ya que no se ha podido demostrar que no existan dichos cuerpos, pero tampoco se ha encontrado alguno.

Lo que se ha podido demostrar hasta ahora es que los paralelepípedos perfectos sí existen. El primero en ser descubierto tiene como longitud de sus aristas los valores 103, 106 y 271.

Referencias

1. Guy, R. (1981). Unsolved problems in number theory. Springer.
2. Landaverde, F. d. (1997). Geometría. Progreso.
3. Leithold, L. (1992). EL CÁLCULO con Geometría Analítica. HARLA, S.A.
4. Rendon, A. (2004). Dibujo técnico: Cuaderno de actividades 3 2do Bachillerato. Tebar.
5. Resnick, R., Halliday, D., & Krane, K. (2001). Física Vol. 1. México: Continental.