Transformaciones isométricas: concepto, composicion, tipos, ejemplos

Las transformaciones isométricas son cambios de posición u orientación de una determinada figura que no alteran ni la forma ni el tamaño de esta. Estas transformaciones son clasificadas en tres tipos: traslación, rotación y reflexión (isometría). En general, las transformaciones geométricas permiten crear una nueva figura a partir de otra dada.

Una transformación en una figura geométrica significa que, de alguna forma, esta fue sometida a algún cambio; es decir, que fue alterada. Según el sentido del original y el semejante en el plano, las transformaciones geométricas pueden clasificarse en tres tipos: isométricas, isomórficas y anamórficas.

Características de las transformaciones isométricas

– Las transformaciones isométricas se producen cuando se conservan las magnitudes de los segmentos y los ángulos entre la figura original y la transformada.

– En este tipo de transformación no se altera ni la forma ni el tamaño de la figura (son congruentes), solo se trata de un cambio de posición de esta, bien sea en la orientación o en el sentido. De esa forma, la figura inicial y la final serán semejantes y geométricamente congruentes.

– La isometría hace referencia a la igualdad; es decir, que las figuras geométricas serán isométricas si poseen la misma forma y tamaño.

– En las transformaciones isométricas lo único que se puede observar es un cambio de posición en el plano, ocurre un movimiento rígido gracias al cual la figura pasa de una posición inicial a una final. Esta figura es llamada homóloga (semejante) de la original.

– Existen tres tipos de movimientos que clasifican una transformación isométrica: traslación, rotación y reflexión o simetría.

Tipos de transformaciones isométricas

Por traslación

Son aquellas isometrías que permiten desplazar en línea recta todos los puntos del plano en una dirección y distancia determinada.

Cuando una figura se transforma por traslación esta no cambia su orientación con relación a la posición inicial, ni tampoco pierde sus medidas internas, las medidas de sus ángulos y lados. Este tipo de desplazamiento es definido por tres parámetros:

• Una dirección, que puede ser horizontal, vertical u oblicua.
• Un sentido, que puede ser hacia la izquierda, la derecha, arriba o abajo.
• Distancia o magnitud, que es la longitud que hay desde la posición inicial hasta la final de cualquier punto que se desplaza.

Para que una transformación isométrica por traslación se cumpla debe cumplir las siguientes condiciones:

• La figura siempre debe conservar todas sus dimensiones, tanto lineales como angulares.
• La figura no cambia su posición con respecto al eje horizontal; es decir, su ángulo nunca varía.
• Las traslaciones siempre serán resumidas en una sola, independientemente del número de traslaciones que se hagan.

En un plano donde el centro es un punto O, con coordenadas (0,0), la traslación queda definida por un vector T(a, b), que indica el desplazamiento del punto inicial. Es decir:

P(x, y) + T(a, b) = P’(x + a, y + b)

Por ejemplo, si al punto de coordenadas P (8, -2) se le aplica una traslación T (-4, 7), se obtiene:

P(8, -2) + T(-4, 7) = P’ [(8 + (-4)), ((-2) + 7)] = P’(4, 5)

En la siguiente imagen (izquierda) puede observarse cómo el punto C se trasladó hasta coincidir con el D. Lo hizo en dirección vertical, el sentido fue hacia arriba y la distancia o magnitud CD fue de 8 metros. En la imagen derecha se observa la traslación de un triángulo:

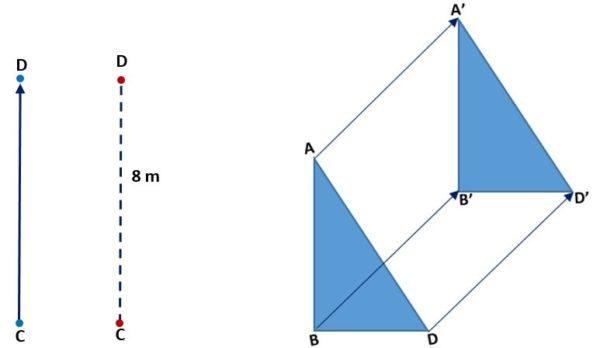
Por rotación

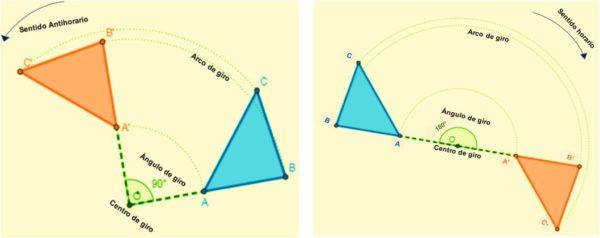
Son aquellas isometrías que permiten a la figura girar todos los puntos de un plano. Cada punto gira siguiendo un arco que tiene un ángulo constante y un punto fijo (centro de giro) determinados.

Es decir, toda rotación va a estar definida por su centro de rotación y ángulo de giro. Cuando una figura se transforma por rotación, mantiene la medida de sus ángulos y lados.

La rotación ocurre en un sentido determinado, es positiva cuando el giro es antihorario (sentido contrario a como giran las manecillas del reloj) y negativa cuando su giro es en sentido horario.

Si un punto (x, y) es rotado con respecto al origen —es decir, su centro de rotación es (0,0)—, en un ángulo de 90^o a 360^o las coordenadas de los puntos serán:

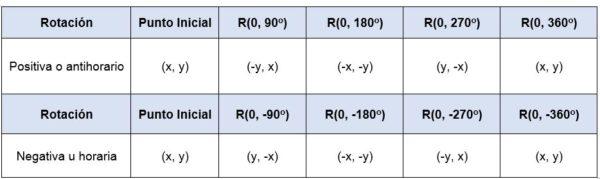
En el caso en el que la rotación no tiene centro en el origen, se debe trasladar el origen del sistema de coordenadas al nuevo origen dado, para así poder rotar la figura teniendo como centro el origen.

Por ejemplo, si al punto P(-5,2) se le aplica una rotación de 90^o, en torno al origen y en sentido positivo sus coordenadas nuevas serán (-2,5).

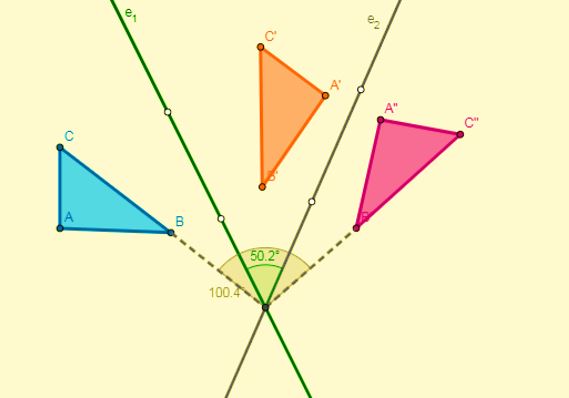
Por reflexión o simetría

Son aquellas transformaciones que invierten los puntos y figuras del plano. Esta inversión puede ser con respecto a un punto o también puede ser con respecto a una recta.

En otras palabras, en este tipo de transformación cada punto de la figura original se asocia a otro punto (imagen) de la figura homóloga, de tal forma que el punto y su imagen se encuentran a la misma distancia de una recta llamada eje de simetría.

Así, la parte izquierda de la figura será un reflejo de la parte derecha, sin cambiar su forma ni sus dimensiones. La simetría transforma una figura en otra igual aunque en sentido inverso, como se puede observar en la siguiente imagen:

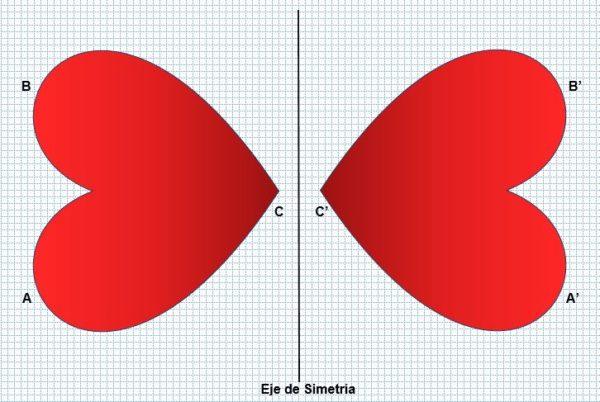
La simetría está presente en muchos aspectos, como en algunas plantas (girasoles), animales (pavo real) y fenómenos naturales (copos de nieve). El ser humano la refleja en su rostro, lo cual es considerado como un factor de belleza. La reflexión o simetría puede ser de dos tipos:

Simetría central

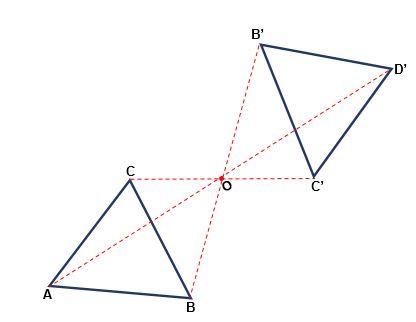
Es aquella transformación que ocurre con respecto a un punto, en la que la figura puede cambiar su orientación. Cada punto de la figura original y su imagen se encuentran a la misma distancia de un punto O, llamado centro de simetría. La simetría es central cuando:

• Tanto el punto como su imagen y centro pertenecen a una misma recta.
• Con una rotación de 180^o de centro O se obtiene una figura igual a la original.
• Los trazos de la figura inicial son paralelos con los trazos de la figura formada.
• El sentido de la figura no cambia, siempre será en sentido horario.

Esta transformación ocurre respecto al eje de simetría, donde cada punto de la figura inicial se asocia a otro punto de la imagen y estos se encuentran a la misma distancia del eje de simetría. La simetría es axial cuando:

• El segmento que une un punto con su imagen es perpendicular a su eje de simetría.
• Las figuras cambian de sentido respecto al giro o sentido horario.
• Al dividir la figura con una recta central (eje de simetría), una de las mitades resultantes coincide completamente con otra de las mitades.

Composición

Una composición de transformaciones isométricas se refiere a la aplicación sucesiva de transformaciones isométricas sobre una misma figura.

Composición de una traslación

La composición de dos traslaciones tiene como resultado otra traslación. Cuando se realiza sobre el plano, en el eje horizontal (x) solo cambian las coordenadas de ese eje, mientras que las coordenadas del eje vertical (y) se mantienen iguales, y viceversa.

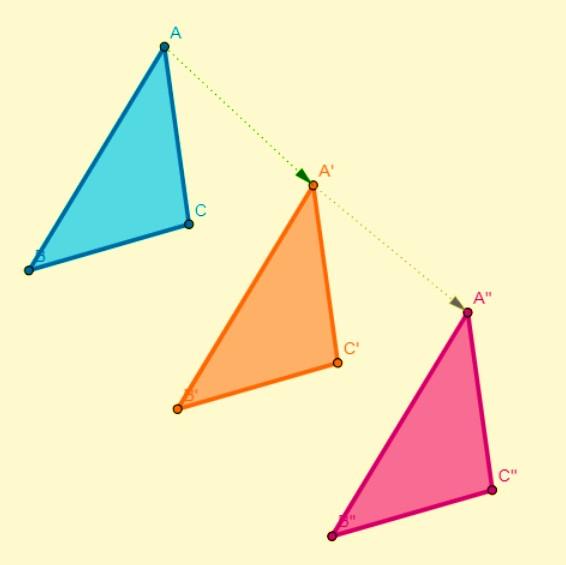
Composición de una rotación

La composición de dos giros con el mismo centro tiene como resultado otro giro, que posee el mismo centro y cuya amplitud será la suma de las amplitudes de los dos giros.

Si el centro los giros tiene distinto centro, el corte de la mediatriz de dos segmentos de puntos semejantes será el centro de giro.

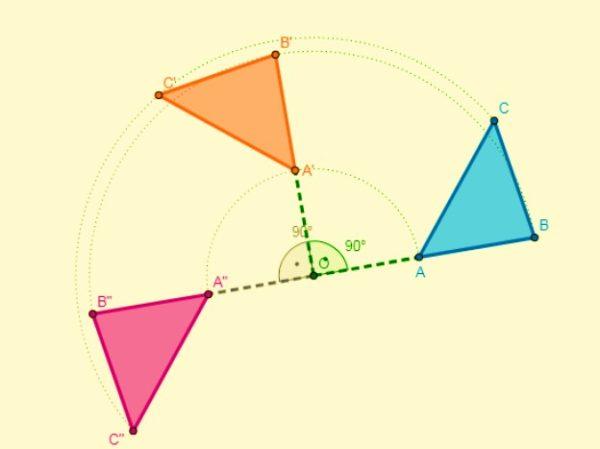
Composición de una simetría

En este caso, la composición va a depender de cómo sea aplicada:

• Si se aplica la misma simetría dos veces, el resultado será una identidad.
• Si se aplican dos simetrías con respecto a dos ejes paralelos el resultado será una traslación, y su desplazamiento es el doble de la distancia de esos ejes:

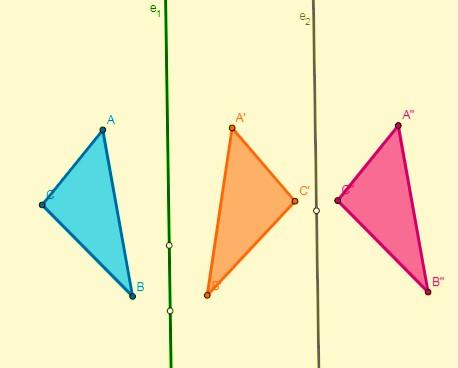
• Si se aplican dos simetrías con respecto a dos ejes que se cortan en el punto O (centro), se obtendrá una rotación con centro en O y su ángulo será el doble del ángulo que forman los ejes: