Biología matemática: historia, objeto de estudio, aplicaciones
La biología matemática o la biomatemática es una rama de la ciencia que se encarga del desarrollo de modelos numéricos que consigan simular distintos fenómenos naturales relacionados con los seres vivos; es decir, implica el uso de herramientas matemáticas para estudiar los sistemas naturales o biológicos.
Como puede entenderse de su nombre, la biomatemática es un área interdisciplinaria, que se encuentra en la intersección de conocimientos entre la biología y la matemática. Un ejemplo sencillo de esta disciplina podría incluir el desarrollo de métodos estadísticos para resolver problemas en el área de la genética o de la epidemiología, por nombrar algunas.
En esta área del conocimiento es normal que los resultados matemáticos surjan de problemas biológicos o sean empleados para resolverlos, no obstante, algunos investigadores han conseguido resolver problemas matemáticos en base a la observación de fenómenos biológicos, por lo que no se trata de una relación unidireccional entre ambos campos de la ciencia.
De lo anterior puede asegurarse que un problema matemático es el fin para el cual se emplean herramientas biológicas y viceversa; que un problema biológico es el fin para el cual se emplean las muy variadas herramientas matemáticas.
En la actualidad, el campo de la biología matemática crece a pasos acelerados y es considerado una de las más modernas y emocionantes aplicaciones de las matemáticas. Tiene gran utilidad no solo en la biología, sino en las ciencias biomédicas y en el campo de la biotecnología.
Índice del artículo
- 1 Historia de la biomatemática
- 2 Objeto de estudio de la biología matemática
- 3 Aplicaciones
- 4 Referencias
La matemática y la biología son dos ciencias con multiplicidad de aplicaciones. Las matemáticas son quizá tan antiguas como la cultura occidental, su origen se remonta a muchos años antes de Cristo y su utilidad ha sido demostrada desde entonces para gran cantidad de aplicaciones.
La biología como ciencia, sin embargo, es bastante más reciente, pues su conceptualización no ocurrió sino hasta principios del siglo XIX gracias a la intervención de Lamarck, por los años 1800.
La relación de los conocimientos matemáticos y biológicos es estrecha desde los primeros tiempos de las civilizaciones, puesto que el asentamiento de los pueblos nómadas tuvo lugar gracias al descubrimiento de que la naturaleza podía ser explotada sistemáticamente, lo que obligatoriamente tuvo que haber involucrado las primeras nociones matemáticas y biológicas.
En sus principios, las ciencias biológicas eran consideradas “artesanales”, puesto que se referían principalmente a actividades populares como la agricultura o la ganadería; entretanto las matemáticas descubrían la abstracción y tenían aplicaciones inmediatas un tanto distantes.
La confluencia entre la biología y la matemática se remonta, tal vez, a los siglos XV y XVI, con el advenimiento de la fisiología, que es una ciencia que agrupa conocimientos, clasificándolos, ordenándolos y sistematizándolos haciendo uso de herramientas matemáticas cuando es necesario.
Fue Thomas Malthus, un economista contemporáneo con Lamarck, quien sentó el precedente para el comienzo de la biología matemática, ya que fue el primero en postular un modelo matemático para explicar la dinámica poblacional en función de los recursos naturales.
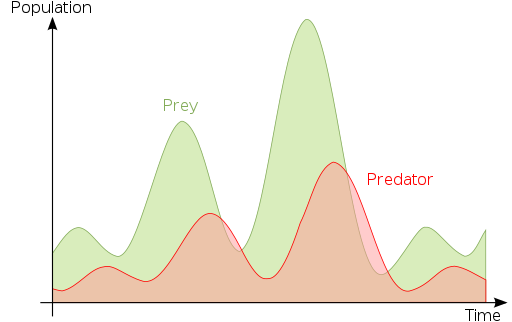
Los planteamientos de Malthus fueron posteriormente más desarrollados y elaborados, y hoy en día son parte del fundamento de los modelos ecológicos que se emplean para explicar la relación entre los depredadores y sus presas, por ejemplo.

La biología matemática es una ciencia que resulta de la integración de diferentes herramientas matemáticas con datos biológicos, experimentales o no, que busca aprovechar la “potencia” de los métodos matemáticos para explicar de mejor manera el mundo de los seres vivos, de sus células y de sus moléculas.
Sin importar el grado de complejidad tecnológica involucrado, la biología matemática consiste en la “simple” consideración de que existe una analogía entre dos procesos, a saber:
– La compleja estructura de un ser vivo es el resultado de la aplicación de operaciones sencillas de “copiado” y “corte y empalme” o “splicing” (por ejemplo) a una información inicial que está contenida en una secuencia de ADN (ácido desoxirribonucleico).
– El resultado f (ω) de la aplicación de una función computable a un arreglo w puede ser obtenido al aplicar una combinación de funciones básicas simples a w.
El campo de la biología matemática aplica áreas de la matemática como el cálculo, las teorías de probabilidades, la estadística, el álgebra lineal, la geometría algebraica, la topología, las ecuaciones diferenciales, los sistemas dinámicos, la combinatoria y la teoría de codificación.
Recientemente esta disciplina ha sido muy explotada para el análisis cuantitativo de distintos tipos de datos, pues las ciencias biológicas se han dedicado a producir grandes masas de datos de los cuales puede extraerse valiosa información.
De hecho, muchos investigadores consideran que la gran explosión de datos biológicos “creó” la necesidad de desarrollar nuevos y más complejos modelos matemáticos para su análisis, así como algoritmos computacionales y métodos estadísticos considerablemente más complejos.
Una de las aplicaciones más significativas de la biología matemática tiene que ver con el análisis de secuencias de ADN, pero esta ciencia también está implicada en el modelado de epidemias y en el estudio de la propagación de señales nerviosas.
Ha sido empleada para el estudio de procesos neurológicos como la enfermedad de Parkinson, el Alzheimer y la esclerosis lateral amiotrófica, por ejemplo.
Es de suma utilidad para el estudio de los procesos evolutivos (teorizaciones) y para el desarrollo de modelos que expliquen la relación de los seres vivos entre sí y con su entorno, es decir, para planteamientos ecológicos.
El modelado y la simulación de distintos tipos de cánceres también es un buen ejemplo de las múltiples aplicaciones que tiene la biología matemática hoy en día, especialmente en lo que respecta a la simulación de las interacciones entre poblaciones celulares.
La biomatemática también está muy avanzada en el área de neurociencia computacional, en los estudios de dinámicas poblacionales y de filogenómica y genómica en general.
En esta última rama de la genética ha sido de gran relevancia, pues se trata de una de las áreas con mayor crecimiento en los últimos años, ya que la tasa de obtención de datos es sumamente alta, lo que amerita de nuevas y mejores técnicas para su procesamiento y análisis.
- Andersson, S., Larsson, K., Larsson, M., & Jacob, M. (Eds.). (1999). Biomathematics: mathematics of biostructures and biodynamics. Elsevier.
- Elango, P. (2015). The role of Mathematics in Biology.
- Friedman, A. (2010). What is mathematical biology and how useful is it. Notices of the AMS, 57(7), 851-857.
- Hofmeyr, J. H. S. (2017). Mathematics and biology. South African Journal of Science, 113(3-4), 1-3.
- Kari, L. (1997). DNA computing: arrival of biological mathematics. Mathematical Intelligencer, 19(2), 9-22.
- Pacheco Castelao, J. M. (2000). ¿Qué es la biología matemática?
- Reed, M. C. (2004). Why is mathematical biology so hard? Notices of the AMS, 51(3), 338-342.
- Ulam, S. M. (1972). Some ideas and prospects in biomathematics. Annual review of biophysics and bioengineering, 1(1), 277-292.
