Pirámide hexagonal: características, cómo hacerla, ejemplos
¿Qué es una pirámide hexagonal?
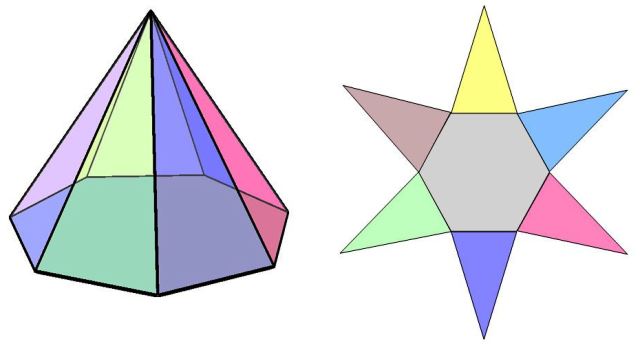
Una pirámide hexagonal es una figura geométrica en tres dimensiones, cuya base es un hexágono (polígono de seis lados) y que además tiene seis caras de forma triangular, las cuales se juntan a cierta altura de la base, en un punto llamado ápice o vértice.
En total, la pirámide hexagonal tiene siete caras si se cuenta la base más las caras laterales, por eso también es un poliedro con forma de heptaedro, palabra derivada del idioma griego (“hepta” significa siete).
Si los triángulos que forman los lados son isósceles, es decir, tienen dos lados iguales y uno diferente, se trata de una pirámide recta. Y si, aparte de eso, el hexágono de la base es regular, entonces se trata de una pirámide hexagonal regular, como la que se muestra en la figura 1.
Cuando el hexágono de la base no es regular, o los triángulos que forman las caras no son isósceles, se tiene una pirámide hexagonal oblicua.
Características de la pirámide hexagonal
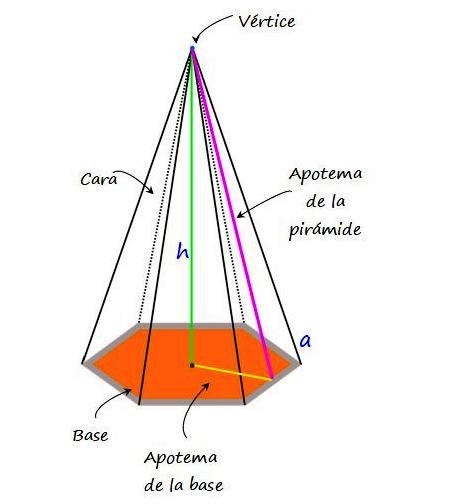
Las principales características y elementos de la pirámide hexagonal son los siguientes:
–Base, es un hexágono que puede ser regular o irregular.
–Caras, tienen forma de triángulo y en total de 6.
–Vértice o ápicede la pirámide, punto de coincidencia de las seis caras triangulares.
–Arista, segmento donde coinciden dos de las caras de la pirámide. Las aristas laterales son los segmentos de coincidencia de las caras laterales, mientras que las aristas de la base son los segmentos donde coinciden un lado del hexágono y un lado del triángulo adyacente. En la figura 2, la arista se denota mediante la letra “a”.
–Altura, denotada como “h”, es la distancia medida desde el vértice hasta la base de la pirámide.
–Apotema de la pirámide, segmento que une al vértice con el punto medio de un lado de la base.
–Apotema de la base, se define únicamente cuando el hexágono es regular. Consiste en un segmento que une al centro del hexágono con el centro de uno de sus lados.
Fórmulas para el área y el volumen
El área superficial A de la pirámide hexagonal, ya sea regular o irregular, se calcula sumando las áreas de las caras laterales y el área de la base hexagonal:
A = Abase + ∑Acaralateral
En la fórmula, el símbolo “∑” representa una suma, para indicar de forma resumida la suma las seis áreas de las caras laterales.
Para la pirámide hexagonal regular existe una fórmula para hallar el área:
A = 3L∙ (apbase + appirámide)
Donde:
- L es una arista de la base (el lado del hexágono).
- apbase es la apotema de la base
- appirámide es la apotema de la pirámide.
Si la pirámide no es regular, ya sea porque la base no es un hexágono regular o porque la pirámide es oblicua, es preciso calcular por separado las áreas de cada una y después sumar.
La pirámide hexagonal regular también dispone de una fórmula para el volumen:
V = L∙ apbase∙ h
Aquí “h” representa la altura de la pirámide.
Y si la pirámide hexagonal no es regular, existe una fórmula general, aplicable a todas las pirámides, para calcular su volumen:
V = ⅓∙ Abase ∙ h
Ejemplo numérico
Para la pirámide hexagonal regular cuyas dimensiones son:
Apotema de la base: 4 cm
Longitud de la arista de la base: 7 cm
Apotema de la pirámide: 15 cm
Altura: 10 cm
Calcular los siguientes:
a) Área de la base hexagonal.
b) Área superficial de la pirámide.
c) El volumen
Solución a
El área de un hexágono regular es:
A = ½ (Perímetro × apotema) = ½ (6L× apbase)
A = 3L∙ apbase = 3×7cm × 4cm = 84cm2
Solución b
A = 3L∙ (apbase + appirámide) = 3L∙ apbase + 3L∙ appirámide = 84cm2 + (3×7cm×15cm) = 399 cm2.
Solución c
El volumen se puede hallar mediante la fórmula general:
V = ⅓∙ Abase ∙ h = ⅓∙ 84cm2 ∙10cm = 280 cm3
¿Cómo hacer una pirámide hexagonal?
Materiales
- Papel, cartulina o cartón.
- Regla y escuadra
- Lápiz de grafito y marcadores de colores
- Tijera
- Pegamento para manualidades.
Procedimiento
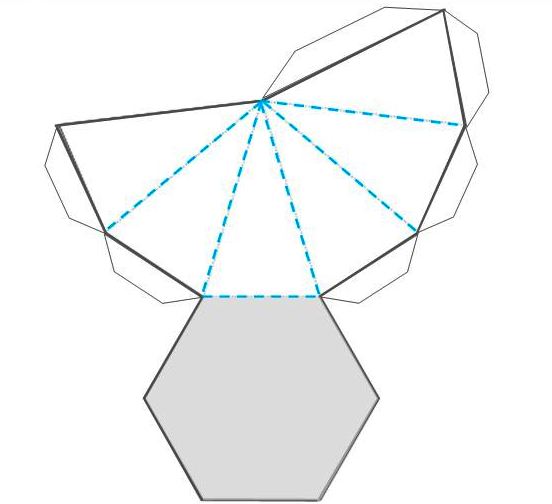
- Trasladar la plantilla mostrada a continuación, a la escala deseada, sobre el cartón o la cartulina, con ayuda del lápiz de grafito, la regla y la escuadra. Otra opción es copiar la figura en un archivo tipo documento o dibujo editable y agrandarla hasta que tenga las dimensiones deseadas.
- Una vez que la plantilla se ha trasladado al papel o la cartulina, se debe recortar con mucho cuidado.
- Ahora doblar por las líneas punteadas para dar forma a la pirámide, asegurándose de que los lados encajen correctamente.
- Doblar también las pestañas, verificar que encajan bien y seguidamente agregarles pegamento, presionándolas con cuidado para que queden en su sitio, dando forma a la figura.
- Decorar a gusto la pirámide con los marcadores de colores.
Ejemplos de pirámides hexagonales
De acuerdo al hexágono de la base, las pirámides hexagonales pueden ser:
–Convexas, si todos los ángulos internos del hexágono son menores a 180º.
–Cóncavas, si uno o más de los ángulos internos del hexágono mide más de 180º.
La pirámide hexagonal regular de la figura 1 es convexa, ya que todos los ángulos internos de la base miden menos de 180º. Para ser exactos, los ángulos internos del hexágono regular miden todos 120º.
De acuerdo a esto, la forma de las pirámides hexagonales varían, como se muestra seguidamente.
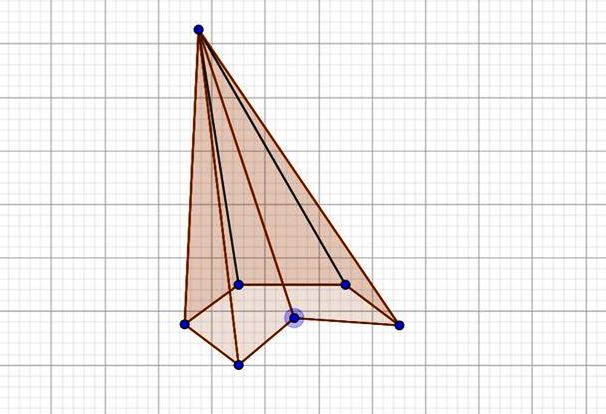
Pirámide hexagonal oblicua
En la imagen de la figura 4 se observa una pirámide hexagonal oblicua, cuya base es regular. Obsérvese el triángulo que conforma la cara en primer plano, es un triángulo con sus tres lados diferentes (triángulo escaleno), a diferencia de la pirámide en la figura 1, cuyas caras son triángulos isósceles. Si se traza una línea desde el vértice hasta el centro del hexágono, resulta estar inclinada respecto a la vertical.
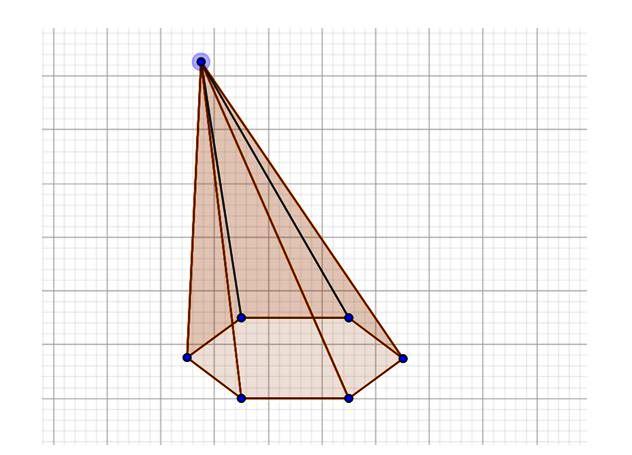
Pirámide hexagonal cóncava y oblicua
La base de esta pirámide hexagonal contiene un ángulo interno cuya medida es mayor a 180º, por lo tanto se trata de una pirámide cóncava, además de ser oblicua.