Proyección cónica cartográfica: características, ventajas, desventajas
La proyección cónica cartográfica se caracteriza por proyectar los puntos de una superficie esférica sobre la superficie de un cono, cuyo vértice se ubica sobre el eje que pasa por los polos y es tangente o secante a la esfera. El cono es una superficie que se puede abrir en un plano, formando un sector angular y sin deformar las líneas proyectadas sobre él.
El matemático Johann Heinrich Lambert (1728 – 1777) fue quién ideó esta proyección, apareciendo por primera vez en su libro Freye Perspective (1759), donde recopilaba varias teorías y reflexiones acerca de las proyecciones.
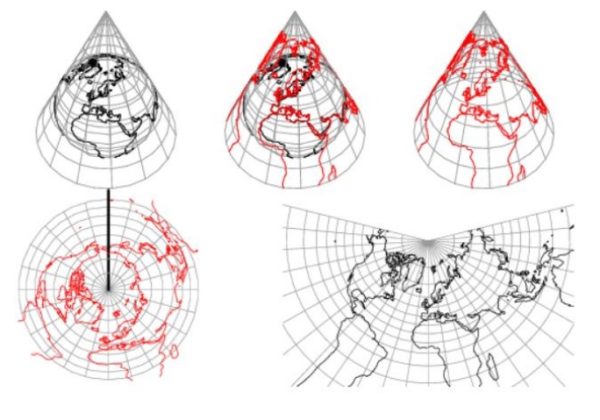
En las proyecciones cónicas de la superficie terrestre, los meridianos pasan a ser líneas radiales centradas en el vértice, con igual espaciamiento angular y los paralelos terrestres pasan a ser arcos circulares concéntricos al vértice.
En la figura 1 se pone de manifiesto que la proyección cónica no permite representar ambos hemisferios. Además, se observa claramente que las distancias se distorsionan lejos de los paralelos que interceptan al cono.
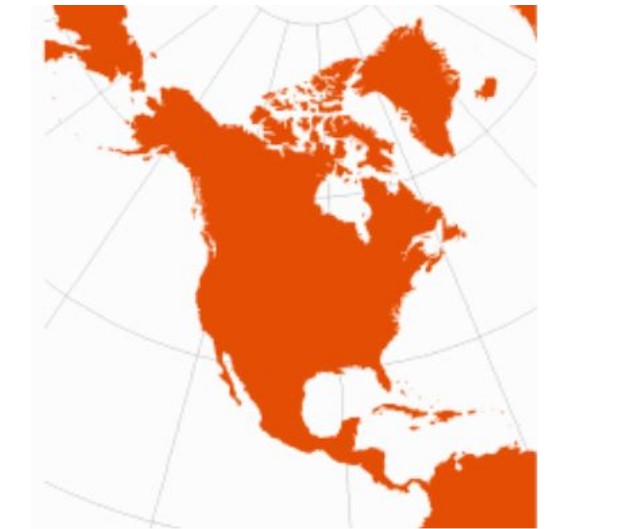
Debido a estas razones, este tipo de proyección se usa para representar regiones de latitud media, extensas de este a oeste y de menor extensión norte-sur. Tal es el caso de la región continental de los Estados Unidos.
Índice del artículo
La Tierra se puede aproximar a una esfera de 6378 km de radio, considerando que todas las masas terrestres y acuáticas están sobre esa gran esfera. Se trata de convertir esta superficie, que recubre un objeto en tres dimensiones, como lo es una esfera, en otro objeto en dos dimensiones: un mapa plano. Esto trae el inconveniente de que la superficie curva se distorsiona, al querer proyectarla sobre el plano.
Las proyecciones cartográficas, como la proyección cónica, tratan de solventar este problema con la menor pérdida de exactitud posible. De allí que existan varias opciones para hacer una proyección, según las características que se quieran resaltar.
Entre estas características importantes están las distancias, la superficie, los ángulos y más. La mejor forma de conservarlas a todas es representando la Tierra en 3D a escala. Pero esto no siempre es práctico.
Transportar un globo terráqueo a todos lados no es fácil, ya que ocupa volumen. Tampoco se puede ver toda la superficie de la Tierra a la vez, y es imposible reproducir todos los detalles en un modelo a escala.
Podemos imaginar que el planeta es una naranja, pelamos la naranja y extendemos la cáscara sobre la mesa, procurando reconstruir la imagen de la superficie de la naranja. Está claro que en el proceso se perderá mucha información.
Las opciones de proyección son las siguientes:
– Proyectar sobre un plano o
– Sobre un cilindro, que se puede desarrollar como un plano rectangular.
– Finalmente sobre un cono.
El sistema de proyección cónica tiene la ventaja que es exacto sobre los paralelos elegidos para interceptar el cono de proyección.
Además, mantiene prácticamente intacta la orientación a lo largo de los meridianos, aunque puede distorsionar un poco la escala a lo largo de los mismos para las latitudes lejanas a los paralelos estándar o de referencia. Por eso es apropiada para representar países muy extensos o continentes.
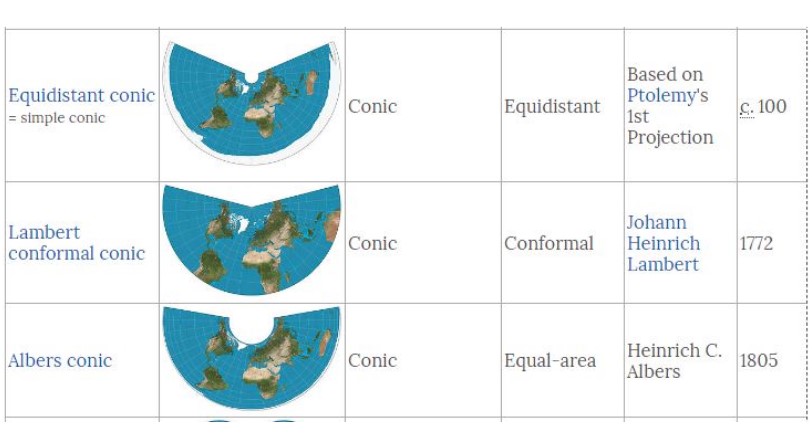
Es el sistema de proyección cónico usado originalmente por Ptolomeo, geógrafo griego que vivió entre los años 100 a 170 d. C. Posteriormente en 1745 fue mejorado.
Es usado frecuentemente en los atlas de las regiones con latitudes intermedias. Es adecuada para mostrar zonas con unos cuantos grados de latitud, y que pertenezcan a uno de los hemisferios ecuatoriales.
En esta proyección, las distancias son verdaderas a lo largo de los meridianos y en los dos paralelos estándar, es decir los paralelos elegidos para interceptar con el cono de proyección.
En la proyección cónica equidistante, un punto sobre la esfera se extiende radialmente hasta su intersección con el cono tangente o secante, tomando como centro de proyección el centro de la esfera.
Desventajas
La principal desventaja de la proyección cónica es que no es aplicable a las regiones ecuatoriales.
Además, la proyección cónica no es apropiada para cartografiar regiones de gran tamaño, sino más bien zonas particulares, como por ejemplo Norteamérica.
Usa dos paralelos estándar y preserva el área, aunque no la escala y la forma. Este tipo de proyección cónica fue presentada por H. C. Albers en el año 1805.
Todas las áreas en el mapa son proporcionales a las correspondientes en la Tierra. En regiones limitadas, las direcciones son relativamente precisas. Las distancias corresponden a las de la superficie esférica sobre los paralelos estándar.
En los Estados Unidos se usa este sistema de proyección para los mapas que muestran los límites de los estados de la Unión, para los que se eligen como paralelos estándar el 29,5º N y 45,5º N resultando como error máximo de escala 1,25%.
Los mapas hechos con esta proyección no conservan los ángulos correspondientes a los de la esfera, y tampoco conserva la perspectiva ni la equidistancia.
Fue propuesta en 1772 por el matemático y geógrafo suizo del mismo nombre. Su principal característica es que usa un cono tangente o secante a la esfera y la proyección conserva invariante los ángulos. Estas cualidades la hacen muy útil en las cartas aeronáuticas de navegación.
El servicio geológico de los Estados Unidos (USGS) emplea la proyección cónica de Lambert. En esta proyección, las distancias son verdaderas a lo largo de los paralelos estándar.
En la proyección cónica de Lambert las direcciones se mantienen razonablemente precisas. Las áreas y formas se distorsionan poco en posiciones cercanas a los paralelos estándar, pero la alteración de forma y área aumenta con la separación a ellos.
Debido a que el objetivo de esta proyección es mantener direcciones y ángulos iguales a los originales sobre la esfera o elipsoide, no hay un método geométrico de obtenerla, a diferencia de la proyección equidistante de Ptolomeo.
Más bien es un método de proyección analítico, basado en fórmulas matemáticas.
Los mapas base de el USGS para los 48 estados continentales usan como paralelos estándar 33ºN y 45ºN, arrojando un error máximo en los mapas del 2,5%.
Para las cartas de navegación en Alaska, los paralelos base usados son 55ºN y 65ºN. En cambio, el atlas nacional del Canadá usa 49ºN y 77ºN.
- Geohunter. The Lambert Conformal Conic projection. Recuperado de: geo.hunter.cuny.edu
- Gisgeography. Conic Projection: Lambert, Albers and Polyconic. Recuperado de: gisgeography.com
- Gisgeography. What are Map Projections? Recuperado de: gisgeography.com
- USGS. Map projections. Recuperado de: icsm.gov.au
- Weisstein, Eric W. “Albers Equal-Area Conic Projection.” Recuperado de: mathworld.wolfram.com
- Weisstein, Eric W. “Conic Projection” Recuperado de: mathworld.wolfram.com
- Weisstein, Eric W. “Lambert Conformal Conic Projection” Recuperado de: mathworld.wolfram.com
- Wikipedia. List of map projections. Recuperado de: en.wikipedia.com
