Matriz inversa: cálculo y ejercicio resuelto
La matriz inversa de una matriz dada, es la matriz que multiplicada por la original da como resultado la matriz identidad. La matriz inversa es útil para resolver sistemas de ecuaciones lineales, de allí la importancia de saber calcularla.
Las matrices son de gran utilidad en física, ingeniería y matemáticas, ya que son una herramienta compacta para resolver problemas complejos. La utilidad de las matrices se potencia cuando estas son invertibles y además se conoce su inversa.
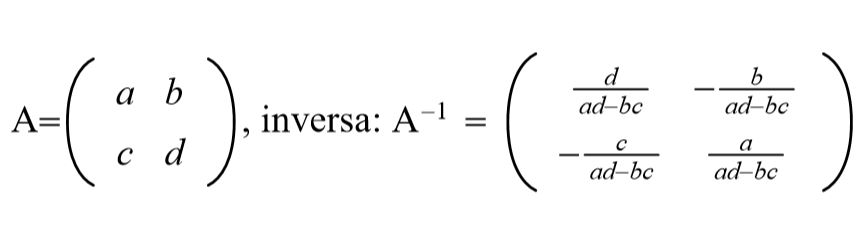
En los campos de procesamiento gráfico, Big Data, Data Mining, Machine Learning y otros se usan algoritmos eficientes y rápidos para evaluar la matriz inversa de matrices nxn con n muy grande, en el orden de los miles o los millones.
Para ilustrar el uso de la matriz inversa en el manejo de sistema de ecuaciones lineales comenzaremos con el caso más simple de todos: matrices 1×1.
El caso más sencillo: se considera una ecuación lineal de una sola variable: 2 x = 10.
La idea es encontrar el valor de x, pero se hará “matricialmente”.
La matriz M = (2) que multiplica al vector (x) es una matriz 1×1 que da como resultado el vector (10):
M (x) = (10)
La inversa de la matriz M se denota por M-1.
La forma general de escribir este “sistema lineal” es:
M X = B, donde X es el vector (x) y B es el vector (10).
Por definición, la matriz inversa es aquella que multiplicada por la matriz original da como resultado la matriz identidad I:
M-1 M = I
En el caso considerado, la matriz M-1 es la matriz (½), es decir M-1 = (½) ya que M-1 M = (½)(2) = (1) = I
Para encontrar el vector incógnita X = (x), en la ecuación planteada, se multiplica ambos miembros por la matriz inversa:
M-1 M (x) = M-1 (10)
(½) (2) (x) = (½) (10)
(½ 2) (x) = ( ½ 10 )
(1) (x) = (5)
(x) = (5)
Se ha llegado a una igualdad de dos vectores, los cuales son iguales solo cuando sus elementos correspondientes son iguales, es decir x = 5.
Cálculo de la inversa de una matriz
Lo que motiva el cálculo de la matriz inversa es encontrar un método universal para la solución de sistemas lineales como el siguiente sistema 2×2:
x – 2 y = 3
-x + y = -2
Siguiendo los pasos del caso 1×1, estudiado en el apartado anterior, escribimos el sistema de ecuaciones en forma matricial:
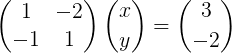
Note que este sistema se escribe en notación vectorial compacta de la siguiente manera:
M X = B
donde
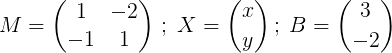
El próximo paso es encontrar la inversa de M.
Método 1: mediante eliminación gaussiana
Se aplicará el método de eliminación de Gauss. El cual consiste en hacer operaciones elementales sobre las filas de la matriz, estas operaciones son:
– Multiplicar una fila por un número no nulo.
– Sumar o resta a una fila otra fila, o el múltiplo de otra fila.
– Intercambiar las filas.
El objetivo es, mediante estas operaciones, convertir la matriz original en la matriz identidad.
A la par que se realiza esto, en la matriz M se aplican exactamente las mismas operaciones a la matriz identidad. Cuando después de varias operaciones en las filas M se transforme a la matriz unitaria, entonces la que originalmente era la unitaria se transformará en la matriz inversa de M, es decir M-1.
1- Comenzamos el proceso escribiendo la matriz M y a su lado la matriz unitaria:
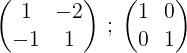
2- Sumamos las dos filas y el resultado lo ponemos en la segunda fila, de esta manera obtenemos un cero en el primer elemento de la segunda fila:
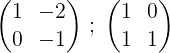
3- Multiplicamos la segunda fila por -1 para obtener 0 y 1 en la segunda fila:
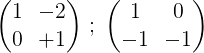
4- Se multiplica la primera fila por ½ :

5- Se suma la segunda y la primera y el resultado se coloca en la primera fila:
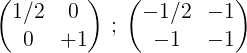
6- Ya para finalizar el proceso, se multiplica la primera fila por 2 para obtener en la primera la matriz identidad y en la segunda la matriz inversa de la matriz original M:
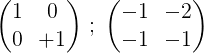
Es decir:
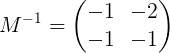
Solución del sistema
Una vez obtenida la matriz inversa se procede a resolver el sistema de ecuaciones mediante la aplicación de la matriz inversa en ambos miembros de la ecuación vectorial compacta:
M-1M X = M-1B
X = M-1B
Que en forma explícita queda así:
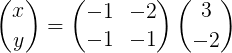
Luego se efectúa la multiplicación matricial para obtener el vector X:
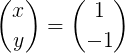
Método 2: mediante matriz adjunta
En este segundo método la matriz inversa se calcula partiendo de la matriz adjunta de la matriz original A.
Supongamos una matriz A dada por:

donde ai,j es el elemento de la fila i y la columna j de la matriz A.
La adjunta de la matriz A se denominará Adj(A) y sus elementos son:
adi,j = (-1)(i+j) ¦Ai,j¦
donde Ai,j es la matriz menor complementaria que se obtiene al eliminar la fila i y la columna j de la matriz original A. Las barras ¦ ¦ indican que se calcula el determinante, es decir ¦Ai,j¦ es el determinante de la matriz menor complementaria.
Fórmula de la matriz inversa
La fórmula para hallar la matriz inversa partiendo de la matriz adjunta de la matriz original es la siguiente:
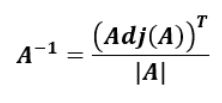
Es decir, la matriz inversa de A, A-1, es la transpuesta de la adjunta de A dividida entre el determinante de A.
La transpuesta ATde una matriz A es la que se obtiene al intercambiar filas por columnas, es decir, la primera fila pasa a ser primera columna y la segunda fila a segunda columna y así sucesivamente hasta completar la n filas de la matriz original.
Ejercicio resuelto
Sea la matriz A la siguiente:
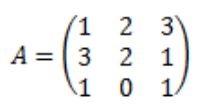
Se calculan todos y cada uno de los elementos de la matriz adjunta de A: Adj(A)
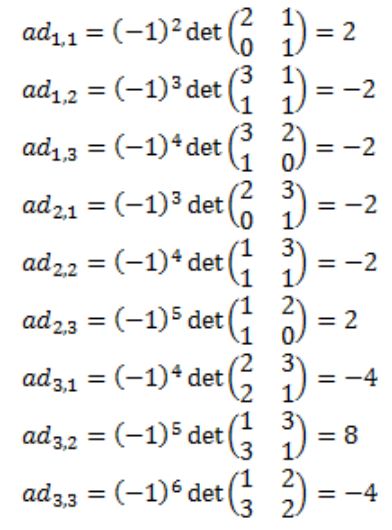
Resultando que la matriz adjunta de A, Adj(A) es la siguiente:
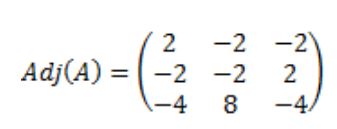
Luego se calcula el determinante de la matriz A, det(A):
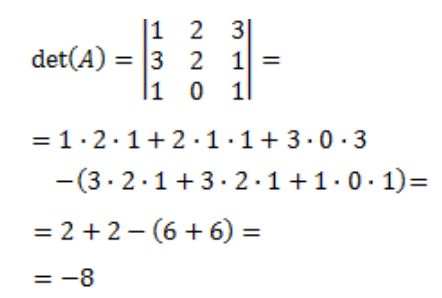
Finalmente se obtiene la matriz inversa de A:
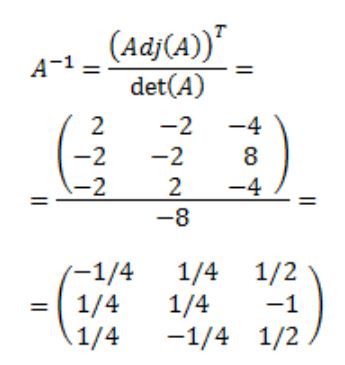
Referencias
- Anthony Nicolaides (1994) Determinants & Matrices. Pass Publication.
- Awol Assen (2013) A Study on the Computation of the Determinants of a 3×3
- Casteleiro Villalba M. (2004) Introducción al álgebra lineal. ESIC Editorial.
- Dave Kirkby (2004) Maths Connect. Heinemann.
- Jenny Olive (1998) Maths: A Student’s Survival Guide. Cambridge University Press.
- Richard J. Brown (2012) 30-Second Maths: The 50 Most Mind-Expanding Theories in Mathematics. Ivy Press Limited.
- Matrix. Lap Lambert Academic Publishing.
