Triángulo escaleno: qué es, características, elementos, ejemplos

¿Qué es un triángulo escaleno?

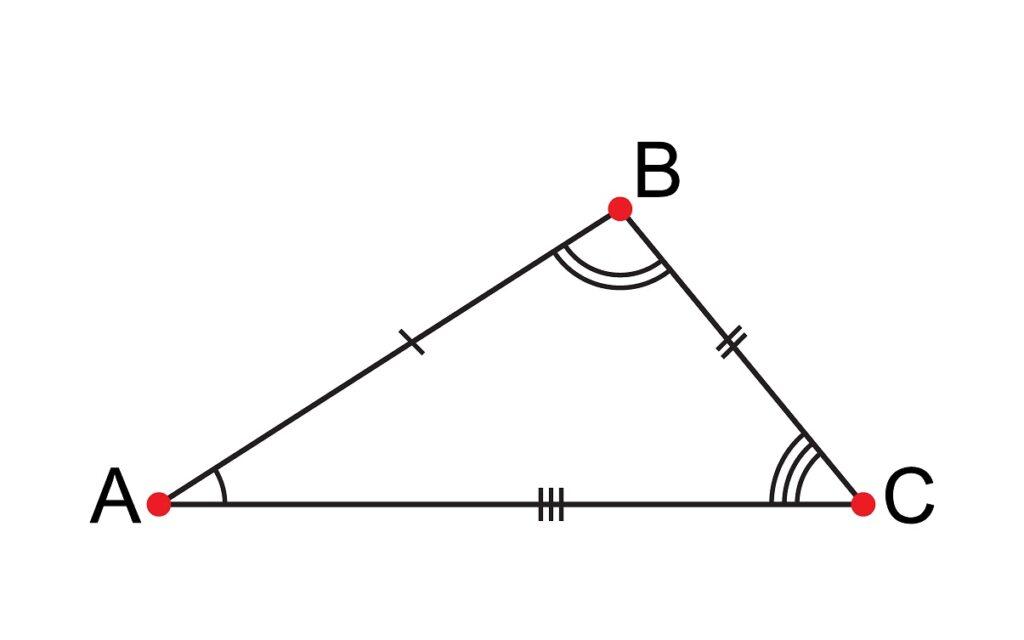
Un triángulo escaleno es un polígono de tres lados, donde todos tienen diferentes medidas o longitudes; por esa razón le fue dado el nombre de escaleno, que en latín significa desigual.

Los triángulos son polígonos considerados como los más simples en la geometría, porque están formados tres lados, tres ángulos y tres vértices. En el caso del triángulo escaleno, por tener todos los lados diferentes, implica que sus tres ángulos también lo serán.

Características de los triángulos escalenos

Los triángulos escalenos son polígonos simples debido a que ninguno de sus lados o ángulos tiene la misma medida, a diferencia de los triángulos isósceles y equiláteros.

Debido a que todos sus lados y ángulos poseen medidas diferentes, estos triángulos son considerados polígonos convexos irregulares.

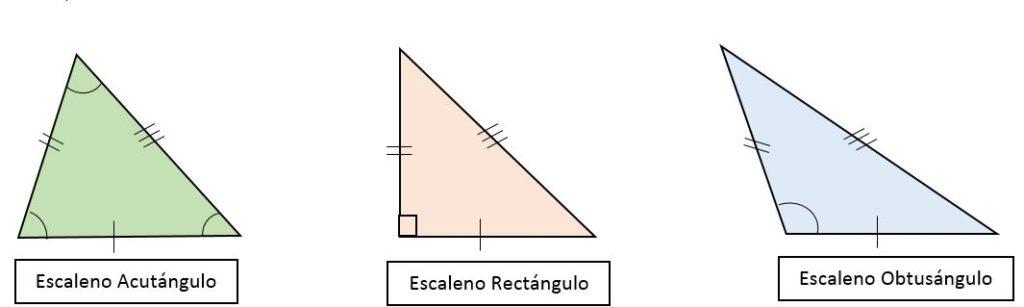
Según la amplitud de los ángulos internos, los triángulos escalenos se clasifican en:

• Triangulo rectángulo escaleno: todos sus lados son diferentes. Uno de sus ángulos es recto (90^o) y los otros son agudos y con diferentes medidas.
• Triángulo obtusángulo escaleno: todos sus lados son diferentes y uno de sus ángulos es obtuso (> 90^o).
• Triángulo acutángulo escaleno: todos sus lados son diferentes. Todos sus ángulos son agudos ( 90^o), con medidas diferentes.

Otra característica de los triángulos escalenos es que debido a la incongruencia de sus lados y ángulos, no posee eje de simetría.

Componentes/elementos

La mediana

Es una recta que sale desde el punto medio de un lado y llega al vértice opuesto. Las tres medianas concurren en un punto llamado baricentro o centroide.

La bisectriz

Es una semirrecta que divide cada ángulo en dos ángulos de igual medida. Las bisectrices de un triángulo concurren en punto llamado incentro.

La mediatriz

Es un segmento perpendicular al lado del triángulo, que tiene origen en la mitad de este. Existen tres mediatrices en un triángulo y concurren en un punto llamado circuncentro.

La altura 

Es la recta que va desde el vértice hasta el lado opuesto, y además esta recta es perpendicular a dicho lado. Todos los triángulos tienen tres alturas que coinciden en un punto llamado ortocentro.

Propiedades del triángulo escaleno

Los triángulos escalenos son definidos o identificados porque tienen varias propiedades que los representan, originadas de los teoremas propuestos por grandes matemáticos. Ellas son:

Ángulos internos

La suma de los ángulos internos es siempre igual a 180^o.

Suma de los lados

La suma de las medidas de dos lados siempre debe ser mayor que la medida del tercer lado, a + b > c.

Lados incongruentes

Todos los lados de los triángulos escalenos tienen diferentes medidas o longitudes; es decir, son incongruentes.

Ángulos incongruentes

Ya que todos los lados del triángulo escaleno son diferentes, sus ángulos también lo serán. Sin embargo, la suma de los ángulos internos siempre será igual a 180º, y en algunos casos, uno de sus ángulos puede ser obtuso o recto, mientras que en otros todos sus ángulos serán agudos.

Altura, mediana, mediatriz y bisectriz no son coincidentes

Como todo triángulo, el escaleno tiene diversos segmentos de rectas que lo componen, como lo son: altura, mediana, mediatriz y bisectriz.

Debido a la particularidad de sus lados, en este tipo de triángulo ninguna de estas rectas van a coincidir en una sola.

Ortocentro, baricentro, incentro y circuncentro no son coincidentes

Como la altura, mediana, bisectriz y mediatriz son representadas por diferentes segmentos de rectas, en un triángulo escaleno los puntos de encuentro –el ortocentro, baricentro incentro y circuncentro–, se encontrarán en diferentes puntos (es decir, no coinciden).

Dependiendo de si el triángulo es acutángulo, rectángulo u obtusángulo, el ortocentro tiene diferentes ubicaciones:

a. Si el triángulo es acutángulo, el ortocentro estará en el interior del triángulo.

b. Si el triángulo es rectángulo, el ortocentro coincidirá con el vértice del lado recto.

c. Si el triángulo es obtusángulo, el ortocentro estará en el exterior del triángulo.

Alturas relativas

Las alturas son relativas a los lados.

En el caso del triángulo escaleno, estas alturas tendrán diferentes medidas. Todo triángulo tiene tres alturas relativas y para calcularlas es usada la fórmula de Herón.

Cálculo de perímetro, área, altura y lados

¿Cómo calcular el perímetro?

El perímetro de un polígono es calculado mediante la suma de los lados.

Como en este caso el triángulo escaleno tiene todos sus lados con diferente medida, su perímetro será:

P = lado a + lado b + lado c.

¿Cómo calcular el área?

El área de los triángulos siempre se calcula con la misma fórmula, multiplicando la base por altura y dividiendo entre dos:

Área = (base _* h) ÷2

En algunos casos la altura del triángulo escaleno no es conocida, pero existe una fórmula que fue propuesta por el matemático Herón, para calcular el área conociendo la medida de los tres lados de un triángulo.

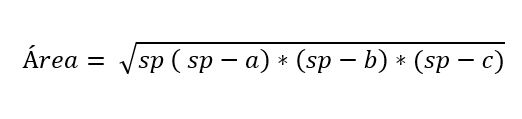
Donde:

• a, b y c representan a los lados del triángulo.
• sp corresponde al semiperímetro del triángulo, es decir, la mitad del perímetro:

sp = (a + b + c) ÷ 2

En el caso de que solo se tenga la medida de dos de los lados del triángulo y el ángulo que se forma entre estos, el área puede ser calculada aplicando las razones trigonométricas. Así se tiene que:

Área = (lado _* h) ÷2

Donde la altura (h) es el producto de un lado por el seno del ángulo opuesto. Por ejemplo, para cada lado, el área será:

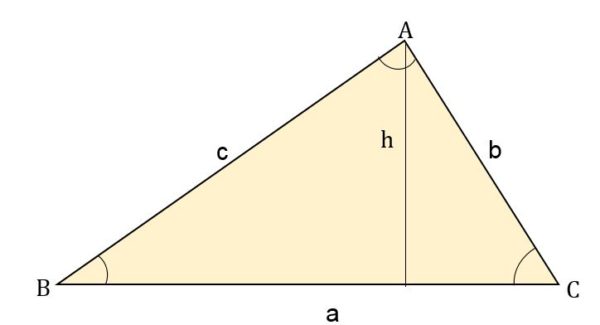
• Área = (b _* c _* sen A) ÷ 2
• Área = (a _* c _* sen B) ÷ 2.
• Área = (a _* b _* sen C) ÷ 2

¿Cómo calcular la altura?

Como todos los lados del triángulo escaleno son diferentes, no es posible calcular la altura con el teorema de Pitágoras.

A partir de la fórmula de Herón, que se basa en las medidas de los tres lados de un triángulo, puede ser calculada el área.

La altura puede ser despejada de la fórmula general del área:

El lado es sustituido por la medida del lado a, b o c.

Otra forma de calcular la altura cuando se conoce el valor de uno de los ángulos, es aplicando las razones trigonométricas, donde la altura va a representar a un cateto del triángulo.

Por ejemplo, cuando se conoce el ángulo opuesto a la altura, esta será determinada por el seno:

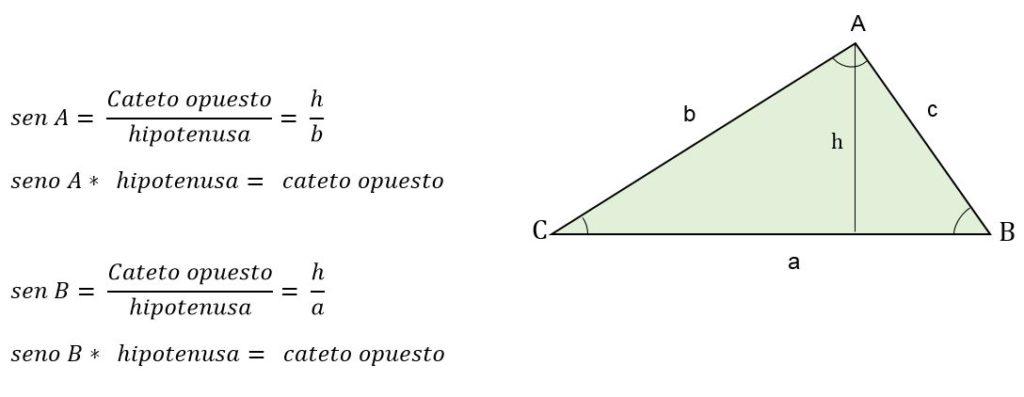
¿Cómo calcular los lados?

Cuando se tiene la medida de dos lados y el ángulo opuesto a estos, es posible determinar el tercer lado aplicando el teorema de los cosenos.

Por ejemplo, en un triángulo AB, se traza la altura relativa al segmento AC. De esa forma el triángulo es dividido en dos triángulos rectángulos.

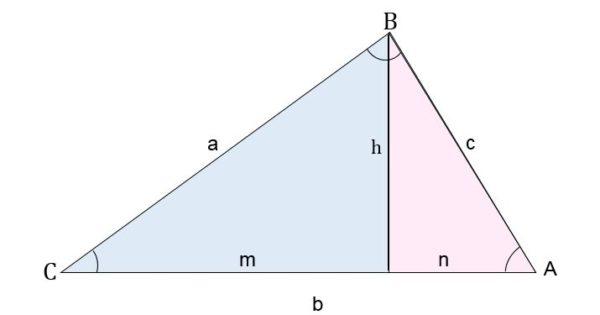
Para calcular el lado c (segmento AB), se aplica el teorema de Pitágoras para cada triángulo:

• Para el triángulo azul se tiene que:

c² = h² + m²

Como m = b – n, se sustituye:

c² = h² + b² (b – n)²

c² = h² + b² – 2bn + n².

• Para el triángulo rosa se tiene que:

h² = a² – n²

Se sustituye en la ecuación anterior:

c² = a² – n² + b² – 2bn + n²

c² = a² + b² – 2bn.

Sabiendo que n = a _* cos C, se sustituye en la ecuación anterior y se obtiene el valor del lado c:

c² = a² + b² – 2b_* a _* cos C.

Por la Ley de los cosenos, los lados pueden ser calculados como:

• a² = b² + c² – 2b_* c _* cos A.
• b² = a² + c² – 2a_* c _* cos B.
• c² = a² + b² – 2b_* a _* cos C.

Existen casos donde no se conocen las medidas de los lados del triángulo, sino su altura y los ángulos que se forman en los vértices. Para determinar el área en estos casos es necesario aplicar las razones trigonométricas.

Sabiendo el ángulo de uno de sus vértices, se identifican los catetos y se utiliza la razón trigonométrica que corresponda:

Por ejemplo, el cateto AB será opuesto para el ángulo C, pero adyacente al ángulo A. En función del lado o cateto correspondiente a la altura, se despeja el otro lado para obtener el valor de este.

Ejercicios resueltos

Primer ejercicio

Calcular el área y una altura del triángulo escaleno ABC, sabiendo que sus lados son:

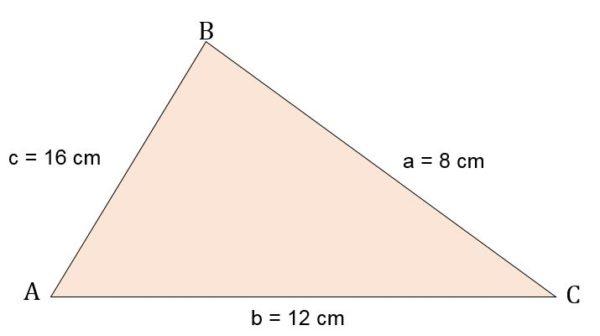
a = 8 cm.

b = 12 cm.

c = 16 cm.

Solución

Como dato son dadas las medidas de los tres lados del triángulo escaleno.

Debido a que no se tiene el valor de la altura, se puede determinar el área aplicando la fórmula de Herón.

Primero se calcula el semiperímetro:

sp = (a + b + c) ÷ 2

sp = ( 8 cm + 12 cm + 16 cm) ÷ 2

sp = 36 cm ÷ 2

sp = 18 cm.

Ahora se sustituyen los valores en la fórmula de Herón:

Conociendo el área puede ser calculada la altura relativa al lado b. A partir de la fórmula general, despejándola se tiene:

Área = (lado _* h) ÷ 2

46, 47 cm² = (12 cm _* h) ÷2

h = (2 _* 46,47 cm²) ÷ 12 cm

h = 92,94 cm² ÷ 12 cm

h = 7,75 cm.

Segundo ejercicio

Dado el triángulo escaleno ABC, cuyas medidas son:

• Segmento AB = 25 m.
• Segmento BC = 15 m.

En el vértice B se forma un ángulo de 50º. Calcular la altura relativa al lado c, perímetro y área de ese triángulo.

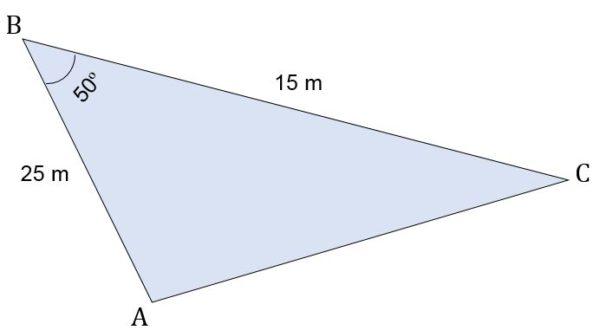
Solución

En este caso se tienen las medidas de dos lados. Para determinar la altura es necesario calcular la medida del tercer lado.

Como es dado el ángulo opuesto a los lados dados, es posible aplicar la ley de los cosenos para determinar la medida del lado AC (b):

b² = a² + c² – 2a_*c _* cos B

Donde:

a = BC = 15 m.

c = AB = 25 m.

b = AC.

B = 50^o.

Se sustituyen los datos:

b² = (15)² + (25)² – 2_*(15)_*(25) _* cos 50

b² = (225) + (625) – (750) _* 0,6427

b² = (225) + (625) – (482,025)

b² = 367,985

b = √367,985

b = 19,18 m.

Como ya se tiene el valor de los tres lados, se calcula el perímetro de ese triángulo:

P = lado a + lado b + lado c

P = 15 m + 25 m + 19, 18 m

P = 59,18 m

Ahora es posible determinar el área aplicando la fórmula de Herón, pero primero se debe calcular el semiperímetro:

sp = P ÷ 2

sp =  59,18 m ÷ 2

sp = 29,59 m.

Se sustituyen las medidas de los lados y el semiperímetro en la fórmula de Herón:

Finalmente, conociendo el área, puede ser calculada la altura relativa al lado c. A partir de la fórmula general, despejándola se tiene que:

Área = (lado _* h) ÷ 2

143,63 m² = (25 m _* h) ÷ 2

h = (2 _* 143,63 m²) ÷ 25 m

h = 287,3 m² ÷ 25 m

h = 11,5 m.

Tercer ejercicio

En el triángulo escaleno ABC el lado b mide 40 cm, el lado c mide 22 cm, y en el vértice A se forma un ángulo de 90^o. Calcular el área de ese triángulo.

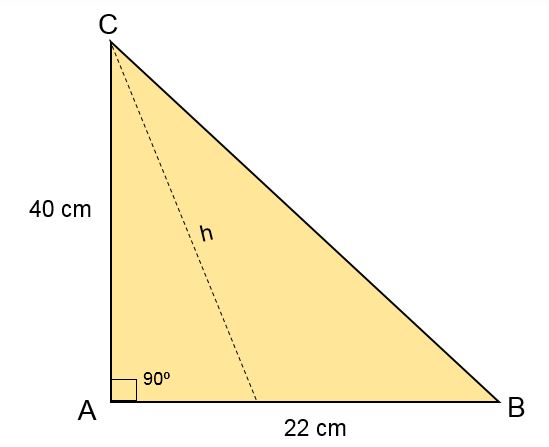
Solución

En este caso son dadas las medidas de dos lados del triángulo escaleno ABC, así como el ángulo que se forma en el vértice A.

Para determinar el área no es necesario calcular la medida del lado a, puesto que a través de las razones trigonométricas se utiliza el ángulo para hallarla.

Como se conoce el ángulo opuesto a la altura, esta será determinada por el producto de un lado y el seno del ángulo.

Sustituyendo en la fórmula del área se tiene que:

• Área = (lado _* h) ÷2
• h = c _* sen A

Área = (b _* c _* sen A) ÷ 2

Área = (40 cm _* 22 cm _* sen 90) ÷ 2

Área = (40 cm _* 22 cm _* 1) ÷ 2

Área = 880 cm² ÷ 2

Área = 440 cm².

Referencias

1. Álvaro Rendón, A. R. (2004). Dibujo Técnico: cuaderno de actividades.
2. Ángel Ruiz, H. B. (2006). Geometrías. Tecnologica de CR, .
3. Angel, A. R. (2007). Algebra Elemental. Pearson Educación,.
4. Baldor, A. (1941). Álgebra. La Habana: Cultura.
5. Barbosa, J. L. (2006). Geometria Euclidiana Plana. Rio de janeiro,.
6. Coxeter, H. (1971). Fundamentos de Geometría. México: Limusa-Wiley.
7. Daniel C. Alexander, G. M. (2014). Elementary Geometry for College Students. Cengage Learning.
8. Harpe, P. d. (2000). Topics in Geometric Group Theory. University of Chicago Press.