Triángulo equilátero: características, propiedades, fórmulas, área
Un triángulo equilátero es un polígono de tres lados, donde todos son iguales; es decir, tienen la misma medida. Por esa característica se le dio el nombre de equilátero (lados iguales).
Los triángulos son polígonos considerados como los más simples en la geometría, porque están formados tres lados, tres ángulos y tres vértices. En el caso del triángulo equilátero, por tener lados iguales, implica que sus tres ángulos también lo serán.
Índice del artículo
- 1 Características de los triángulos equilateros
- 2 Propiedades
- 3 ¿Cómo calcular el perímetro?
- 4 ¿Cómo calcular la altura?
- 5 ¿Cómo calcular los lados?
- 6 ¿Cómo calcular el área?
- 7 Ejercicios
- 8 Referencias
Los triángulos equiláteros son figuras planas y cerradas, compuestas por tres segmentos de rectas. Los triángulos son clasificados por sus características, en relación a sus lados y ángulos; el equilátero fue clasificado usando como parámetro la medida de sus lados, ya que estos son exactamente iguales, es decir, son congruentes.
El triángulo equilátero es un caso particular del triángulo isósceles debido a que dos de sus lados son congruentes. Por eso todos los triángulos equiláteros son también isósceles, pero no todos los triángulos isósceles serán equiláteros.
De esa forma los triángulos equiláteros poseen las mismas propiedades de un triángulo isósceles.
Los triángulos equiláteros también puede ser clasificados por la amplitud de sus ángulos internos como triángulo acutángulo equilátero, el cual tiene los tres lados y tres ángulos internos con la misma medida. Los ángulos serán agudos, es decir, serán menores a 90o.
Los triángulos en general poseen varias rectas y puntos que lo componen. Son utilizados para calcular el área, los lados, los ángulos, la mediana, bisectriz, la mediatriz y la altura.
- La mediana: es una recta que sale desde el punto medio de un lado y llega al vértice opuesto. Las tres medianas concurren en un punto llamado baricentro o centroide.
- La bisectriz: es una semirrecta que divide el ángulo de los vértices en dos ángulos de igual medida, por eso es conocido como eje de simetría. El triángulo equilátero posee tres ejes de simetría. En el triángulo equilátero la bisectriz se traza desde el vértice de un ángulo hasta su lado opuesto, cortándolo en su punto medio. Estas concurren en punto llamado incentro.
- La mediatriz: es un segmento perpendicular al lado del triángulo que tiene origen en la mitad de este. Existen tres mediatices en un triángulo y ellas concurren en un punto llamado circuncentro.
- La altura: es la recta que va desde el vértice hasta el lado que es opuesto y además esta recta es perpendicular a dicho lado. Todos los triángulos tienen tres alturas que coinciden en un punto llamado ortocentro.
En el siguiente gráfico observamos un triángulo escaleno donde se detallan algunos de los componentes mencionados
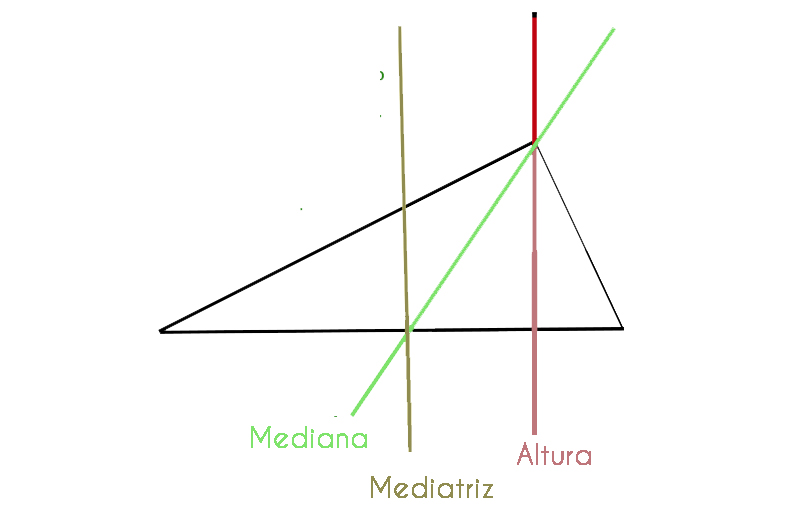
La bisectriz, la mediana y mediatriz son coincidentes
La bisectriz divide al lado de un triángulo en dos partes. En los triángulos equiláteros ese lado será dividido en dos partes exactamente iguales, es decir, el triángulo será dividido en dos triángulos rectángulos congruentes.
Así, la bisectriz trazada desde cualquier ángulo de un triángulo equilátero coincide con la mediana y la mediatriz del lado opuesto a ese ángulo.
Ejemplo:
En la siguiente figura se observa el triángulo ABC con un punto medio D que divide a uno de sus lados en dos segmentos AD y BD.
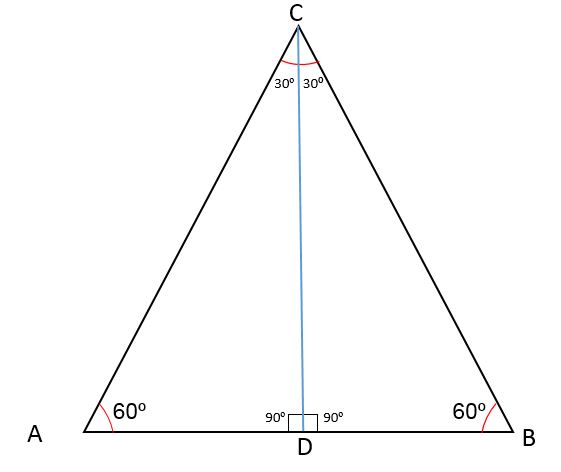
Al trazar una recta desde el punto D hasta el vértice opuesto, por definición se obtiene la mediana CD, que es relativa al vértice C y al lado AB.
Como el segmento CD divide al triangulo ABC en dos triángulos iguales CDB y CDA, significa que se tendrá el caso de congruencia: lado, ángulo, lado y por tanto CD también será la bisectriz de BCD.
Al trazar el segmento CD, se divide el ángulo del vértice en dos ángulos iguales de 30o, el ángulo del vértice A sigue midiendo 60o y la recta CD forma un ángulo de 90o con respecto al punto medio D.
El segmento CD forma ángulos que tienen la misma medida para los triángulos ADC y BDC, es decir, son suplementarios de tal forma que la medida de cada uno será:
Med. (ADB) + Med. (ADC) = 180o
2 * Med. (ADC) = 180o
Med. (ADC) =180o ÷ 2
Med. (ADC) = 90o.
Y así, se tiene que el segmento CD también es la mediatriz del lado AB.
La bisectriz y la altura son coincidentes
Al trazar la bisectriz desde el vértice de un ángulo hasta el punto medio del lado opuesto, esta divide al triángulo equilátero en dos triángulos congruentes.
De tal forma que se forma un ángulo de 90o (recto). Este indica que ese segmento de recta es totalmente perpendicular a ese lado, y por definición esa recta sería la altura.
De esa forma la bisectriz de cualquier ángulo de un triángulo equilátero, coincide con la altura relativa al lado opuesto de ese ángulo.
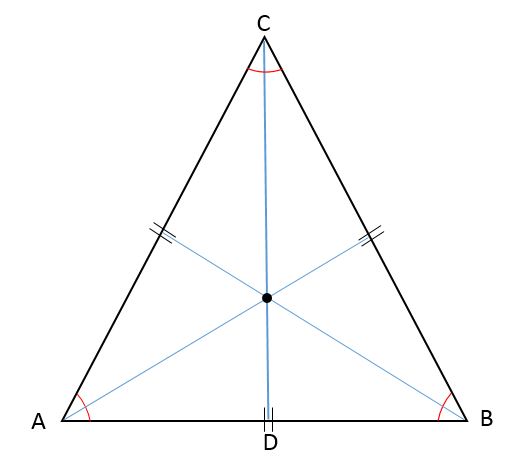
Ortocentro, baricentro, incentro y circuncentro coincidentes
Como la altura, mediana, bisectriz y mediatriz son representadas a la vez por un mismo segmento, en un triángulo equilátero los puntos de encuentro de esos segmentos -el ortocentro, baricentro, incentro y circuncentro-, se encontraran en un mismo punto:
La principal propiedad de los triángulos equiláteros, es que siempre serán triángulos isósceles, ya que los isósceles son formados por dos lados congruentes y los equiláteros por tres.
De esa forma, los triángulos equiláteros heredaron todas las propiedades del triángulo isósceles:
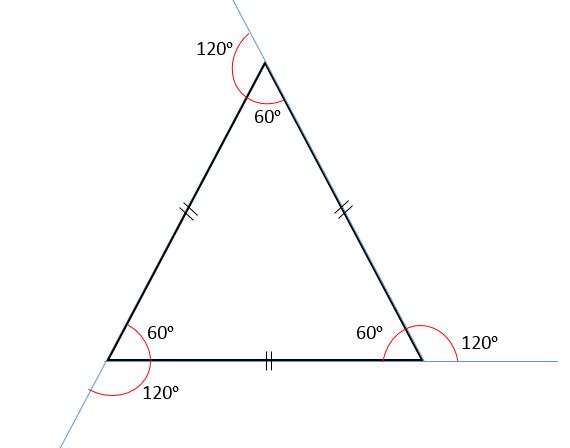
La suma de los ángulos internos es siempre igual a 180o, y como todos sus ángulos son congruentes, entonces cada uno de estos va a medir 60o.
La suma de los ángulos externos siempre será igual a 360o, por lo tanto cada ángulo externo va a medir 120o. Eso es debido a que los ángulos internos y externos son suplementares, es decir, al sumarlos siempre serán iguales a 180o.
La suma de las medidas de dos lados siempre debe ser mayor que la medida del tercer lado, es decir, a + b > c, donde a, b y c son las medidas de cada lado.
Los triángulos equiláteros tienen sus tres lados con la misma medida o longitud; es decir, son congruentes. Por lo tanto, en el item anterior se tiene que a=b=c.
Los triángulos equiláteros son conocidos también como triángulos equiángulos, porque sus tres ángulos internos son congruentes unos con otros. Esto es debido a que todos sus lados también tienen la misma medida.
El perímetro de un polígono es calculado mediante la suma de los lados. Como en este caso el triángulo equilátero tiene todos sus lados con la misma medida, su perímetro se calcula con la siguiente fórmula:
P = 3 * lado.
Como la altura es la recta perpendicular a la base, la divide en dos partes iguales al prolongarse hasta el vértice opuesto. Así son formados dos triángulos rectángulos iguales.
La altura (h) representa al cateto opuesto (a), la mitad del lado AC al cateto adyacente (b) y el lado BC representa a la hipotenusa (c).
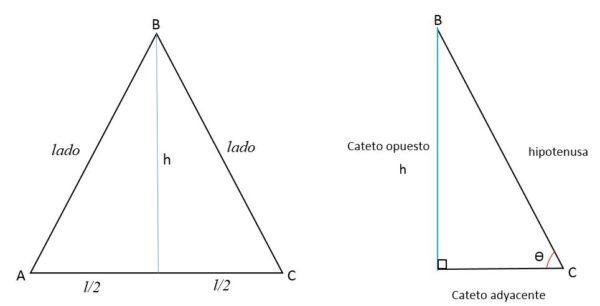
Utilizando el teorema de Pitágoras, se puede determinar el valor de la altura:
a2 + b2= c2
Donde:
a2 = altura (h).
b2 = lado b / 2.
c2 = lado a.
Sustituyendo esos valores en el teorema de Pitágoras, y despejando la altura se tiene:
h2 + ( l / 2)2 = l2
h2 + l2/ 4 = l2
h2 = l2 – l2/ 4
h2 = (4*l2 – l2) / 4
h2 = 3*l2/4
√h2 = √ (3*l2/4)
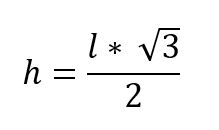
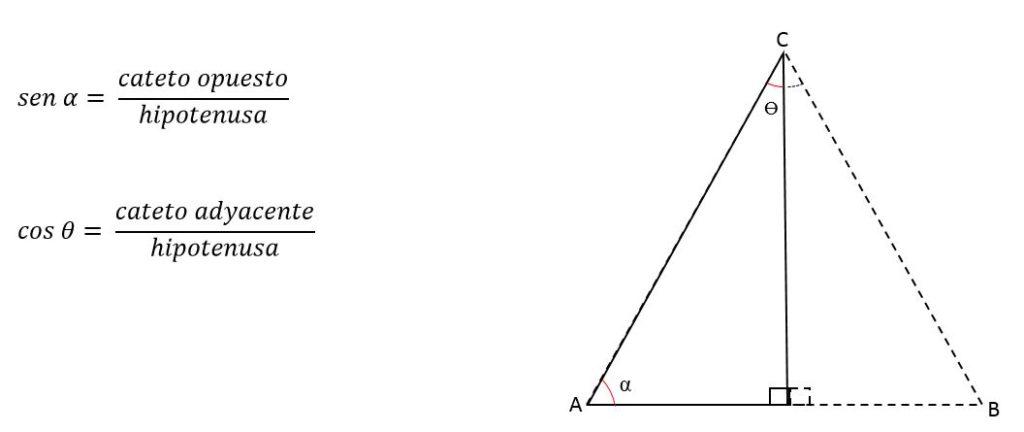
Si es conocido el ángulo que forman los lados congruentes, la altura (representada por un cateto), puede ser calculada aplicando las razones trigonométricas.
Los catetos son llamados opuestos o adyacentes dependiendo del ángulo que se tome como referencia.
Por ejemplo, en la figura anterior el cateto h será opuesto para el ángulo C, pero adyacente al ángulo B:
Así, la altura puede ser calculada con:
Existen casos donde no se conocen las medidas de los lados del triángulo, sino su altura y los ángulos que se forman en los vértices.
Para determinar el área en estos casos es necesario aplicar las razones trigonométricas.
Sabiendo el ángulo de uno de sus vértices, se identifican los catetos y se utiliza la razón trigonométrica que corresponda:
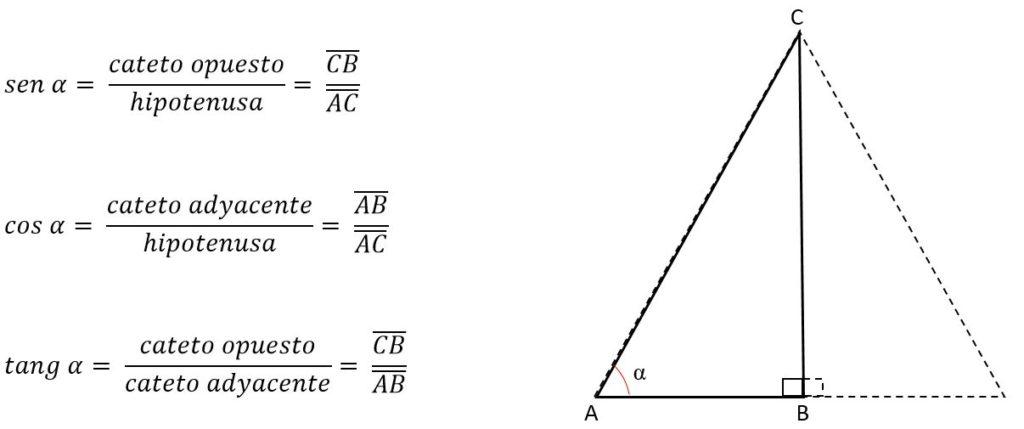
Así, el cateto AB, será opuesto para el ángulo C, pero adyacente al ángulo A. En función del lado o cateto correspondiente a la altura, se despeja el otro lado para obtener el valor de este, sabiendo que en un triángulo equilátero los tres lados siempre tendrán la misma medida.
El área de los triángulos siempre se calcula con la misma fórmula, multiplicando la base por altura y dividiendo entre dos:
Área = (b * h) ÷ 2
Sabiendo que la altura es dada por la fórmula:

Los lados de un triángulo equilátero ABC miden 20 cm cada uno. Calcular la altura y el área de ese polígono.
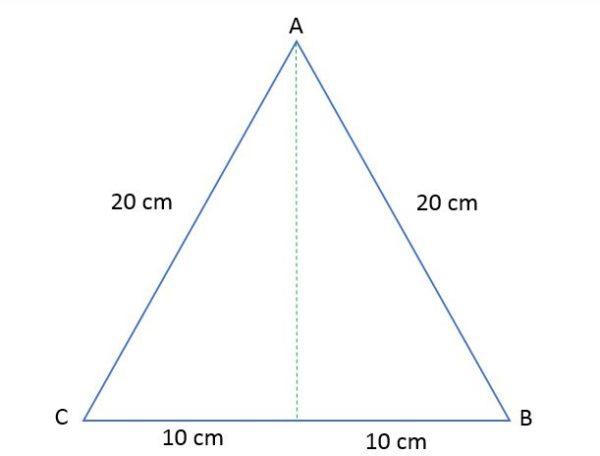
Solución
Para determinar el área de ese triángulo equilátero es necesario calcular la altura, sabiendo que al trazarla, esta divide el triángulo en dos triángulos rectángulos iguales.
De esa forma puede utilizarse el teorema de Pitágoras para hallarla:
a2 + b2= c2
Donde:
a = 20/2 = 10 cm.
b = altura.
c = 20 cm.
Se sustituyen los datos en el teorema:
102 + b2 = 202
100 cm + b2 = 400 cm
b2 = (400 – 100) cm
b2 = 300cm
b = √300 cm
b = 17,32 cm.
Es decir, que la altura del triángulo es igual a 17,32cm. Ahora es posible calcular el área del triángulo dado sustituyendo en la fórmula:
Área = (b * h) ÷ 2
Área = (20 cm * 17,32 cm) ÷ 2
Área = 346,40 cm2 ÷ 2
Área = 173,20 cm2.
Otra forma más simple de resolver el ejercicio, es sustituyendo los datos en la formula directa del área, donde también se halla implícitamente el valor de la altura:

En un terreno que tiene forma de triángulo equilátero se plantaran flores. Si el perímetro de ese terreno ese igual a 450 m, calcular la cantidad de metros cuadros que ocuparan las flores.
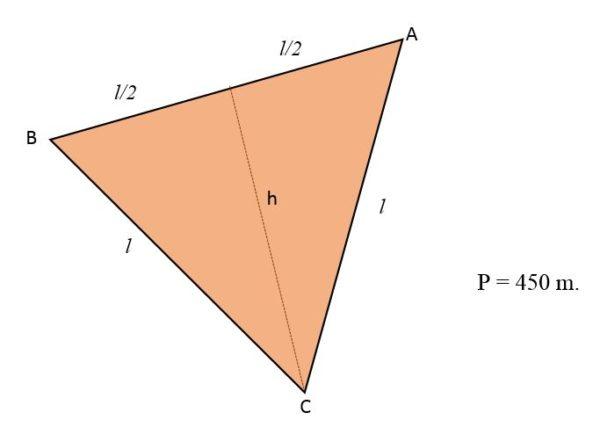
Solución
Sabiendo que el perímetro de un triángulo corresponde a la suma de sus tres lados y como el terreno tienen forma de triángulo equilátero, los tres lados de este tendrán la misma medida o longitud:
P = lado + lado + lado = 3 * l
3 * l = 450 m.
l = 450 m ÷ 3
l = 150 m.
Ahora solo es necesario calcular la altura de ese triángulo.
La altura divide al triángulo en dos triángulos rectángulos congruentes, donde uno de los catetos representa la altura y el otro la mitad de la base. Por el teorema de Pitágoras, la altura puede ser determinada:
a2 + b2= c2
Donde:
a = 150 m ÷2 = 75 m.
c = 150 m.
b = altura
Se sustituyen los datos en el teorema:
(75 m)2+ b2 = (150 m)2
5.625 m + b2 = 22.500 m
b2 = 22.500 m – 5.625 m
b2 = 16.875 m
b = √16.875 m
b = 129,90 m.
Así el área que ocuparán las flores será:
Área = b * h ÷ 2
Área = (150 m * 129,9 m) ÷ 2
Área = (19.485 m2) ÷ 2
Área = 9.742,5 m2
El triángulo equilátero ABC está dividido por un segmento de recta que va desde su vértice C hasta el punto medio D, ubicado en lado opuesto (AB). Este segmento mide 62 metros. Calcular el área y perímetro de ese triángulo equilátero.
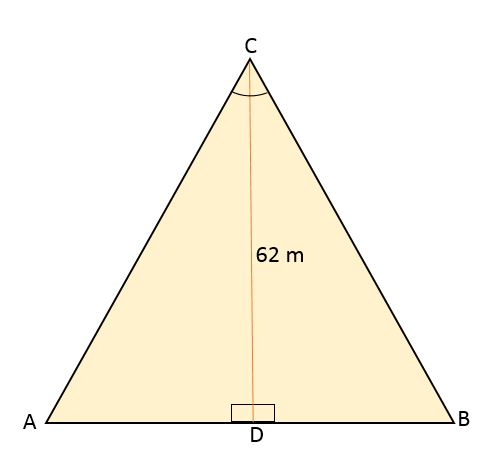
Solución
Sabiendo que el triángulo equilátero es dividido por un segmento de recta que corresponde a la altura, formando así dos triángulos rectángulos congruentes, esta a su vez también divide el ángulo del vértice C en dos ángulos con la misma medida, 30o cada uno.
La altura forma un ángulo de 90o con respecto al segmento AB, y el ángulo del vértice A medirá entonces 60o.
Entonces usando como referencia el ángulo de 30o, se establece la altura CD como cateto adyacente al ángulo y BC como hipotenusa.
A partir de esos datos puede determinarse el valor de uno de los lados del triángulo, usando las razones trigonométricas:
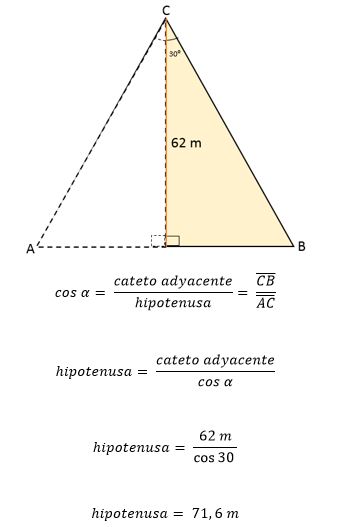
Como en el triángulo equilátero todos los lados tienen exactamente la misma medida o longitud, significa que cada lado del triángulo equilátero ABC es igual a 71,6 metros. Sabiendo eso, es posible determinar su área:
Área = b * h ÷ 2
Área = (71,6 m * 62 m) ÷ 2
Área = 4.438,6 m2 ÷ 2
Área = 2.219,3 m2
El perímetro es dado por la suma de sus tres lados:
P = lado + lado + lado = 3 * l
P = 3*l
P = 3 * 71,6 m
P = 214,8 m.
- Álvaro Rendón, A. R. (2004). Dibujo Técnico: cuaderno de actividades.
- Arthur Goodman, L. H. ( 1996). Algebra y trigonometría con geometría analítica. Pearson Educación.
- Baldor, A. (1941). Álgebra. La Habana: Cultura.
- BARBOSA, J. L. (2006). Geometria Euclidiana Plana. SBM. Rio de janeiro, .
- Coxford, A. (1971). Geometry A Transformation Approach. USA: Laidlaw Brothers.
- Euclid, R. P. (1886). Euclid’s Elements of Geometry.
- Héctor Trejo, J. S. (2006). Geometria y Trigonometria.
- León Fernández, G. S. (2007). Geometría Integrada. Instituto Tecnológico Metropolitano.
- Sullivan, J. (2006). Algebra y Trigonometria. Pearson Educación.
