Números enteros: propiedades, ejemplos, ejercicios

¿Qué son los números enteros?

Los números enteros constituyen un conjunto de números útiles para contar los objetos completos que se tienen y los que no se tienen. También para contar los que están a un lado y al otro de cierto lugar de referencia.

También con los números enteros se puede llevar a cabo la resta o diferencia entre un número y otro mayor que él, quedando asentado el resultado como una deuda, por ejemplo. La distinción entre ganancias y deudas se hacen con signos + y – respectivamente.

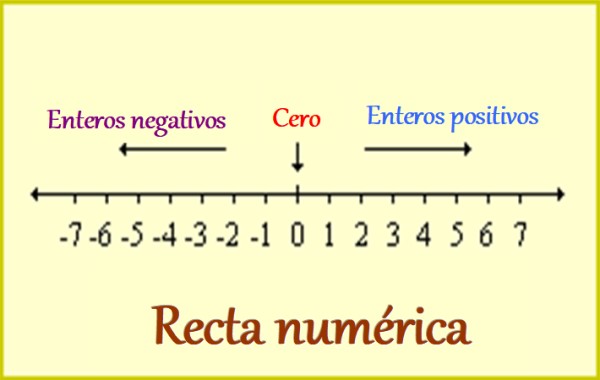
Por eso el conjunto de los números enteros incluye a los siguientes:

-Enteros positivos, que se escriben precedidos de un signo +, o simplemente sin el signo, ya que igualmente se entiende que son positivos. Por ejemplo: +1, +2, +3… y así sucesivamente.

-El 0, en el cual el signo es irrelevante, pues da lo mismo sumarlo que restarlo de alguna cantidad. Pero el 0 es muy importante, ya que es la referencia para los enteros: a un lado se ubican los positivos y al otro los negativos, como vemos en la figura superior.

-Enteros negativos, que siempre se deben escribir precedidos del signo -, ya que con ellos se distinguen las cantidades como las deudas y todas las que están al otro lado de la referencia. Ejemplos de enteros negativos son: -1, -2, -3… y de allí en adelante.

¿Cómo se representan los números enteros?

Al comienzo representamos a los números enteros con la notación de conjunto: Z = {…-4, -3, -2, -1, 0, +1, +2, +3, +4…}, es decir, listados y ordenados. Pero una representación muy útil es la que emplea la recta numérica. Para ello se requiere dibujar una recta, que por lo general es horizontal, sobre la cual se marca el 0 y se divide en tramos idénticos:

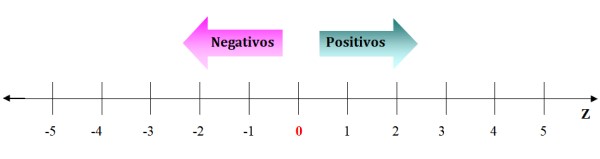
Los negativos van a la izquierda del 0 y los positivos van a la derecha. Las flechas en la recta numérica simbolizan que los números prosiguen hasta infinito. Dado un número entero cualquiera, siempre es posible encontrar uno que sea mayor u otro que sea menor.

El valor absoluto de un número entero

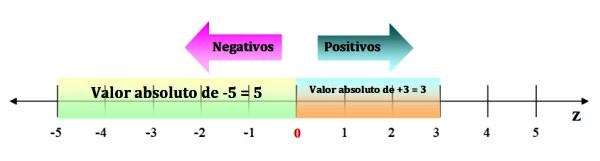
El valor absoluto de un número entero es la distancia que hay entre el número y el 0. Y las distancias siempre son positivas. Por lo tanto el valor absoluto del entero negativo es el número sin su signo menos.

Por ejemplo, el valor absoluto de -5 es 5. El valor absoluto se denota con barras, de la siguiente forma:

|-5| = 5

Para visualizarlo basta con contar los espacios en la recta numérica, desde el -5 hasta el 0. Mientras que el valor absoluto de un entero positivo es el mismo número, por ejemplo |+3| = 3, ya que su distancia al 0 es de 3 espacios:

Propiedades

-El conjunto de los números enteros se denota como Z e incluye al conjunto de los números naturales N, siendo infinitos sus elementos.

-Un número entero y el que le sigue (o el que le precede) se diferencian siempre en la unidad. Por ejemplo, después del 5 viene el 6, siendo 1 la diferencia entre ellos.

-Todo número entero tiene un predecesor y un sucesor.

-Cualquier número entero positivo es mayor que el 0.

-Un número entero negativo siempre es menor que el 0 y que cualquier número positivo. Tomemos por ejemplo el número -100, este es menor que 2, que 10 y que 50. Pero también es menor que -10, -20 y -99 y es mayor que -200.

-El 0 no tiene consideraciones de signo, ya que no es negativo ni positivo.

-Con los números enteros se pueden llevar a cabo las mismas operaciones que se realizan con los números naturales, a saber: suma, resta, multiplicación, potenciación y más.

-El entero opuesto a cierto entero x, es –x y la suma de un entero con su opuesto es 0:

x + (-x) = 0.

Operaciones con números enteros

– Suma

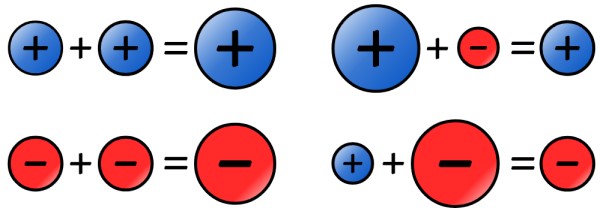
-Si los números a sumar tienen el mismo signo, se suman sus valores absolutos y al resultado se le coloca el signo que tengan los sumandos. Aquí hay algunos ejemplos:

a) (+8) + (+9) = 8 + 9 = +17

b) (-12) + (- 10) = – (12+10) = -22

-En caso de que los números sean de distinto signo, se restan los valores absolutos (el mayor del menor) y al resultado se le coloca el signo del número con mayor valor absoluto, de la siguiente forma:

a) (-8) + (21) = 21 – 8 = 13

b) (-9) + (+4) = -(9-4) = -5

Propiedades de la suma de los números enteros

-La suma es conmutativa, por lo tanto el orden de los sumandos no altera la suma. Sean a y b dos números enteros, se cumple que a+b = b+a

-El 0 es el elemento neutro de la suma de números enteros: a + 0 = a

-Cualquier número entero sumado con su opuesto es 0. El opuesto de + a es –a, y a la inversa, el opuesto de –a es +a. Por lo tanto: (+a)+ (-a) = 0.

– Resta

Para restar números enteros hay que guiarse por esta regla: la resta equivale a la suma de un número con su opuesto. Sean dos números a y b, entonces:

a – b = a + (-b)

Por ejemplo, supongamos que se necesita hacer la siguiente operación: (-3) – (+7), entonces:

(-3) – (+7) = (-3) + (-7) = – (3+7) = -10

– Multiplicación

La multiplicación de números enteros sigue ciertas reglas para los signos:

-El producto de dos números con igual signosiempre es positivo.

-Cuando se multiplican dos números de signos distintos, el resultado siempre es negativo.

-El valor del producto es igual a multiplicar los respectivos valores absolutos.

Inmediatamente algunos ejemplos que aclaran lo antes dicho:

(-5) x (+8) = – 5 x 8 = -40

(-10) x (-12) = 10 x 12 = 120

(+4) x (+32) = 4 x 32 = 128

Propiedades de la multiplicación de los números enteros

-La multiplicación es conmutativa. Sean dos números enteros a y b, se cumple que: a.b = b.a, lo que igualmente se puede expresar como:

El orden de los factores no altera el producto.

-El elemento neutro de la multiplicación es el 1. Sea a un número entero, por lo tanto a.1 = 1

-Cualquier entero multiplicado por 0 es igual a 0: a.0 = 0

La propiedad distributiva

La multiplicación cumple con la propiedad distributiva respecto de la suma. Si a, b y c son  números enteros entonces:

a.(b +c) = a.b + a.c

Seguidamente un ejemplo de cómo aplicar esta propiedad:

(-3). [(-4) + 11] = (-3).(-4)+(-3).11 = 12 – 33 = 12 + (-33) = -21

Potenciación

-Si la base es positiva, el resultado de la operación siempre es positivo.

-Cuando la base es negativa, si el exponente es par, el resultado es positivo. y si el exponente es impar, el resultado es negativo.

– División

En la división se aplican las mismas reglas de signos que en la multiplicación:

-Al dividir dos números enteros del mismo signo, el resultado siempre es positivo.

-Cuando se dividen dos enteros de signos diferentes, el cociente es negativo.

Por ejemplo:

(-12) ÷ (-4) = 3

33 ÷ (-3) = -11

Importante: la división no es conmutativa, en otras palabras a ÷ b ≠ b ÷ a y como siempre, la división entre 0 no está permitida.

– Potenciación

Sea a un número entero y queremos elevarlo a un exponente n, entonces debemos multiplicar a por sí mismo n  veces, tal como se muestra a continuación:

aⁿ = a.a.a.a. ….. .a

Además consideremos lo siguiente, tomando en cuenta que n es un número natural:

-Si a es negativo y n es par, el resultado es positivo.

-Cuando a es negativa y n es impar, da como resultado un  número negativo.

-Si a es positivo y n es par o impar, siempre resulta un entero positivo.

-Cualquier número entero elevado a la 0 es igual a 1: a⁰ = 1

-Todo número elevado a la 1 es igual al número: a¹ = a

Pongamos por ejemplo que se desea hallar (–3)⁴ , para hacerlo multiplicamos (-3) cuatro veces por sí mismo, así: (–3).(–3).(–3).(–3)= 81.

Otro ejemplo, también con un entero negativo es:

(-2)³ = (-2).(-2).(-2) = -8

Producto de potencias de igual base

Supongamos dos potencias de igual base, si las multiplicamos obtenemos otra potencia con la misma base, cuyo exponente es la suma de los exponentes dados:

aⁿ ·a^m = a^{n + m}

Cociente de potencias de igual base

Al dividir potencias de igual base, el resultado es una potencia con la misma base, cuyo exponente es la resta de los exponentes dados:

aⁿ ÷ a^m = a^{n – m}

Enseguida dos ejemplos que aclaran estos puntos:

(-2)³.(-2)⁵ = (-2) ³⁺⁵= (-2)⁸

5⁶ ÷ 5⁴ =5^6-4 = 5²

Ejemplos

Veamos ejemplos sencillos para aplicar estas reglas, recordando que en el caso de los enteros positivos, se puede prescindir del signo:

a) (+6) + (+14) = 6 + 14 = 20

b) (-8) + (- 10) = – (8 + 10) = -18

c) (-16) + (+7) = – 16 + 7 = -9

d) (+4) + (-8) + (-25) = [(+4) + (-8)] + (-25) = [4-8] -25 = -4 -25 = -29

e) (-8) – (+15) = (-8) + (-15) = -8 – 15 = -23

f) (+3) x (+9) = 3 x 9 = 27

g) (- 4) x (-11) = 4 x 11 = 44

h) (+5) x (-12) = – 5 x 12 = -60

i) (-2)³ = (-2) x (-2) x (-2) = – 8

Ejercicios resueltos

– Ejercicio 1

Una hormiga se desplaza sobre la recta numérica de la figura 1. Partiendo del punto x = +3 realiza los siguientes desplazamientos:

-Se mueve 7 unidades hacia la derecha

-Ahora se regresa 5 unidades a la izquierda

-Camina 3 unidades más hacia la izquierda.

-Se regresa y se mueve 4 unidades a la derecha.

¿En qué punto se encuentra la hormiga al finalizar el recorrido?

Solución

Llamemos D a los desplazamientos. Cuando son a la derecha se les da signo positivo y cuando son a la izquierda signo negativo. De esta manera, y partiendo de x = +3 se tiene:

-Primer D: x₁ = +3 + 7 =  +10

-Segundo D: x₂ = +10 + (-5) = +5

-Tercer D: x₃ = +5 + (-3) = +2

-Cuarto D: x₄ = +2 + 4 = +6

Cuando la hormiga termina su paseo se encuentra en la posición x = +6. Es decir, se encuentra a 6 unidades a la derecha del 0 sobre la recta numérica.

– Ejercicio 2

Resolver la siguiente operación:

{36 + [- (-4 + (-5) – 7)]}.{-[-6+5-(2+7-9)]+ 2(-8+6)]}

Solución

Esta operación contiene signos de agrupación, que son los paréntesis, los corchetes y las llaves. A la hora de resolver, hay que encargarse en primer lugar de los paréntesis, luego de los corchetes y por último de las llaves. En otras palabras, hay que trabajar desde dentro hacia afuera.

En este ejercicio, el punto representa una multiplicación, pero en caso de que entre un número y un paréntesis u otro símbolo no exista el punto, de igual manera se entiende que es un producto.

A continuación la resolución paso a paso, los colores sirven de guía para seguir el resultado de la reducción de los paréntesis, que son los símbolos de agrupación más internos:

{36 + [- (-4 + (-5) – 7)]}.{-[-6+5-(2+7-9)]+ 2(-8+6)]}=

= {36 + [- (-16)]}.{-[-6+5-(0)]+ 2(-2)]}=

= {36 + [16]}.{-[-1]- 4]}=

= {52}.{1- 4]}= {52}.{-3}= -156

– Ejercicio 3

Resolver la ecuación de primer grado:

12 + x = 30 + 3x

Solución

Se agrupan los términos con la incógnita a la izquierda de la igualdad, y los términos numéricos a la derecha:

x – 3x = 30 – 12

– 2x = 18

x = 18 / (-2)

x = – 9