Función escalonada: características, ejemplos, ejercicios
La función escalonada y = s(x) es una función definida a trozos o por partes, tal que en un intervalo finito [a,b] tiene un número finito de discontinuidades, a las cuales llamaremos x0 x1 x2 …. xn. En cada intervalo abierto (xi , xi+1), y tiene un valor constante de valor si, con discontinuidades -saltos- en los puntos xi.
La gráfica que resulta de una función como esta consiste en escalones o peldaños. Veamos un ejemplo a continuación:
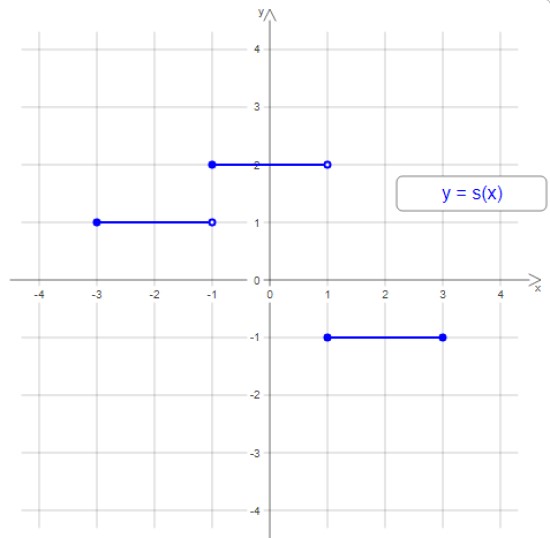
La gráfica de esta función escalonada tiene tres peldaños o intervalos escalonados, pero en general la función escalonada puede tener cualquier cantidad de escalones. La anchura de los escalones puede ser diferente y no siempre la escalera es ascendente o descendente.
La función escalonada del ejemplo se puede escribir especificando el ancho y el alto de cada escalón, así:
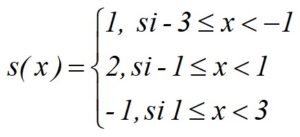
Índice del artículo
- 1 Características de la función escalonada
- 2 Ejemplos de funciones escalonadas
- 3 Ejercicios resueltos
- 4 Referencias
-La función recibe su nombre por la gráfica en forma de escalones, dados por los segmentos que la componen. Cada segmento tiene una parte del dominio de la función y en cada uno, la función es constante.
-El dominio de una función escalonada son los valores que pertenecen al intervalo para el cual se la define: [a,b], mientras que el rango lo constituyen los valores si de las alturas de los escalones.
En el ejemplo de la figura 1, el dominio es el intervalo [-3,3] y el rango son los valores -1, 1 y 2.
-La función escalonada es continua excepto en los valores que delimitan cada escalón, los puntos xi.
-Las funciones escalonadas se pueden sumar y multiplicar para dar lugar a nuevas funciones escalonadas.
-Su derivada es 0 para los puntos donde está definida, ya que en ellos la función es constante. Por su parte, la derivada no existe en las discontinuidades.
-La integral de la función escalonada s(x) entre a y b existe y corresponde a la suma de las áreas de los rectángulos de anchura xi– xi-1 y altura sk, igual a la del escalón.
Como el área de un rectángulo es el producto de la base por la altura, tenemos que:
Dentro de las funciones escalonadas hay varios tipos, por ejemplo las funciones de parte entera y la función escalón unitario, así como diversas funciones escalonadas que describen situaciones comunes, como las tarifas de muchos servicios. Veamos algunos ejemplos:
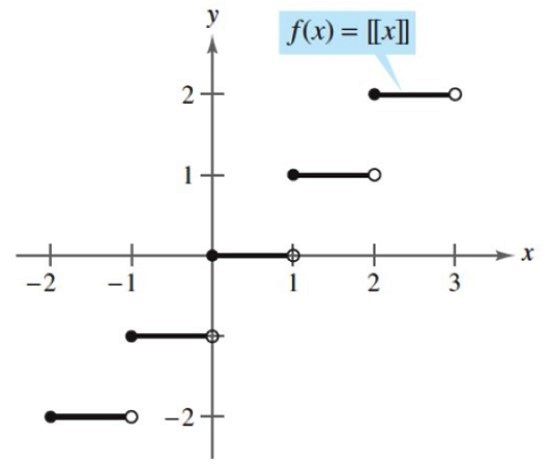
La función parte entera se denota frecuentemente usando doble corchete:
f (x) =[[x]]
Y se define como una función que asigna a cada número real el entero mayor o menor más próximo, ignorando cualquier decimal que tenga el número. Según sea el caso, tenemos:
Función techo o cielo
Asigna a cada valor del dominio el número entero más próximo por exceso. Por ejemplo:
[[+2.56]] = 3
Se ignora la parte decimal que es 0.56 y se asigna el número entero más próximo que sea mayor a 2.
Otro ejemplo:
[[–4.2]]= –3
De nuevo se omite la parte decimal 0.2 y se toma como valor de la función el entero mayor más próximo a -4, el cual es -3.
En la siguiente figura está la gráfica de la función techo, nótese que el escalón está delimitado por un pequeño círculo hueco a la izquierda y uno lleno a la derecha, ya que a cualquier número del intervalo, se le asigna al entero mayor entre los extremos del intervalo.
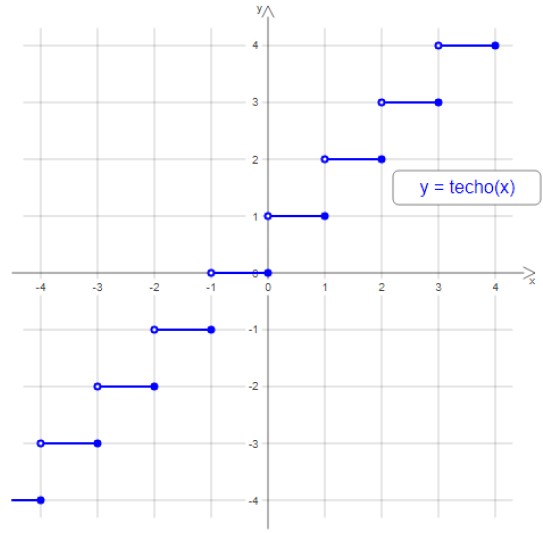
Por ejemplo, a todos los valores comprendidos entre 3 y 4 se le asigna el entero 4, a los que están comprendidos entre -2 y -1 se les asigna el -1 y así sucesivamente.
Función piso o suelo
Asigna a cada valor del dominio el número entero más próximo por defecto. Ejemplos de esta función son:
[[+3.7]] = 3
[[-1.5]] = -2
[[π]] = 3
Ambas funciones son continuas salvo para los números enteros, donde se presentan saltos, y es constante para los valores comprendidos entre los enteros k y k+1.
En una ciudad la tarifa de taxis es de 3.65 $ de base, por los primeros 100 m. Y por cada 100 m son 0.18 $, siendo el límite por recorrido de 50 km.
Se desea establecer la función que relacione el recorrido en metros con el costo del servicio en $, la cual debe tener esta forma:
f (x) = 3.65 + 0.18. [[x /100]] $
Donde la función parte entera puede ser de tipo función cielo, a la cual se añade la tarifa de base que son 3.65 $. Por ejemplo, si queremos saber cuánto se pagará por un viaje de 6.25 km = 6250 m, tendremos:
f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25 ]] $ = 15.65 $
Si la compañía de taxis escoge una función piso, entonces el cliente pagaría un poco menos por el viaje:
f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25 ]] $ = 14.65 $
Las llamadas de larga distancia entre las ciudades A y B cuestan 0.40 $ los primeros 10 minutos. Después de ese lapso, la fracción o minuto adicional vale 0.05 $.
Expresar el costo C (t) de una llamada que dure determinada cantidad de minutos.
Solución
Podemos expresar esta función si vamos analizando lo que sucede con cada opción para la duración de una llamada:
Para t ≤ 10 minutos
Cuando t, que es el tiempo que dure la llamada, sea menor o igual a 10 minutos, se pagan 0.40 $.
Por lo tanto:
f (t) = 0.40 $ para t comprendido entre 0 y 10 minutos.
Ya tenemos una parte de la función.
Para t > 10 minutos
Caso t entero
Ahora veamos lo que sucede cuando se excede el tiempo de t = 10 minutos: puede pasar que el exceso sea un número entero, por ejemplo que la conversación dure exactamente 11, 12, 13, 14 minutos o más. En ese caso el monto de la llamada será:
f (t) = 0.40 + 0.05(t-10) $, para t mayor que 10 minutos, con t entero.
Es decir que en este caso: t = 11, 12, 13, 14, 15 … minutos.
Por ejemplo, supongamos que la conversación dura exactamente 15 minutos, el costo será:
f (15) = 0.40 + 0.05(15-10) $ = 0.65 $
Caso t decimal
Por último, consideremos el caso en que la llamada dure un tiempo con parte decimal. Por ejemplo, supongamos que la llamada dure 15 minutos y 45 segundos, que en forma decimal sería 15.75 minutos.
Lo podemos expresar en términos de la función parte entera del tipo piso, suponiendo que la compañía quiere darle más beneficios al cliente, o de tipo cielo:
f (t) = 0.40 + 0.05 ⋅ [[t-9]] $
Veamos lo que el cliente pagaría si fuera una función piso:
f (15.75) = 0.40 + 0.05 ⋅ [[15.75-9]] $ = 0.40 + 0.05⋅[[6.75]] $ = 0.40 + 0.05× 6 $ = 0.70 $.
O como función cielo, en tal caso el costo sería:
f (15.75) = 0.40 + 0.05 [[15.75-9]] $ = 0.40 + 0.05⋅[[6.75]] $ = 0.40 + 0.05×7 $ = 0.75 $.
Función y gráfica
Como una función definida por partes queda:
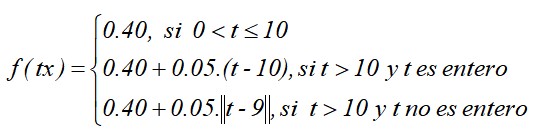
La gráfica de la función quedaría así, suponiendo que se escogió la función parte entera de tipo techo:
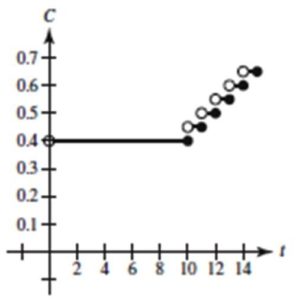
Calcular la integral ∫s(x)dx entre -3 y 3 de la función escalonada:
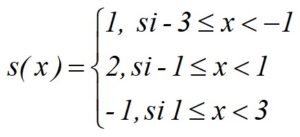
Solución
Aplicamos la definición para la integral de la función escalonada:
Por lo tanto la integral buscada I es:
I = 1. [(-1)-(-3)] + 2.[1- (-1)]+(-1).[3-1]=2+4-2 = 4
- Jiménez, R. 2006.Funciones Matemáticas. Pearson Educación.
- Larson, R. 2010. Cálculo de una variable. 9na. Edición. McGraw Hill.
- Matemáticas IV. Funciones. Recuperado de: cobaqroo.edu.mx.
- Wikipedia. Funciones de parte entera. Recuperado de: es.wikipedia.org.
- Wikipedia. Función escalonada. Recuperado de: es.wikipedia.org.
