Secciones cónicas: tipos, aplicaciones, ejemplos
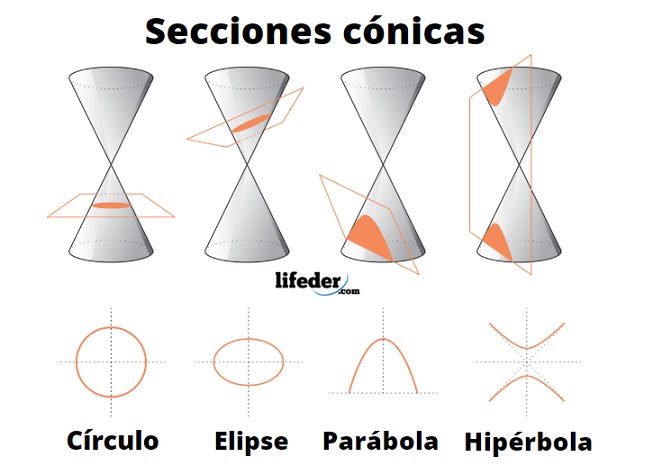
Las secciones cónicas son las curvas que se obtienen al interceptar un plano con un cono. Hay varias formas de hacer esto; por ejemplo, si el plano se hace pasar perpendicularmente al eje axial del cono se obtiene una circunferencia.
Inclinando un poco el plano respecto al eje axial del cono se obtiene una elipse, una curva que es cerrada, pero si lo inclinamos aún más se obtiene una parábola o bien una hipérbola, como se aprecia en la animación de la figura 1.
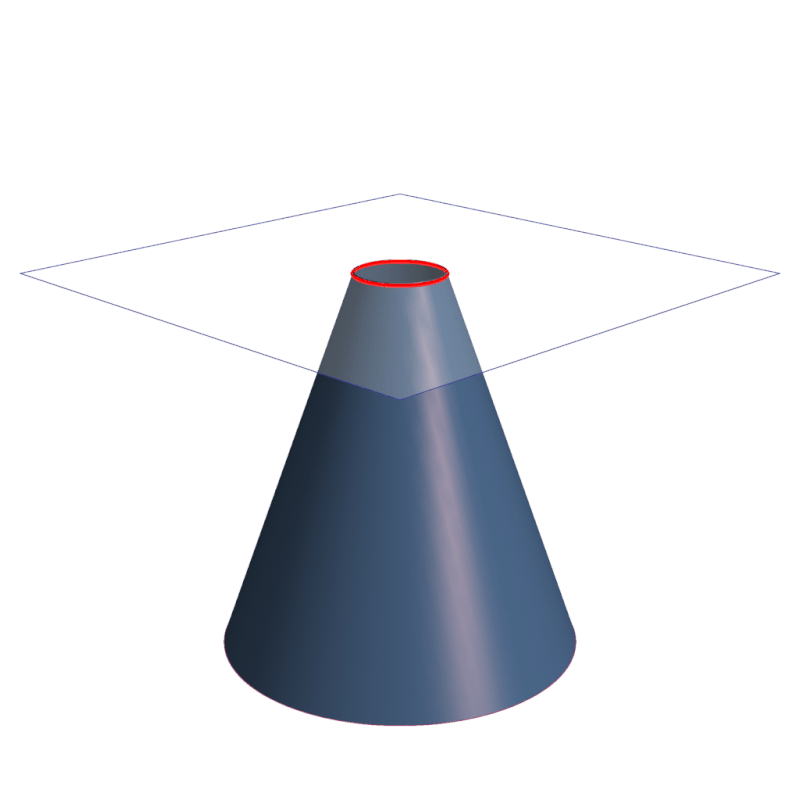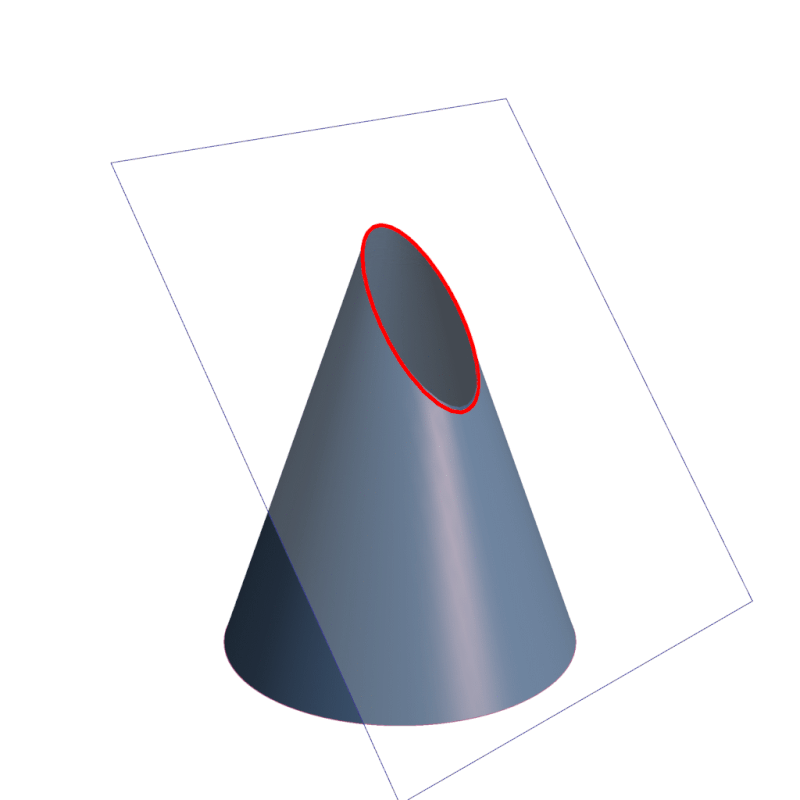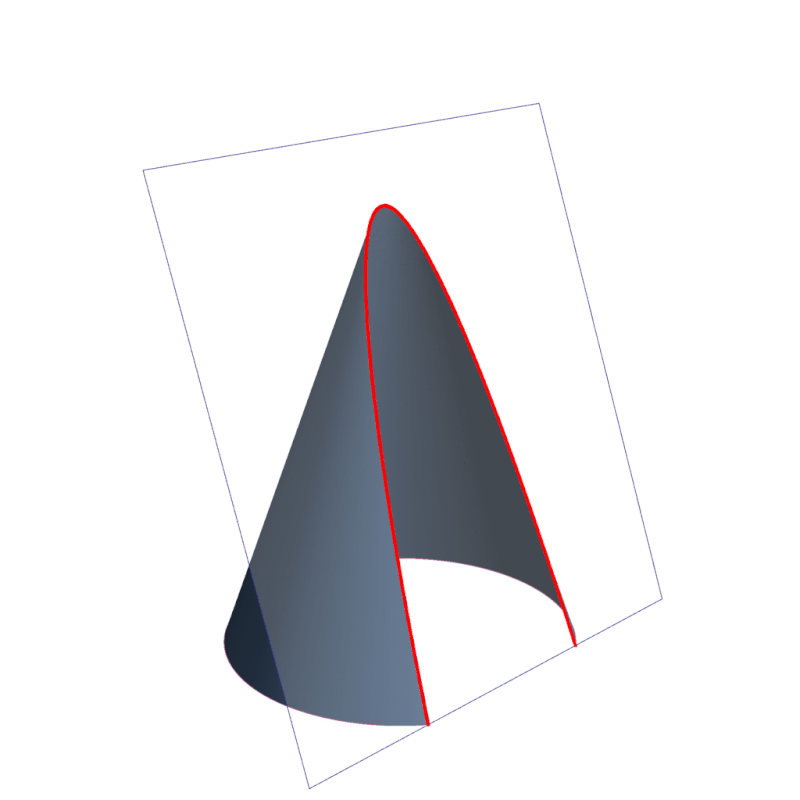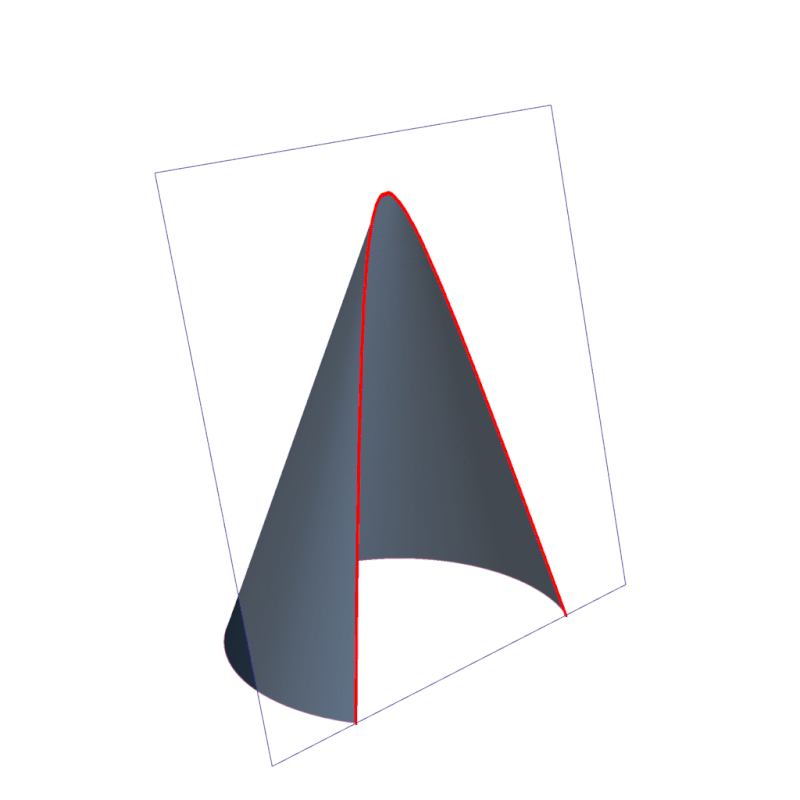
Las secciones cónicas forman parte de la naturaleza y del mundo que nos rodea. La ingeniería, la arquitectura y la astronomía son importantes ramas del saber que hacen uso de las cónicas.
Índice del artículo
Las secciones cónicas se definen como lugares geométricos que satisfacen las siguientes condiciones:
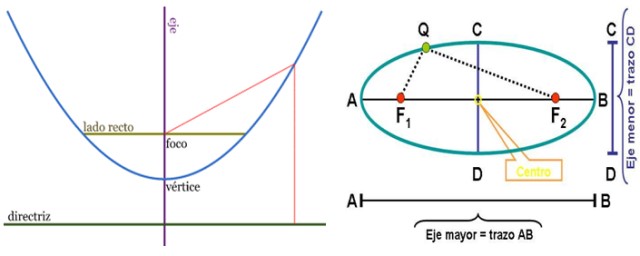
Es el lugar geométrico de todos los puntos que yacen en un plano equidistante a un punto fijo llamado foco F y a una línea recta también fija, llamada directriz.
Un punto del plano pertenece a una elipse si la suma de las distancias entre dicho punto y otros dos puntos fijos, llamados focos y ubicados sobre el eje mayor de la elipse, permanece constante.
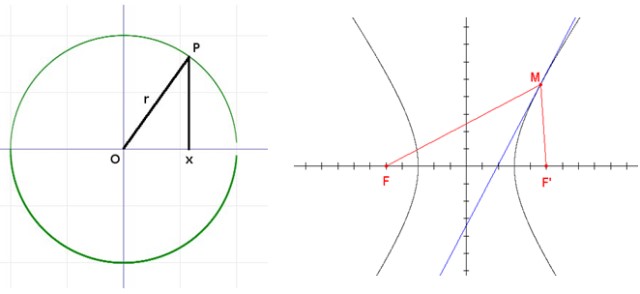
Es el lugar geométrico de todos los puntos que mantienen la misma distancia a otro punto llamado centro. Dicha distancia es el radio de la circunferencia.
Conjunto de puntos en el plano tales que la diferencia entre su distancia a dos puntos fijos llamados focos, es constante.
Veamos algunas de las aplicaciones de las secciones cónicas:
-Cuando se lanza un objeto, la trayectoria que sigue tiene forma de parábola.
-Las parábolas tienen notables aplicaciones en Ingeniería, por ejemplo en los puentes suspendidos los cables penden en forma de parábolas.
-Las parábolas también son buenas para hacer reflectores y telescopios. Esto es gracias a una interesante propiedad: al colocar una luminaria en el foco de una superficie de sección transversal parabólica, la luz viajará en rayos paralelos al eje de la parábola.
-Si los rayos luminosos paralelos al eje de simetría se acercan a la superficie parabólica, esta los concentra en el foco, circunstancia aprovechada para hacer telescopios reflectores, como el telescopio Hale de Monte Palomar.
-Los planetas del sistema solar se mueven siguiendo trayectorias elípticas, bastante cercanas a la circunferencia en el caso de los planetas mayores, la Tierra incluida. El Sol no está en el centro, sino en uno de los focos.

-La elipse se utiliza ampliamente en arquitectura como elemento decorativo y de diseño.
-Al colocar un reflector en uno de los focos de una elipse, la luz se refleja hacia el otro foco. Lo mismo sucede con el sonido. Por eso en salones con forma de elipse, quienes hablan en voz baja estando ubicados en un foco son escuchados claramente por oyentes localizados en el otro foco.
-Esta misma propiedad tiene una aplicación sorprendente en el campo de la medicina. Los cálculos renales pueden destruirse mediante sonido. Ondas de ultrasonido de gran intensidad se generan en uno de los focos de una tina elíptica llena de agua, y el paciente se ubica en el otro foco. Las ondas sonoras inciden y se reflejan en el cálculo, y con su energía lo fragmentan en pedazos pequeños, que la persona expulsa luego fácilmente durante la micción.
-Algunos cometas en el Sistema Solar siguen trayectorias hiperbólicas, siempre con el Sol en uno de los focos.
-Los focos de las hipérbolas también son muy interesantes para estudiar los fenómenos de la reflexión de ondas. Por ejemplo, al dirigir un haz de luz al foco de un espejo parabólico esta se refleja en el otro foco, una propiedad muy útil para construir telescopios, ya que la luz puede enfocarse en un espejo parabólico y ser redirigida a otro lugar más apropiado según el diseño.
-Las torres de enfriamiento de las centrales nucleares tienen silueta con forma de hipérbolas.
-Antes del advenimiento del GPS, las hipérbolas se utilizaban en navegación para ubicar embarcaciones. Las naves llevaban a bordo receptores de señales emitidas simultáneamente por las estaciones de radio A y B y una computadora se encargaba de registrar las diferencias de los tiempos de llegada de las señales, para transformarlas en diferencias de distancias. De esta forma se ubica a la nave en la rama de una hipérbola.
El procedimiento se repite con otras dos estaciones de radio C y D, que ubica a la nave en la rama de otra hipérbola. La posición definitiva de la embarcación es la intersección de ambas hipérbolas.
-La llegada de la rueda cambió el curso de la historia.
-El movimiento circular es muy común, muchas piezas giran para producir diversos efectos, desde molinos hasta ventiladores.
-Aunque las trayectorias de los planetas mayores son elípticas, las trayectorias circulares son buenas aproximaciones en muchos casos.
-Las circunferencias son elementos frecuentes en la arquitectura, el diseño, la ingeniería y la construcción. La lista de piezas con forma circular o de disco es interminable: monedas, CD’s, relojes y más.
A continuación hay dos cónicas en el plano, una circunferencia y una elipse.
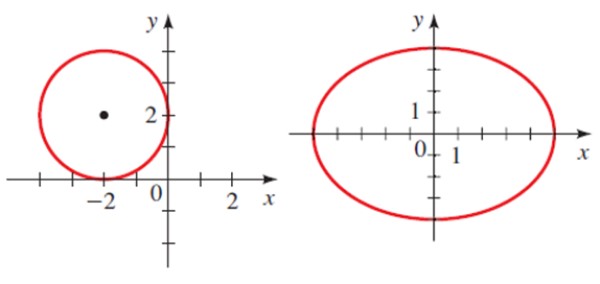
Cada una tiene una ecuación analítica:
(x-h)2 + (y-k)2 = R2
Donde h y k son las coordenadas del centro y R es el radio. Para la circunferencia mostrada en la figura la ecuación es:
(x+2)2 + (y-2)2 = 4
La ecuación de la elipse cuyo centro están el punto de coordenadas (h,k):
[(x-h)2 /a2 ]+ [(y-k)2 /b2 ]= 1
Donde a y b son los semiejes de la elipse. Para la elipse mostrada, el centro está en el punto 0,0, el semieje mayor es igual 5 y el semieje menor es 4. Por lo tanto su ecuación es:
(x2 /25 )+ (y2 / 16) = 1
- Hoffman, J. Selección de temas de Matemática. Volumen 2.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
- Wikipedia. Conic section. Recuperado de: es.wikipedia.org.
- Zill, D. 1984. Álgebra y Trigonometría. McGraw Hill.
